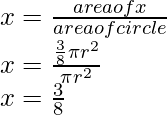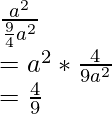Clase 10 RD Sharma Solutions – Capítulo 13 Probabilidad – Ejercicio 13.2

Pregunta 1. Suponga que deja caer un empate al azar en la región rectangular que se muestra en la fig. abajo. ¿Cuál es la probabilidad de que caiga dentro del círculo con un diámetro de 1 m?

Solución:

Área de un círculo con el radio especificado 0,5 m = (0,5) ² = 0,25 πm ²

Área del rectángulo = largo × ancho = 3 × 2 = 6m ²

$Probability = \frac{measure of specified region}{measure of whole region}$

Ahora,

La probabilidad de que la corbata caiga dentro del círculo, = área del círculo/área del rectángulo

= 0,25 π metro ² / 6 metro ²

= π /24

Por lo tanto, la probabilidad de que la corbata caiga dentro del círculo = π/24

Pregunta 2. En el diagrama adjunto, se coloca una rueda giratoria justa en el centro O del círculo. El diámetro AOB y el radio OC dividen el círculo en tres regiones denominadas X, Y y Z.? Si ∠BOC = 45°. ¿Cuál es la probabilidad de que la ruleta caiga en la región X?

Solución:

Dado,

∠BOC = 45°

Además, por la aplicación del par lineal

∠AOC = 180 – 45 = 135°

Área del círculo de radio r = πr ²

Área de la región x según la figura= θ/360 × πr ²

= 135/360 × ^πr2

= 3/8 × ^πr2

$x = \frac{area of x}{area of circle} \\ x = \frac{\frac{3}{8}\pi r^2}{\pi r^2} \\ x = \frac{3}{8}$

Por lo tanto, la probabilidad requerida de que la rueda caiga en la región X es 3/8.

Pregunta 3. En la fig. abajo consta de tres círculos concéntricos de radios, 3, 7 y 9 cm respectivamente. Se lanza un dardo y cae en el objetivo. ¿Cuál es la probabilidad de que el dardo caiga en la región sombreada?

Solución:

Ahora tenemos los siguientes valores

Circulo – con radio 3

II círculo – con radio 7

III círculo – con radio 9

Sus áreas correspondientes son:

Área del círculo = π(3) ² = 9π

Área del círculo II = π(7) ² = 49π

Área del círculo III = π(9) ² = 81π

Ahora, calculando,

Área de la región sombreada = Área del círculo II – Área del círculo I

= 49π − 9π

= 40π

Ahora, la probabilidad de que caiga en la región sombreada está dada por,

$\frac{area of shaded region}{area of third circle} \\ = \frac{40\pi}{81 \pi} \\ = \frac{40}{81}$

Por lo tanto, la probabilidad requerida de que el dardo caiga en la región sombreada es equivalente a 40/81.

Pregunta 4. En la figura, los puntos A, B, C y D son los centros de cuatro círculos que tienen cada uno un radio de una unidad de longitud. Si se selecciona al azar un punto del interior del cuadrado ABCD. ¿Cuál es la probabilidad de que el punto sea elegido de la región sombreada?

Solución:

Radio de cada uno de los círculos = 1 unidad

Por lo tanto,

lado del cuadrado ABCD = 2 unidades

Área del cuadrado ABCD = lado ² = a ² = 2 * 2 = 4 unidades cuadradas

También,

El área de cuatro cuadrantes en A,B,C y D viene dada por

= 4 * 1/4 πr ²

Sustituyendo los valores de r, obtenemos,

= π unidad cuadrada

Por lo tanto, área de la región sombreada = (4 – π) unidades cuadradas

Y, la probabilidad del punto que se selecciona de la región sombreada = (4 – π)/4 = (1 – π/4)

Pregunta 5. En la figura, JKLM es un cuadrado con lados de 6 unidades de longitud. Los puntos A y B son los puntos medios de los lados KL y LM respectivamente. Si se selecciona al azar un punto del interior del cuadrado. ¿Cuál es la probabilidad de que el punto se elija del interior de ∆JAB?

Solución:

Sabemos,

Longitud del lado cuadrado de JKLM = 6 unidades

Ahora, el área del JKLM cuadrado = 6 ² = 36 unidades cuadradas

Tenemos, A y B como los puntos medios de los lados KL y LM.

Ahora,

AL = AK = BM = BL = 3 unidades

Por lo tanto,

Área del triángulo AJK = (JK * AK) /2 = (6 * 3) / 2 = 9 unidades cuadradas

Área del triángulo JMB = (JM * MB) /2 = (6 * 3) / 2 = 9 unidades cuadradas

Área del triángulo LAB = (LA * LB) /2 = (3 * 3) / 2 = 9/2 unidades cuadradas

Suma de estas áreas = 9 + 9 + 9/2 = 45/2 unidades cuadradas.

Área del triángulo JAB = Área del cuadrado JKLM – Área de los tres triángulos

= 36 – 45/2 = 72-45/2 unidades cuadradas

= 27/2 unidades cuadradas

Probabilidad = Área del triángulo JAB/ Área del cuadrado JMLK

= 27 /(2 * 36) = 3/8

Pregunta 6. En la figura, se muestra un tablero de dardos cuadrado. La longitud de un lado del cuadrado mayor es 1,5 veces la longitud de un lado del cuadrado menor. Si se lanza un dardo y cae en el cuadrado más grande. ¿Cuál es la probabilidad de que caiga en el interior del cuadrado más pequeño?

Solución:

Supongamos que el lado del cuadrado menor es a.

Además, sea la longitud del lado del cuadrado ABCD 3/2 * a

Área del cuadrado ABCD = (3a/2) ² = 9/4 a ² unidades cuadradas

Por lo tanto,

probabilidad = $\frac{a^2}{\frac{9}{4}a^2} \\ = a^2 * \frac{4}{9a^2} \\ = \frac{4}{9}$

Publicación traducida automáticamente

Artículo escrito por mallikagupta90 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1. Suponga que deja caer un empate al azar en la región rectangular que se muestra en la fig. abajo. ¿Cuál es la probabilidad de que caiga dentro del círculo con un diámetro de 1 m?

Pregunta 2. En el diagrama adjunto, se coloca una rueda giratoria justa en el centro O del círculo. El diámetro AOB y el radio OC dividen el círculo en tres regiones denominadas X, Y y Z.? Si ∠BOC = 45°. ¿Cuál es la probabilidad de que la ruleta caiga en la región X?

Pregunta 3. En la fig. abajo consta de tres círculos concéntricos de radios, 3, 7 y 9 cm respectivamente. Se lanza un dardo y cae en el objetivo. ¿Cuál es la probabilidad de que el dardo caiga en la región sombreada?

Pregunta 4. En la figura, los puntos A, B, C y D son los centros de cuatro círculos que tienen cada uno un radio de una unidad de longitud. Si se selecciona al azar un punto del interior del cuadrado ABCD. ¿Cuál es la probabilidad de que el punto sea elegido de la región sombreada?

Pregunta 5. En la figura, JKLM es un cuadrado con lados de 6 unidades de longitud. Los puntos A y B son los puntos medios de los lados KL y LM respectivamente. Si se selecciona al azar un punto del interior del cuadrado. ¿Cuál es la probabilidad de que el punto se elija del interior de ∆JAB?

Deja una respuesta Cancelar la respuesta