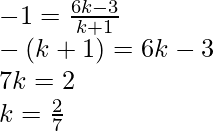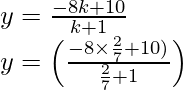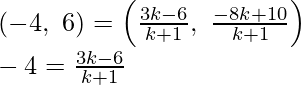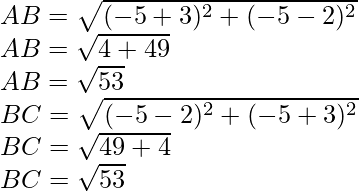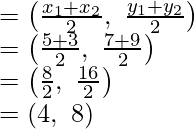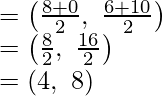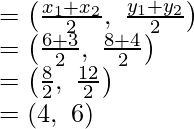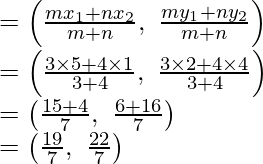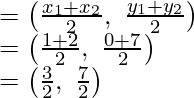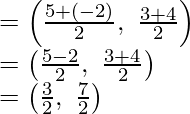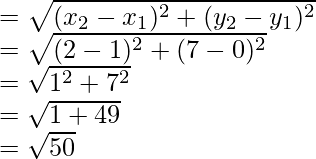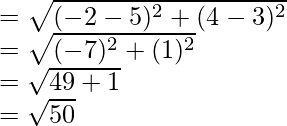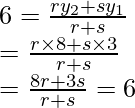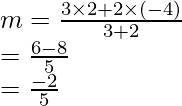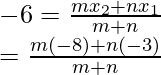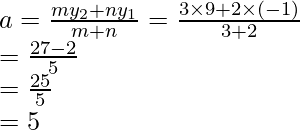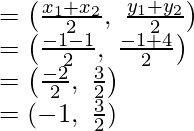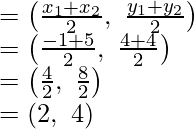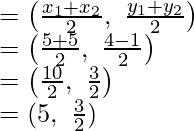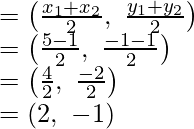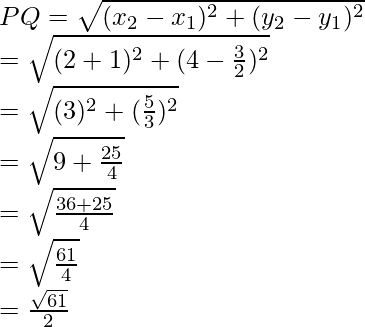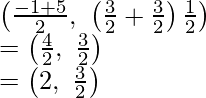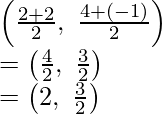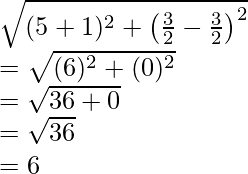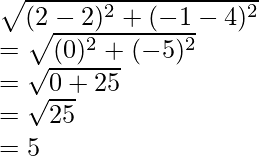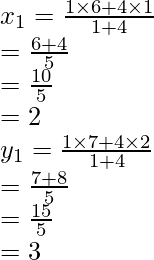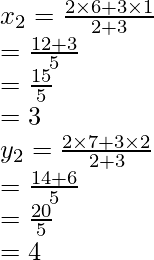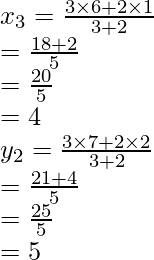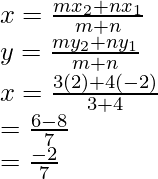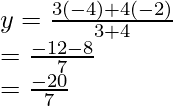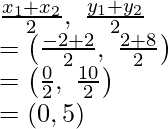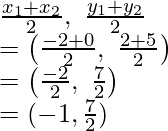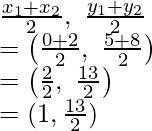Clase 10 Soluciones RD Sharma – Capítulo 14 Geometría de coordenadas – Ejercicio 14.3

Pregunta 21. Encuentra la razón en la que el punto P(-1, y) que se encuentra en el segmento de línea que une A(-3, 10) y B(6, -8) lo divide. Además, encuentra el valor de y.

Solución:

Suponga que P divide A(-3, 10) y B(6, -8) en la razón de k : 1

Dado: coordenadas de P como (-1, y)

Después de aplicar la fórmula de la sección para la coordenada x,

Obtendremos

$-1 = \frac{6k - 3}{ k + 1}\\ -(k + 1) = 6k - 3\\ 7k = 2\\ k = \frac{2}{7}$

Por lo tanto,

AB se divide por el punto P en la razón de 2 : 7

Al aplicar el valor de k, para encontrar la coordenada y

Obtendremos

$y = \frac{-8k + 10}{k + 1}\\ y = \left(\frac{-8\times\frac{2}{7} + 10)}{ \frac{2}{7} + 1}\right)$

y = (-16 + 70)/(2 + 7) = 54/9

y = 6

Por eso,

La coordenada y de P es 6.

Pregunta 22. Encuentra las coordenadas de un punto A, donde AB es el diámetro del círculo cuyo centro es (2, -3) y B es (1, 4).

Solución:

Suponga que las coordenadas del punto A sean (x, y)

Dado: AB es el diámetro,

Entonces el centro en el punto medio del diámetro

De este modo,

(2, -3) = (x + 1/ 2, y + 4/2)

2 = x + 1/2 y -3 = y + 4/2

4 = x + 1 y -6 = y + 4

x = 3 y y = -10

Por lo tanto, las coordenadas de A son (3, -10)

Pregunta 23. Si los puntos (-2, 1), (1, 0), (x, 3) y (1, y) forman un paralelogramo, encuentra los valores de x e y.

Solución:

Considere A(-2, 1), B(1, 0), C(x, 3) y D(1, y) son los puntos dados del paralelogramo.

Como sabemos que las diagonales de un paralelogramo se bisecan entre sí.

De este modo,

Coordenadas del punto medio de AC = Coordenadas del punto medio de BD

((x – 2)/2, (3 – 1)/2) = (1+1)/2, (y + 0)/2

((x – 2)/2, 1) = (1, y/2)

(x – 2)/2 = 1

x-2 = 2

x = 4

y y/2 = 1

y = 2

Por lo tanto, el valor de x es 4 y el valor de y es 2.

Pregunta 24. Los puntos A(2, 0), B(9, 1), C(11, 6) y D(4, 4) son los vértices de un cuadrilátero ABCD. Determina si ABCD es un rombo o no.

Solución:

Dado: A(2, 0), B(9, 1), C(11, 6) y D(4, 4).

El punto medio de las coordenadas AC son $(11+\frac{2}{ 2},\ 6+\frac{0}{ 2}) = (\frac{13}{2},\ 3)$

El punto medio de las coordenadas BD son $(9+\frac{4}{2},\ 1+\frac{4}{2}) = (\frac{13}{2},\ \frac{5}{2})$

Aquí,

Coordenadas del punto medio de AC ≠ Coordenadas del punto medio de BD,

ABCD no es un paralelogramo.

Por eso,

ABCD tampoco puede ser un rombo.

Pregunta 25. ¿En qué razón el punto (-4,6) divide el segmento de recta que une los puntos A(-6,10) y B(3,-8)?

Solución:

Suponga que el segmento de línea AB se divide por el punto (-4, 6) en la proporción de k : 1.

Después de aplicar la fórmula de la sección,

Obtendremos

$(-4,\ 6)=\left(\frac{3k-6}{k+1},\ \frac{-8k+10}{k+1}\right)\\ -4=\frac{3k-6}{k+1}$

-4k -4 = 3k – 6

7k = 2

k : 1 = 2 : 7

También podemos verificar la coordenada y también.

Por eso,

La razón en que el segmento de recta AB se divide por el punto (-4,6) es 2 : 7.

Pregunta 26. Halla la razón en que el eje y divide el segmento de recta que une los puntos (5, -6) y (-1, -4). Además, encuentre las coordenadas del punto de división.

Solución:

Suponga que P(5, -6) y Q(-1, -4) son los puntos dados.

Considere que el segmento de línea PQ está dividido por el eje y en la relación k : 1.

Después de aplicar la fórmula de sección para la coordenada x (ya que es cero)

Obtendremos,

$\frac{-k+5}{k+1}=0$

-k + 5 = 0

k = 5

Por lo tanto,

La razón en la que el eje y divide los 2 puntos dados es 5 : 1

Ahora más, para encontrar las coordenadas del punto de división

Al poner k = 5, obtendremos

$\left(\frac{-5+5}{5+1},\ \frac{-4\times5-6}{5+1}\right)=\left(0,\ \frac{-13}{3}\right)$

Por lo tanto,

Las coordenadas del punto de división son (0, -13/3)

Pregunta 27. Muestre que A(-3, 2), B(-5, 5), C(2, -3) y D(4, 4) son los vértices de un rombo.

Solución:

Dado: A(-3, 2), B(-5, 5), C(2, -3) y D(4, 4)

Más lejos,

El punto medio de las coordenadas AC son $\left(-3+\frac{2}{ 2},\ 2\ -\ \frac{3}{ 2}\right) = \left(\frac{-1}{2},\ \frac{-1}{2}\right)$

Y,

El punto medio de las coordenadas BD son $\left(-5+\frac{4}{ 2},\ -5+ \frac{4}{ 2}\right) = \left(\frac{-1}{2},\ \frac{-1}{2}\right)$

Por lo tanto,

El punto medio de ambas diagonales es el mismo.

De este modo,

ABCD es un paralelogramo.

Ahora,

para los lados

$AB=\sqrt{(-5+3)^2+(-5-2)^2}\\ AB=\sqrt{4+49}\\ AB=\sqrt{53}\\ BC=\sqrt{(-5-2)^2+(-5+3)^2}\\ BC=\sqrt{49+4}\\ BC=\sqrt{53}$

AB = BC

Podemos ver que ABCD es un paralelogramo con lados adyacentes iguales.

Por lo tanto,

ABCD es un rombo.

Pregunta 28. Encuentra las longitudes de las medianas de un ΔABC que tiene vértices en A(0, -1), B(2, 1) y C(0, 3).

Solución:

Suponga que AD, BE y CF son las medianas de ΔABC

Ahora,

Las coordenadas de D son $\left(2+\frac{0}{ 2},\ 1+\frac{3}{2}\right)$ = (1, 2)

Las coordenadas de E son $\left(\frac{0}{2},\ 3-\frac{1}{ 2}\right)$ = (0, 1)

Las coordenadas de F son $\left(2+\frac{0}{2},\ 1-\frac{1}{2}\right)$ = (1, 0)

Más lejos,

La longitud de las medianas

Longitud de la mediana AD = $\sqrt{(1-0)^2+(2+1)^2}$ = √10 unidades

Longitud de la mediana BE = $\sqrt{(2-0)^2+(1-1)^2}$ = 2 unidades

Longitud de la mediana CF = $\sqrt{(1-0)^2+(0-3)^2}$ = = √10 unidades

Pregunta 29. Encuentra las longitudes de la mediana de un ΔABC que tiene vértices en A(5, 1), B(1, 5) y C(-3, -1).

Solución:

Dado: Vértices de ΔABC como A(5, 1), B(1, 5) y C(-3, -1).

Considere AD, BE y CF como las medianas

Las coordenadas de D son $\left(1-\frac{3}{ 2},\ 5-\frac{1}{2}\right)$ = (-1, 2)

Las coordenadas de E son $\left(5-\frac{3}{ 2},\ 1-\frac{1}{2}\right)$ = (1, 0)

Las coordenadas de F son $\left(5+\frac{1}{ 2},\ 1+\frac{5}{2}\right)$ = (3, 3)

Más lejos,

La longitud de las medianas

Longitud de la mediana AD = $\sqrt{(5+1)^2+(1-2)^2}$ = √37 unidades

Longitud de la mediana BE = $\sqrt{(1-1)^2+(5-0)^2}$ = 5 unidades

Longitud de la mediana CF = $\sqrt{(3+3)^2+(3+1)^2}$ = √52 unidades

Pregunta 30. Halla las coordenadas del punto que divide el segmento de recta que une los puntos (-4, 0) y (0, 6) en cuatro partes iguales.

Solución:

Considere A(-4, 0) y B(0, 6) ya que son los puntos dados

Y,

Supongamos que P, Q y R son los puntos que dividen a AB en cuatro puntos iguales, como se muestra en la fig.

De este modo,

Como sabemos que AP : PB = 1 : 3

Aplicando la fórmula de la sección las coordenadas de P son

$\left(\frac{1\times0+3(-4)}{1+3},\ \frac{1\times6+3\times0}{1+3}\right)=\left(-3,\ \frac{3}{2}\right)$

Y,

Podemos ver que Q es el punto medio de AB

Por lo tanto, las coordenadas de Q son

$\left(\frac{-4+0}{2},\ \frac{0+6}{2}\right)=(-2, 3)$

Finalmente,

La relación de AR : BR es 3 : 1

Entonces, después de aplicar la fórmula de la sección, las coordenadas de R son

$\left(\frac{3\times0+1\times(-4)}{3+1},\ \frac{3\times6+1\times0}{3+1}\right)=\left(-1,\ \frac{9}{2}\right)$

$=\left(\frac{x_1+x_2}{2},\ \frac{y_1+y_2}{2}\right)\\ =\left(\frac{5+3}{2},\ \frac{7+9}{2}\right)\\ =\left(\frac{8}{2},\ \frac{16}{2}\right)\\ =(4,\ 8)$

$=\left(\frac{8+0}{2},\ \frac{6+10}{2}\right)\\ =\left(\frac{8}{2},\ \frac{16}{2}\right)\\ =(4,\ 8)$

Por lo tanto, esto es lo mismo que el primer caso.

$=\left(\frac{x_1+x_2}{2},\ \frac{y_1+y_2}{2}\right)\\ =\left(\frac{6+3}{2},\ \frac{8+4}{2}\right)\\ =\left(\frac{8}{2},\ \frac{12}{2}\right)\\ =(4,\ 6)$

$=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ =\sqrt{(1-4)^2+(2-6)^2}\\ =\sqrt{(-3)^2+(-4)^2}\\ =\sqrt{9+16}\\ =\sqrt{25}$ = 5 unidades

$\frac{AP}{BP}=\frac{3}{4}$

$=\left(\frac{mx_1+nx_2}{m+n},\ \frac{my_1+ny_2}{m+n}\right)\\ =\left(\frac{3\times5+4\times1}{3+4},\ \frac{3\times2+4\times4}{3+4}\right)\\ =\left(\frac{15+4}{7},\ \frac{6+16}{7}\right)\\ =\left(\frac{19}{7},\ \frac{22}{7}\right)$

,

$=\left(\frac{x_1+x_2}{2},\ \frac{y_1+y_2}{2}\right)\\ =\left(\frac{1+2}{2},\ \frac{0+7}{2}\right)\\ =\left(\frac{3}{2},\ \frac{7}{2}\right)$

$=\left(\frac{5+(-2)}{2},\ \frac{3+4}{2}\right)\\ =\left(\frac{5-2}{2},\ \frac{3+4}{2}\right)\\ =\left(\frac{3}{2},\ \frac{7}{2}\right)$

Ahora, la longitud de AC

$=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ =\sqrt{(2-1)^2+(7-0)^2}\\ =\sqrt{1^2+7^2}\\ =\sqrt{1+49}\\ =\sqrt{50}$

y longitud de BD = $=\sqrt{(-2-5)^2+(4-3)^2}\\ =\sqrt{(-7)^2+(1)^2}\\ =\sqrt{49+1}\\ =\sqrt{50}$

Podemos ver que AC = BD

Por lo tanto, ABCD es un rectángulo.

,

$m=\frac{rx_2+sx_1}{r+s}$

y $6=\frac{ry_2+sy_1}{r+s}\\ =\frac{r\times8+s\times3}{r+s}\\ =\frac{8r+3s}{r+s}=6$

$⇒ \frac{r}{s}=\frac{3}{2}$

La relación es 3 : 2

$m=\frac{3\times2+2\times(-4)}{3+2}\\ =\frac{6-8}{5}\\ =\frac{-2}{5}$

,

$-6=\frac{mx_2+nx_1}{m+n}\\ =\frac{m(-8)+n(-3)}{m+n}$

-6 = (-8m -3n)/(m + n)

-6m – 6n = -8m – 3n

8m – 6m = 6n – 3n

2m = 3n

m/n = 3/2

$a=\frac{my_2+ny_1}{m+n}=\frac{3\times9+2\times(-1)}{3+2}\\ =\frac{27-2}{5}\\ =\frac{25}{5}\\ =5$

,,,

$=\left(\frac{x_1+x_2}{2},\ \frac{y_1+y_2}{2}\right)\\ =\left(\frac{-1-1}{2},\ \frac{-1+4}{2}\right)\\ =\left(\frac{-2}{2},\ \frac{3}{2}\right)\\ =(-1,\ \frac{3}{2})$

$=\left(\frac{x_1+x_2}{2},\ \frac{y_1+y_2}{2}\right)\\ =\left(\frac{-1+5}{2},\ \frac{4+4}{2}\right)\\ =\left(\frac{4}{2},\ \frac{8}{2}\right)\\ =(2,\ 4)$

$=\left(\frac{x_1+x_2}{2},\ \frac{y_1+y_2}{2}\right)\\ =\left(\frac{5+5}{2},\ \frac{4-1}{2}\right)\\ =\left(\frac{10}{2},\ \frac{3}{2}\right)\\ =(5,\ \frac{3}{2})$

$=\left(\frac{x_1+x_2}{2},\ \frac{y_1+y_2}{2}\right)\\ =\left(\frac{5-1}{2},\ \frac{-1-1}{2}\right)\\ =\left(\frac{4}{2},\ \frac{-2}{2}\right)\\ =(2,\ -1)$

$PQ=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ =\sqrt{(2+1)^2+(4-\frac{3}{2})^2}\\ =\sqrt{(3)^2+(\frac{5}{3})^2}\\ =\sqrt{9+\frac{25}{4}}\\ =\sqrt{\frac{36+25}{4}}\\ =\sqrt{\frac{61}{4}}\\ =\frac{\sqrt{61}}{2}$

$\left(\frac{-1+5}{2},\ \left(\frac{3}{2}+\frac{3}{2}\right)\frac{1}{2}\right)\\ =\left(\frac{4}{2},\ \frac{3}{2}\right)\\ =\left(2,\ \frac{3}{2}\right)$

$\left(\frac{2+2}{2},\ \frac{4+(-1)}{2}\right)\\ =\left(\frac{4}{2},\ \frac{3}{2}\right)\\ =\left(2,\ \frac{3}{2}\right)$

Entonces puede ser un cuadrado o un rombo.

Ahora longitud de PR = $\sqrt{(5+1)^2+\left(\frac{3}{2}-\frac{3}{2}\right)^2}\\ =\sqrt{(6)^2+(0)^2}\\ =\sqrt{36+0}\\ =\sqrt{36}\\ =6$

Y la longitud del sistema operativo

$\sqrt{(2-2)^2+(-1-4)^2}\\ =\sqrt{(0)^2+(-5)^2}\\ =\sqrt{0+25}\\ =\sqrt{25}\\ =5$

porque las diagonales no son iguales

Por lo tanto, PQRS es un rombo.

,,

$x=\frac{m_1x_2+m_2x_1}{m_1+m_2}$

⇒ P divide a AB en razón 1 : 4

$x_1=\frac{1\times6+4\times1}{1+4}\\ =\frac{6+4}{5}\\ =\frac{10}{5}\\ =2\\ y_1=\frac{1\times7+4\times2}{1+4}\\ =\frac{7+8}{5}\\ =\frac{15}{5}\\ =3$

Por lo tanto, las coordenadas de P son (2, 3)

⇒ Q divide a AB en la razón 2 : 3

$x_2=\frac{2\times6+3\times1}{2+3}\\ =\frac{12+3}{5}\\ =\frac{15}{5}\\ =3\\ y_2=\frac{2\times7+3\times2}{2+3}\\ =\frac{14+6}{5}\\ =\frac{20}{5}\\ =4$

Por lo tanto, Coordenadas de 3, 4

⇒ R divide a AB en razón 3 : 2

Por lo tanto,

$x_3=\frac{3\times6+2\times1}{3+2}\\ =\frac{18+2}{5}\\ =\frac{20}{5}\\ =4\\ y_2=\frac{3\times7+2\times2}{3+2}\\ =\frac{21+4}{5}\\ =\frac{25}{5}\\ =5$

Por lo tanto, las coordenadas de R son (4, 5).

coordenadascoordenadas

AP = 3/7 AB

7AP = 3AB

7AP = 3(AP + BP)

⇒ 7 PA = 3 PA + 3 PA

⇒ 7 PA – 3 PA = 3 PA

⇒ 4 PH = 3 PB

$\frac{AP}{BP}=\frac{3}{4}$

Por lo tanto,

AP : BP = 3 : 4

Porque P divide a AB en la razón de 3 : 4 cuyos extremos son A(-2, -2) y B(2, -4)

Por lo tanto, las coordenadas de P serán

$x=\frac{mx_2+nx_1}{m+n}\\ y=\frac{my_2+ny_1}{m+n}\\ x=\frac{3(2)+4(-2)}{3+4}\\ =\frac{6-8}{7}\\ =\frac{-2}{7}$

$\\ y=\frac{3(-4)+4(-2)}{3+4}\\ =\frac{-12-8}{7}\\ =\frac{-20}{7}$

Por lo tanto,

Las coordenadas de P serán $\left(\frac{-2}{7},\ \frac{-20}{7}\right)$

coordenadas

Suponga que P, Q y R dividen el segmento de línea AB en cuatro partes iguales

Las coordenadas de A son (-2, 2) y de B son (2, 8)

Las coordenadas de Q serán:

$\frac{x_1+x_2}{2},\ \frac{y_1+y_2}{2}\\ =\left(\frac{-2+2}{2},\ \frac{2+8}{2}\right)\\ =\left(\frac{0}{2},\ \frac{10}{2}\right)\\ =(0, 5)$

Del mismo modo, las coordenadas de P serán:

$\frac{x_1+x_2}{2},\ \frac{y_1+y_2}{2}\\ =\left(\frac{-2+0}{2},\ \frac{2+5}{2}\right)\\ =\left(\frac{-2}{2},\ \frac{7}{2}\right)\\ =(-1, \frac{7}{2})$

Las coordenadas de R serán:

$\frac{x_1+x_2}{2},\ \frac{y_1+y_2}{2}\\ =\left(\frac{0+2}{2},\ \frac{5+8}{2}\right)\\ =\left(\frac{2}{2},\ \frac{13}{2}\right)\\ =(1, \frac{13}{2})$

Por lo tanto, las coordenadas de P son (1, 7/2)

Las coordenadas de Q son (0, 5)

Las coordenadas de R son (1, 13/2)

Publicación traducida automáticamente

Artículo escrito por yashchuahan y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 10 Soluciones RD Sharma – Capítulo 14 Geometría de coordenadas – Ejercicio 14.3 | conjunto 2

Pregunta 21. Encuentra la razón en la que el punto P(-1, y) que se encuentra en el segmento de línea que une A(-3, 10) y B(6, -8) lo divide. Además, encuentra el valor de y.

Pregunta 22. Encuentra las coordenadas de un punto A, donde AB es el diámetro del círculo cuyo centro es (2, -3) y B es (1, 4).

Pregunta 23. Si los puntos (-2, 1), (1, 0), (x, 3) y (1, y) forman un paralelogramo, encuentra los valores de x e y.

Pregunta 24. Los puntos A(2, 0), B(9, 1), C(11, 6) y D(4, 4) son los vértices de un cuadrilátero ABCD. Determina si ABCD es un rombo o no.

Pregunta 25. ¿En qué razón el punto (-4,6) divide el segmento de recta que une los puntos A(-6,10) y B(3,-8)?

Pregunta 26. Halla la razón en que el eje y divide el segmento de recta que une los puntos (5, -6) y (-1, -4). Además, encuentre las coordenadas del punto de división.

Pregunta 27. Muestre que A(-3, 2), B(-5, 5), C(2, -3) y D(4, 4) son los vértices de un rombo.

Pregunta 28. Encuentra las longitudes de las medianas de un ΔABC que tiene vértices en A(0, -1), B(2, 1) y C(0, 3).

Pregunta 29. Encuentra las longitudes de la mediana de un ΔABC que tiene vértices en A(5, 1), B(1, 5) y C(-3, -1).

Pregunta 30. Halla las coordenadas del punto que divide el segmento de recta que une los puntos (-4, 0) y (0, 6) en cuatro partes iguales.

$\frac{AP}{BP}=\frac{3}{4}$

,

,

,

,,,

,,

coordenadascoordenadas

coordenadas

Deja una respuesta Cancelar la respuesta