Sean las coordenadas de tres vértices A (-2, -1), B (1, 0) y C (4, 3)
Y que las diagonales AC y BD se bisequen en O
Por lo tanto, las coordenadas de O serán
Por lo tanto(1 + x)/2 = 1
1 + x = 2
X = 1
Por tanto, las coordenadas de D serán (1, 2).
Suponga que los bordes de una diagonal AC de un paralelogramo ABCD son A (3, -4) y C (-6, 2)
Considere que AC y BD se bisecan en O.
Por lo tanto,
El punto medio de AC será
Suponga que el cuarto vértice del paralelogramo sea (x, y)
Por lo tanto,
El punto medio de BD será
-1 + x = -3
x = -2
y
(-3 + y)/2 = -1
-3 + y = -2
y = -2 + 3 = 1
Por lo tanto, las coordenadas de D son (-2, 1).
,
1 1 2 2 3 3
Por lo tanto,
x2 + x3 = 2
y 2 + y 3 = 2
De manera similar, E es el punto medio de AC
Por lo tanto,
x 3 + x 1 = 4
y 3 + y 1 = -6
Y
F es el punto medio de AB
Por lo tanto,
x2 + x1 = 6
y 2 + y 1 = 8
Ahora,
Al sumar obtendremos
Al restar (ii), (iii) e (i) de (iv), obtenemos
Similarmente
Al sumar obtendremos
Al restar (vi), (vii) y (v) de (viii), obtenemos
Por tanto, los vértices de ∆ABC son A (4, 0), B(2, 8), C(0, -6)
y
Este punto (x, y) se encuentra en la línea en la línea x – y – 2 = 0
Por lo tanto, la relación = 2 : 3 internamente
Si O es el punto medio de AC, entonces sus coordenadas serán
y
Si O es el punto medio de BD, entonces las coordenadas serán
x + 2a + b = 2a
x = 2a – 2a – b = -b
y
y + 2a – b = 2a
y = 2a – 2a + b = b
Por lo tanto, las coordenadas de D serán (-b, b).
Suponga que las coordenadas de C sean (x 1 , y 1 ) y de D sean (x 2 , y 2 )
Si O es el punto medio de AC, entonces
3 + x 1 = 4
x1 = 4 – 3 = 1
y
y
2 + y 1 = -10
y 1 = -10 – 2 = -12
Por lo tanto, las coordenadas de C serán (1, -12)
Nuevamente, si O es el punto medio de BD, entonces
-1 + x2 = 4
x2 = 4 + 1 = 5
y
y2 = -10
Por tanto, las coordenadas de D serán (5, -10).
coordenadas,
Las coordenadas de los puntos medios de los lados BC, CA y AB son D (3, 4), E (4, 6) y F (5, 7) del ∆ABC.
Suponga que las coordenadas de los vértices del triángulo son
Ahora las coordenadas de D serán
x2 + x3 = 6
y
y 2 + y 3 = 4
y 2 + y 3 = 8
De manera similar, las coordenadas de E serán
x 3 + x 1 = 8
y
y
y 1 + y 2 = 14
Ahora,
x2 + x3 = 6 …….(i)
x 3 + x 1 = 8 ……..(ii)
x1 + x2 = 10 ……..(iii)
Al sumar obtendremos
2(x1 + x2 + x3 ) = 24
Al restar cada uno de (iv),
Obtendremos
x 1 = 6, x 2 = 4 y x 3 = 2
Similarmente,
y 2 + y 3 = 8 ……..(v)
y 3 + y 1 = 12 ………(vi)
y 1 + y 2 = 14 ……..(vii)
Al sumar, obtendremos
2(y1 + y2 + y3 ) = 34
Al restar cada uno de (viii),
Obtendremos
y 1 = 9
y 2 = 5
y 3 = 3
Por lo tanto, las coordenadas serán de A (6, 9), B (4, 5) y C (2, 3)
Dos puntos A y B trisecan el segmento de línea que une los puntos P (3, 3) y Q (6, -6) y A está más cerca de P y A también se encuentra en la línea 2x + y + k = 0
Ahora,
A divide el segmento de recta PQ en la razón de 1 : 2
es decir,
PA = AQ = 1 : 2
Suponga que las coordenadas de A son (x, y), luego
Las coordenadas de A son (4, 0)
Como A se encuentra en la recta 2x + y + k = 0
Por eso,
lo satisfará
2
8 + k = 0
k = -8
,
A (1, -2), B (3, 6) y C (5, 10) son los tres vértices consecutivos del paralelogramo ABCD
Supongamos que (x, y) es su cuarto vértice
AC y BD son sus diagonales que se bisecan en O
Como O es el punto medio de AC
Por lo tanto,
Las coordenadas de O serán
Al comparar,
3 + x = 3
3 + x = 6
x = 3
y
(6 + y)/2 = 4
6 + y = 8
y = 2
Por lo tanto, las coordenadas del cuarto vértice D son (3, 2).
,
A (a, -11), B (5, b), C (2, 15) y D (1, 1) son los vértices de un paralelogramo ABCD
Las diagonales AC y BD se bisecan en O
Como O es el punto medio de AC
Por lo tanto,
Las coordenadas de O serán
De manera similar, O es el punto medio de BD también
Por lo tanto,
Las coordenadas de O serán
(2 + a)/2 = 3
segundo + 1 = 4
segundo = 3
Por eso,
un = 4
segundo = 3
,coordenadas
Por lo tanto,
Al sumar obtenemos
Al restar de (iv) obtenemos
x3 = -4
y
y 2 + y 3 = -4 …….(v)
y 3 + y 1 = 2 …….(vi)
y1 + y2 = -6 ………(vii)
Al sumar, obtendremos
Al restar de (viii)
y 3 = 2
Por lo tanto, las coordenadas de A son (-2, 0) de B son (10, -6) y de C (-4, 2).
Suponga que la línea AB cuyos extremos son A (3, -4) y B (1, 2)
Ahora,
Como P divide a AB en la razón 1 : 2
Por lo tanto,
Las coordenadas de P serán
De manera similar, Q divide a AB en la razón 2 : 1
p = 7/3, q = 0
puntos
Los puntos A (2, 1) y B (5, -8) son los extremos del segmento AB
Los puntos P y Q lo trisecan y P se encuentra en la línea 2x – y + k = 0
Como P divide a AB en la razón de 1 : 2
Por lo tanto,
Las coordenadas de P serán
Por lo tanto,
Las coordenadas de P son (3, -2)
Como se encuentra en 2x – y + k = 0
Por lo tanto,
lo satisfará
2 × 3 – (-2) + k = 0
⇒ 6 + 2 + k = 0
⇒ 8 + k = 0
⇒ k = -8
,
En ∆ABC, las coordenadas de A (4, 2) de (6, 5) y de (1, 4) y AD es BE y CF son las medianas
tales que D, E y F son los puntos medios de los lados BC, CA y AB respectivamente
P es un punto en AD tal que AP : PD = 2 : 1
Ahora las coordenadas de D serán
(ii) Como P divide a AD en la razón de 2 : 3
Por lo tanto,
Las coordenadas de P serán
De este modo,
Las coordenadas de P son
(iii) Como E y F son el punto medio si CA y AB respectivamente
Las coordenadas de E serán
y de F será
Como Q y R dividen BE y CF de tal manera que BQ : QE = 2 : 1 y CR : RF = 2 : 1
Por lo tanto,
Las coordenadas de Q serán
es decir, Q 1 es (11/3, 11/3)
y de manera similar las coordenadas de R serán
R es (11/3, 11/3)
(iv) Podemos ver que las coordenadas de P, Q y R son las mismas
es decir, P, Q y R coinciden entre sí.
Las medianas de los lados de un triángulo pasan por el mismo punto que se llama baricentro del triángulo.
,
Las diagonales de un paralelogramo se bisecan
O es el punto medio de AC y también de BD
O es el punto medio de AC
Por lo tanto,
Las coordenadas de O serán
⇒ 8 + k = 15
⇒ k = 15 – 8 = 7
y
⇒ 2 + p = 5
⇒ p = 5 – 2 = 3
Por eso,
k = 7, pag = 3
El punto P divide el segmento de recta uniendo los puntos A (3, -5) y B (-4, 8)
⇒ AP : PB = k : 1
Suponga que las coordenadas de P sean (x, y), entonces
Como x + y = 0
Por lo tanto,
4k – 2 = 0
4k = 2
k = 2/4
k = 1/2
puntos
P es el punto medio del segmento de línea que une los puntos A (-10, 4) y B (-2, 0)
Las coordenadas de P serán
P miente en CD también,
⇒ 10 = 3y – 8x
⇒ 3y = 10 + 8 = 18
⇒ y = 18/3 = 6
⇒ y = 6
Como sabemos que si un punto (x, y) divide el segmento de recta que une
Ahora aquí, C (-1, 2) divide el segmento de línea que une A (2, 5) y B (x, y) en la proporción de 3: 4
Ahora,
⇒ 3x + 8 = -7
y
⇒ 20 – 3 años = 14
⇒ x = -5
y
⇒ y = 2
Ahora,
1 1 2 2 , 3 3 1 2 3 1 2 , 3
Suponga que las coordenadas de D sean (x, y). Sabemos que las diagonales de un paralelogramo se bisecan entre sí.
Por eso,
Punto medio de AC = Punto medio de BD
Por lo tanto, las coordenadas de D son
1 1 2 2 , 3 3
1 1 2 2 3 3
Sabemos que la mediana biseca el segmento de línea en dos partes iguales, es decir, aquí D es el punto medio de BC.
Por lo tanto,
Coordenadas del punto medio de BC =
re =
Supongamos que las coordenadas de un punto P sean (x, y)
Dado que, el punto P (x, y), dividir la recta que une A (x 1, y 1 ) y
D
en la ración de 2 : 1,
Entonces las coordenadas de P
Usando la fórmula de la sección interna, obtenemos
Por lo tanto,
Coordenadas requeridas de los puntos P =
Supongamos que las coordenadas de un punto Q sean (p, q)
Dado: El punto Q (p, q) divide la recta que une B(x 2, y 2 ) y E
En la proporción de 2 : 1
Entonces las coordenadas de Q
BE es la mediana del lado CA. Entonces, BE divide AC en dos partes iguales]
Por lo tanto,
Punto medio de AC = Coordenadas de E
Entonces, la coordenada requerida del punto Q
Ahora, consideremos que las coordenadas de un punto E sean (α, β).
Se da que, el punto R (α, β), divide la recta que une C (x 3 , y 3 ) y
F
en la ración 2 : 1,
Entonces, las coordenadas de R ser
Aquí, CF es la mediana del lado AB, por lo que CF divide a AB en dos partes iguales
Por eso,
Punto medio de AB = Coordenadas de CF
Entonces, la coordenada requerida del punto R
Coordenada del baricentro del ∆ABC = (suma de abscisas de todos los vértices/3, suma de todos los vértices/2)
Publicación traducida automáticamente
Artículo escrito por yashchuahan y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

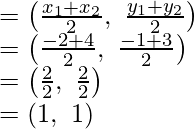
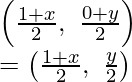

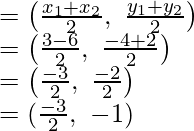
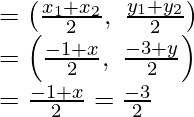

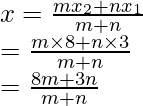
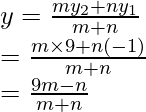

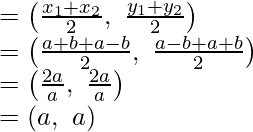
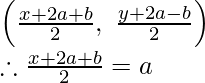


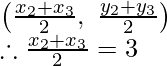
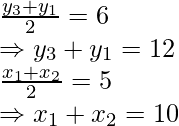

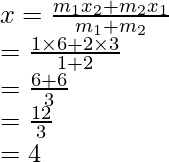
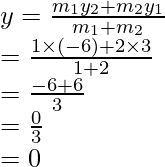


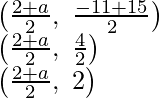

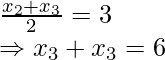
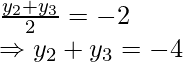
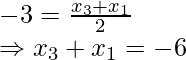
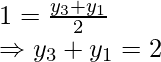
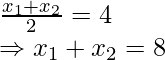
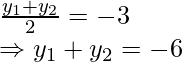

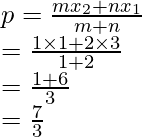
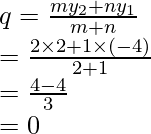

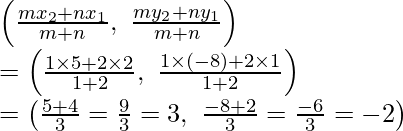

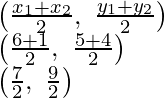
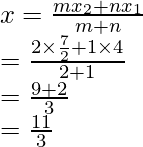
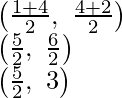
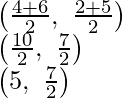
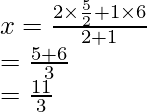
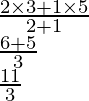
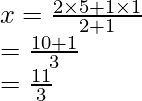
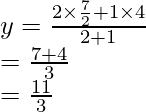

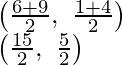
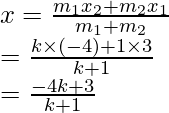
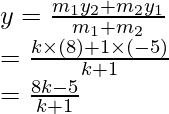
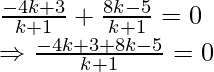
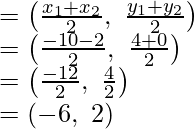
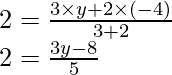

![Rendered by QuickLaTeX.com =\left[\frac{2\left(\frac{x_2+x_3}{2}\right)+1.x_1}{2+1},\ \frac{2\left(\frac{y_2+y_3}{2}\right)+1.y_1}{2+1}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5559f20fc7bc55e2d64a06efbddcf672_l3.png)


![Rendered by QuickLaTeX.com =\left[\frac{2\left(\frac{x_1+x_3}{2}\right)+1.x_2}{2+1},\ \frac{2\left(\frac{y_1+y_3}{2}\right)+1.y_2}{2+1}\right]\\ \left(\frac{x_2+x_3+x_1}{3},\ \frac{y_2+y_3+y_1}{3}\right)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ceb17107b0896af61e06f9a9f5902439_l3.png)
![Rendered by QuickLaTeX.com =\left[\frac{2\left(\frac{x_1+x_2}{2}\right)+1.x_3}{2+1},\ \frac{2\left(\frac{y_1+y_2}{2}\right)+1.y_3}{2+1}\right]\\ \left(\frac{x_2+x_3+x_1}{3},\ \frac{y_2+y_3+y_1}{3}\right)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2eebab6864f4ea04173b66c24a708aed_l3.png)