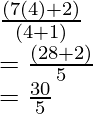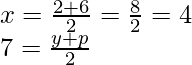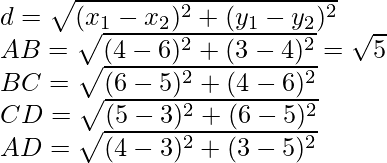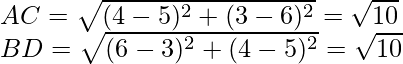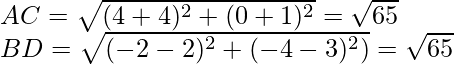Pregunta 1. Encuentra las coordenadas del punto que divide el segmento de recta que une (-1, 3) y (4, – 7) internamente en la razón 3:4.
Solución:
Suponga que P(x, y) sea el punto necesario.
Después de aplicar la fórmula de la sección,
Como sabemos que aquí las coordenadas son
Ahora aquí tenemos,
x1 = – 1
y 1 = 3
× 2 = 4
y 2 = -7
metro : norte = 3 : 4
De este modo,
Por eso,
Las coordenadas de P son (8/7, -9/7)
Pregunta 2. Encuentra los puntos de trisección del segmento de línea que une los puntos:
(i) (5, – 6) y (-7, 5)
(ii) (3, – 2) y (-3, – 4)
(iii) (2, – 2) y (-7, 4)
Solución:
(i) Suponga que P y Q son los puntos de trisección para AB
De este modo,
AP = PQ = QB
De este modo,
P divide a AB dentro en la razón de 1 : 2,
Después de poner la fórmula de la sección,
Las coordenadas de P son

Después de este,
Q también divide a AB dentro en la razón de 2:1.
Por lo tanto, sus coordenadas son
(ii) Suponga que P y Q son los puntos de trisección de AB, es decir, AP = PQ = QB
Así, P divide a AB dentro en la razón de 1:2.
Por lo tanto, después de poner en la fórmula de la sección,
Las coordenadas de P son
Después de este,
Q también divide como dentro en la proporción de 2: 1
Por lo tanto, las coordenadas de Q se muestran como
(iii) Suponga que P y Q son los puntos de la trisección de AB
es decir, AP = PQ = OQ
Como, P divide a AB dentro en la razón 1 : 2.
Así, las coordenadas de P, al poner en la fórmula de la sección, se muestran como
Después de este,
Q también divide a AB poniendo la razón 2:1.
Por lo tanto, las coordenadas de Q se muestran como
Pregunta 3. Encuentra las coordenadas del punto donde se unen las diagonales del paralelogramo formado al unir los puntos (-2, -1), (1, 0), (4, 3) y (1, 2).
Solución:

Suponga: A(-2, -1), B(1, 0), C(4, 3) y D(1, 2) son los puntos dados.
Suponga que P(x, y) es el punto de intersección de las diagonales de la
paralelogramo formado por los puntos dados. como se muestra en la figura.
Como sabemos, las diagonales de un paralelogramo se bisecan entre sí.
Por eso,
Las coordenadas de P son (1, 1).
Pregunta 4. Demuestra que los puntos (3, 2), (4, 0), (6, -3) y (5, -5) son los vértices de un paralelogramo.
Solución:

Suponga: A(3, -2), B(4, 0), C(6, -3) y D(5, -5)
Suponga que P(x, y) es el punto de intersección de las diagonales AC y BD de ABCD. Como se muestra en la figura.
Ahora, el punto medio de AC se muestra como,
Punto medio de AC
Ahora nuevamente, el punto medio de BD se muestra como,
Por lo tanto, suponga que las diagonales AC y BD se bisecan entre sí.
Además, como sabemos que las diagonales de un paralelogramo se bisecan entre sí.
Por eso,
ABCD es un paralelogramo.
Pregunta 5. Si P(9a – 2, -b) divide el segmento de recta que une A(3a + 1, -3) y B(8a, 5) en la razón 3 : 1, encuentra los valores de a y b.
Solución:
Dado: P(9a – 2, -b) divide el segmento de recta que une A(3a + 1, -3) y B(8a, 5) en la razón 3 : 1
Después de aplicar la fórmula de sección
Las coordenadas de P son
Y,
Ahora, resolvamos para a, tendremos
(9a – 2) × 4 = 24a + 3a + 1
36a – 8 = 27a + 1
9a = 9
un = 1
Ahora, resolvamos para b, tendremos
4x-b = 15-3
-4b = 12
b = -3
Por eso,
Los valores de a y b son 1 y -3 respectivamente.
Pregunta 6. Si (a, b) es el punto medio del segmento de línea que une los puntos A (10, -6), B(k, 4) y a – 2b = 18, encuentre el valor de k y el distancia AB.
Solución:
Dado: (a, b) es el punto medio del segmento de recta A(10, -6) y B(k, 4)
De este modo,
(a, b) =
a =
y b = -1
2a = 10 + k
k = 2a – 10
Dado, a – 2b = 18
Aplicando b = -1 arriba obtendremos,
a-2(-1) = 18
a = 18 – 2 = 16
Ya que,
k = 2(16) – 10 = 32 – 10 = 22
Por lo tanto,
AB =
= 2√61 unidades
Pregunta 7. Halla la razón en que el punto (2, y) divide el segmento de recta que une los puntos A(-2, 2) y B(3, 7). Además, encuentra el valor de y.
Solución:
Supongamos: El punto P(2, y) divide el segmento de recta que une los puntos A(-2, 2) y B(3, 7) en la razón k : 1
Así, las coordenadas de P estarán dadas por
Además, dadas las coordenadas de P son (2, y)
Asi que,
Así, resolviendo para k, obtendremos
2(k + 1) = (3k – 2)
2k + 2 = 3k – 2
k = 4
Ahora usa el valor de k para encontrar y,
tenemos
y =
y = 6
Por eso,
La razón 4 : 1 y y = 6
Pregunta 8. Si A(-1, 3), B(1, -1) y C(5, 1) son los vértices de un triángulo ABC, encuentra la longitud de la mediana que pasa por A.
Solución:

Suponga que AD es la mediana a través de A.
Tal que, AD es la mediana, D es el punto medio de BC
De este modo,
Las coordenadas de D
son = (3 , 0)
Por lo tanto,
La longitud de la mediana AD =
= 5 unidades
Pregunta 9. Si los puntos P, Q(x, 7), R, S(6, y) en este orden dividen el segmento de recta que une A(2, p) y B (7, 10) en 5 partes iguales, hallar x, y, y pág.
Solución:

Dado: AP = PQ = QR = RS = SB
Ya que,
Q es el punto medio de A y S
Después,
y + p = 14 ….. (i)
De este modo,
Como S divide a QB en la razón 2 : 1
= 9
Por lo tanto,
p = 14 – 9 = 5
Por eso,
x = 4,
y = 9
y
pag = 5
Pregunta 10. Si un vértice de un triángulo es (1, 1) y los puntos medios de los lados que lo atraviesan son (-2, 3) y (5, 2), encuentra los otros vértices.
Solución:
Suponga que A(1, 1) es el vértice dado y
D(-2, 3), E(5, 2) sean los puntos medios de AB y AC
Entonces, D y E son los puntos medios de AB y AC
x 1 + 1 = 4
x1 = -5
y 1 + 1 = 6
y 1 = 5
Así, las coordenadas de B son (-5, 5)
Ahora,
x2 + 1 = 10
× 2 = 9
y 2 + 1 = 4
y 2 = 3
Por eso,
Las coordenadas de C son (9, 3)
Por eso,
Los otros vértices del triángulo son (-5, 5) y (9, 3).
Pregunta 11 (i). ¿En qué razón el segmento que une los puntos (-2, -3) y (3, 7) se divide por el eje y? Además, encuentre las coordenadas del punto de división.
Solución:
Suponga que P(-2, -3) y Q(9, 3) son los puntos dados.
Suponga que el eje y divide PQ en la relación k : 1 en R(0, y)
Por lo tanto, las coordenadas de R se muestran por
Después, equiparando
= 0
3k – 2 = 0
k = 2/3
Por eso,
La relación es 2 : 3
Después de poner k = 2/3 en las coordenadas de R, obtendremos
R (0, 1)
Pregunta 11 (ii). ¿En qué razón se divide el segmento de recta que une (-3, -1) y (-8, -9) en el punto (-5, -21/5)?
Solución:
Suponga que A(-3, -1) y B(-8, -9) son los puntos dados.
Y,
Supongamos que P es el punto que dividirá a AB en la razón de k : 1
Por lo tanto, las coordenadas de P se pueden mostrar por
Por lo tanto, dadas las coordenadas de P
Después de igualar, obtendremos
-8k – 3 = -5k – 5
3k = 2
k = 2/3
Por tanto, el punto P divide a AB en la razón 2 : 3
Pregunta 12. Si el punto medio de la línea que une (3, 4) y (k, 7) es (x, y) y 2x + 2y + 1 = 0 encuentra el valor de k.
Solución:
Como (x, y) es el punto medio
x = (3 + k)/2 y y = (4 + 7)/2 = 11/2
Dado: El punto medio se encuentra en la línea 2x + 2y + 1 = 0
3 + k + 11 + 1 = 0
Por lo tanto,
k = -15
Pregunta 13. Halla la razón en que el punto P(3/4, 5/12) divide los segmentos de recta que unen el punto A(1/2, 3/2) y B(2, -5).
Solución:
Dado: Puntos A(
) y B(2, -5)
Asuma el punto P(
) y divida el segmento de línea AB en la razón de k : 1
Así, como sabemos que
Por tanto, igualaremos la abscisa que obtendremos;
3(k + 1) = 4(2k + 1/2)
3k + 3 = 8k + 2
5k = 1
k = 1/5
Por eso,
El punto P(
) se divide en razón de 1 : 5.
Pregunta 14. Halla la razón en que la recta que une (-2, -3) y (5, 6) se divide por
(i) eje x
(ii) eje y
Además, encuentre las coordenadas del punto de división en cada caso.
Solución:
Suponga que A(-2, -3) y B(5, 6) son los puntos dados.
(i) Suponga que el eje x divide a AB en la razón k : 1 en el punto P.
Por lo tanto, las coordenadas del punto de división se muestran como,
Por lo tanto, P se encuentra en el eje x,
La coordenada y es cero.
Por lo tanto,
6k – 3 = 0
k = 1/2
Por lo tanto,
La relación requerida es 1 : 2
Aplicando valor de k en las coordenadas de P
vamos a conseguir, p
(ii) Suponga que el eje y divide a AB en la proporción de k : 1 en el punto Q.
Por lo tanto, las coordenadas del punto de división se muestran como,
Por lo tanto, Q se encuentra en el eje y,
La ordenada x es cero.
Por lo tanto,
Por lo tanto,
La relación requerida es 2: 5
Aplicando el valor k en las coordenadas de Q
Obtendremos, Q
Pregunta 15. Demuestra que los puntos (4, 5), (7, 6), (6, 3), (3, 2) son los vértices de un paralelogramo. ¿Es un rectángulo?
Solución:

Suponga que A (4, 5), B (7, 6), C (6, 3) y D (3, 2) son los puntos dados, como se muestra en la figura
Y,
Sea el punto P el punto de intersección de AC y BD.
El punto medio de las coordenadas AC son
= (5, 4)
El punto medio de las coordenadas BD son
= (5, 4)
Por lo tanto, podemos ver que el punto medio de AC y BD es el mismo.
Por eso,
ABCD es un paralelogramo.
Ahora,
CA =
= √8 unidades
y,
BD =
= √32 unidades
Por lo tanto,
CA ≠ BD
Por lo tanto, ABCD no es un rectángulo.
Pregunta 16. Demuestra que (4, 3), (6, 4), (5, 6) y (3, 5) son los puntos angulares de un cuadrado.
Solución:

Suponga que A(4, 3), B(6, 4), C(5, 6) y D(3, 5) son los puntos dados, como se muestra en la figura.
Aplicando la fórmula de distancia:
Podemos ver que la longitud de todos los lados es la misma.
Ahora,
La longitud de las diagonales son;
La longitud de ambas diagonales es la misma.
Por tanto, podemos decir que los puntos dados son los puntos angulares de un cuadrado.
Pregunta 17. Demuestra que los puntos (-4, -1), (-2, -4), (4, 0) y (2, 3) son los vértices de un rectángulo.
Solución:

Suponga que A(-4, -1), B(-2, -4), C(4, 0) y D(2, 3) son los puntos dados.
Ahora,
El punto medio de las coordenadas AC son
El punto medio de las coordenadas BD son
Por eso,
Podemos ver que AC y BD tienen el mismo punto.
Y,
ahora las diagonales
Por lo tanto, la longitud de las diagonales también es la misma.
Por lo tanto, los puntos dados son los vértices de un rectángulo.
Pregunta 18. Encuentra la longitud de las medianas de un triángulo cuyos vértices son A(-1, 3), B(1, -1) y C(5, 1).
Solución:

Suponga que AD, BF y CE son las medianas de ΔABC
Las coordenadas de D son
= (3, 0)
Las coordenadas de E son
= (0, 1)
Las coordenadas de F son
= (2, 2)
Ahora,
Obteniendo la longitud de las medianas respectivamente:
Longitud de AD =
= 5 unidades
Longitud de BF =
= 10 unidades
Longitud de CE =
= 5 unidades
Pregunta 19. Halla la razón en que el segmento de recta que une los puntos A (3, -3) y B (-2, 7) se divide por el eje x. Además, encuentre las coordenadas del punto de división.
Solución:
Suponga que el punto en el eje x sea (x, 0). {y – la coordenada es cero}
Y,
Permita que este punto divida el segmento de recta AB en la razón de k : 1.
Después de aplicar la fórmula de sección para la coordenada y,
obtendremos
7k – 3 = 0
k = 3/7
Por lo tanto, el eje x divide el segmento de línea AB en la proporción de 3: 7.
Pregunta 20. Halla la razón en que el punto P(x, 2) divide el segmento de recta que une los puntos A (12, 5) y B (4, -3). Además, encuentra el valor de x.
Solución:
Suponga que P divide la línea que une A y B
y
Permita que divida el segmento en la proporción de k : 1
Después de aplicar la fórmula de sección para la coordenada y
obtendremos
2(k + 1) = -3k + 5
2k + 2 = -3k + 5
5k = 3
k = 3/5
Por lo tanto,
El segmento de recta AB se divide por P en la razón de 3 : 5
Aplicando el valor de k,
Obtendremos la coordenada x como
x = 12 + 60/8 = 72/8 = 9
Por lo tanto, las coordenadas del punto P son (9, 2).
Publicación traducida automáticamente
Artículo escrito por yashchuahan y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
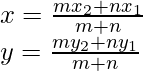




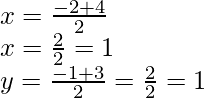
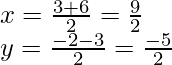
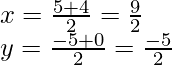
![Rendered by QuickLaTeX.com \left[\frac{3k+(-2)\times1}{k+1},\ \frac{7k+2\times1}{k+1}\right]\\ =\left[\frac{3k-2}{k+1},\ \frac{7k+2}{k+1}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2d525117daf62d2129e9497387bcc42f_l3.png)