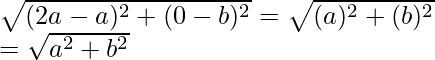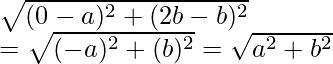Pregunta 1. Encuentra el baricentro del triángulo cuyos vértices son:
(i) (1, 4), (-1, -1) y (3, -2)
Solución:
Dados, los vértices del triángulo son (1, 4), (-1, -1) y (3, -2)
Como sabemos que las coordenadas del baricentro de un triángulo cuyos vértices son (x 1 , y 1 ), (x 2 , y 2 ), (x 3 , y 3 )
Entonces, las coordenadas del baricentro de un triángulo son
= (1, 1/3)
Por lo tanto, el baricentro del triángulo cuyos vértices son (1, 4), (-1, -1) y (3, -2) es (1, 1/3).
(i) (-2, 3), (2, -1) y (4, 0)
Solución:
Dados, los vértices del triángulo son (-2, 3), (2, -1) y (4, 0)
Como sabemos que las coordenadas del baricentro de un triángulo cuyos vértices son (x 1 , y 1 ), (x 2 , y 2 ), (x 3 , y 3 )
Entonces, las coordenadas del baricentro de un triángulo son
= (4/3, 2/3)
Por lo tanto, el baricentro del triángulo cuyos vértices son (-2, 3), (2, -1) y (4, 0) es (4/3, 2/3).
Pregunta 2. Dos vértices de un triángulo son (1, 2), (3, 5), y su baricentro está en el origen. Encuentra las coordenadas del tercer vértice.
Solución:
segun pregunta
Dos vértices de un triángulo son (1, 2), (3, 5), y su baricentro está en el origen
Encuentra: las coordenadas del tercer vértice
Entonces, supongamos que las coordenadas del tercer vértice son (x, y),
Entonces, las coordenadas del baricentro de un triángulo son
Como sabemos que el centroide está en el origen. Asi que,
(x + 1 + 3)/3 = 0
X + 4 = 0
X = -4
(y + 2 + 5)/3 = 0
y + 7 = 0
y = -7
Por lo tanto, la tercera coordenada es (-4, -7)
Pregunta 3. Encuentra el tercer vértice de un triángulo, si dos de sus vértices están en (−3, 1) y (0, −2) y el centroide está en el origen.
Solución:
Según la pregunta
ABC es un triángulo en el que las coordenadas de A son (−3, 1), B son (0, −2) y C son (a, b)
y el baricentro del triángulo ABC es (0, 0)
asi que,
(-3 + 0 + a)/3 = 0
un = 3
(1 – 2 + b)/3 = 0
segundo = 1
Por lo tanto, las coordenadas del tercer vértice son (3, 1)
Pregunta 4. A (3, 2) y B (−2, 1) son dos vértices de un triángulo ABC cuyo baricentro G tiene las coordenadas (5/3, -1/3). Encuentra las coordenadas del tercer vértice C del triángulo.
Solución:
Según la pregunta
ABC es un triángulo en el que las coordenadas de A son (3, 2), B son (−2, 1) y C son (a, b)
y el baricentro del triángulo ABC es (5/3, -1/3)
asi que,
(3 – 2 + a)/3 = 5/3
un = 4
(1 + 2 + b)/3 = -1/3
b = -4
Por lo tanto, las coordenadas del tercer vértice son (4, -4)
Pregunta 5. Si (−2, 3), (4, −3) y (4, 5) son los puntos medios de los lados de un triángulo, encuentra las coordenadas de su centroide.
Solución:

Supongamos que ABC es un triangulo
Ahora en este triángulo P, Q, R ser el punto medio del lado, AC, AB, BC.
Las coordenadas de P(−2, 3), Q (4, −3) y R(4, 5)
Supongamos que las coordenadas de A, B y C son (x1, y1), (x2, y2) y (x3, y3)
Como sabemos que P es el punto medio del lado AC,
Asi que,
(x1 + x3) /2 = -2
= x1 + x3 = -4 …..(1)
(y1 + y3) /2 = 3
= y1 + y3 = 6 …..(2)
Como sabemos que Q es el punto medio del lado AB,
Asi que,
(x1 + x2) /2 = 4
= x1 + x2 = 8 …..(3)
(y1 + y2) /2 = -3
= y1 + y2 = -6 …..(4)
Como sabemos que R es el punto medio del lado BC,
Asi que,
(x2 + x3) /2 = 4
= x2 + x3 = 8 …..(5)
(y2 + y3) /2 = 5
= y2 + y3 = 10 …..(6)
Ahora agrega c
2(x1 + x2 + x3) = -4 + 8 + 8 = 12 …..( 7)
x1 + x2 + x3 = 6
Ahora restamos eq(1), (3), (5) de eq(7), obtenemos
x1 = 10
x2 = -2
x3 = -2
De manera similar, sumando (2), (4) y (6), obtenemos
2(y1 + y2 + y3) = -6 + 6 + 10 = 10
y1 + y2 + y3 = 5 ……(8)
Ahora restamos eq(2), (4), (6) de eq(8), obtenemos
y1 = -1
y2 = 11
y3 = -5
entonces, las coordenadas del triángulo ABC son (10, -1), (-2, 11) y (-2, -5)
Por lo tanto, el baricentro del triángulo es ((10 – 2 – 2)/3, (-1 + 11 – 5)/3) = (2, 5/3)
Pregunta 6. Demostrar analíticamente que los puntos medios de dos lados de un triángulo son iguales a la mitad del tercer lado.
Solución:

En el triángulo ABC,
D y E son los puntos medios de los lados AB y AC
El DE = 1/2 aC
Sean las coordenadas de los vértices de un ∆ABC (x 1 , y 2 ), B(x 2 , y 2 ) y C(x 3 , y 3 )
Entonces las coordenadas de D serán
y las coordenadas de E serán
Longitud de BC=
……(1)
y la longitud de DE
= 1/2 aC
Por lo tanto probado
Pregunta 7. Demostrar que las líneas que unen los puntos medios de los lados opuestos de un cuadrilátero y la unión de los puntos de sus diagonales se encuentran en un punto y bisecan a otro.
Solución:

Supongamos que los vértices del cuadrilátero ABCD son A (x 1 , y 1 ), B (x 2 , y 2 ), C (x 3 , y 3 ) y D (x 4 , y 4 )
En este cuadrilátero, E y F son los puntos medios de los lados BC y AD
y EF se une a G y H son los puntos medios de la diagonal AC y BD.
GH se unen
Ahora las coordenadas de E serán
y las coordenadas de F serán
Las coordenadas de G serán
Las coordenadas de H serán
Aquí, EF y GH se cruzan en M.
Entonces, sea M el punto medio de EF, entonces sus coordenadas serán
Sea M el punto medio de GH, entonces sus coordenadas de M serán
Aquí, concluimos que las coordenadas de en ambos casos son las mismas
Por lo tanto, EF y GH se bisecan en M
Pregunta 8. Si G es el baricentro de un triángulo ABC y P es cualquier otro punto del plano, demuestre que PA 2 + PB 2 + PC 2 = GA 2 + GB 2 + GC 2 + 3GP.
Solución:

Según la pregunta
ABC es un triángulo, G es el baricentro del mismo, sea P(h, x) cualquier punto del plano.
Tenemos que probar que PA 2 + PB 2 + PC 2 = GA 2 + GB 2 + GC 2 + 3GP
Prueba:
En el triángulo ABC,
Supongamos que las coordenadas de son(x 1 , y 1 ) de B son(x 2 , y 2 ), y de C son(x 3 , y 3 )
Por lo tanto, las coordenadas del centroide G serán (u, v)
Donde u = (x 1 + x 2 + 3)/3 y v = (y 1 + y 2 + 3)/3
Ahora, encontraremos LHS y RHS por separado.
PA 2 + PB 2 + PC 2 = (h – x 1 ) 2 + (k – y 1 ) 2 + (h – x 2 ) 2 + (k – y 2 ) 2 + (h – x 3 ) 2 + ( k – y 3 ) 2
Por lo tanto probado
Pregunta 9. Si G es el baricentro del triángulo ABC, demuestre que AB 2 + BC 2 + CA 2 = 3(GA 2 + GB 2 + GC 2 ).
Solución:

Según la pregunta
ABC es un triángulo y G es el baricentro de este triángulo
Tenemos que probar que AB 2 + BC 2 + CA 2 = 3(GA 2 + GB 2 + GC 2 )
Prueba:
Supongamos que las coordenadas de los vértices de ∆ABC son
A(x 1 , y 1 ), B(x 2 , y 2 ) y C(x 3 , y 3 ) y sea G el baricentro del triángulo
Por lo tanto, las coordenadas de G serán
Ahora LHS= AB 2 + BC 2 + CA 2
= (x 1 – x 2 ) 2 + (y 1 – y 2 ) 2 + (x 2 – x 3 ) 2 + (y 2 – y 3 ) 2 + (x 3 – x 1 ) 2 + (y 3 – y 1 ) 2
RHS = 3[GA 2 + GB 2 + GC 2 ]
= LHS
Por lo tanto probado
Pregunta 10. En la figura, se da un triángulo rectángulo BOA. C es el punto medio de la hipotenusa AB. Demuestre que es equidistante de los vértices O, A y B.

Solución:
En el triángulo rectángulo OAB,
Las coordenadas de O son (0, 0), A son (2a, 0) y de B son (0, 2b)
C es el punto medio de AB. Entonces, las coordenadas de C serán
o
Ahora CO =
AC =
CC =
Entonces, podemos concluir que, CO = CA = CB
Por tanto, C es equidistante para formar los vértices O, A y B.
Por lo tanto probado
Publicación traducida automáticamente
Artículo escrito por ysachin2314 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
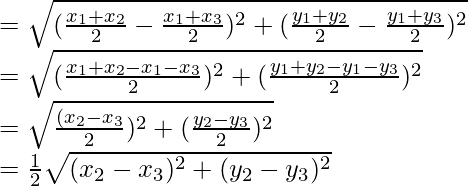
![Rendered by QuickLaTeX.com =3(h^2+k^2)+(x^2_1+x^2_2+x_3^2)+(y_1^2+y^2_2+y_3^2)-2h(x_1+x_2+x_3)-2k(y_1+y_2+y_3)\\ =3(h^2+k^2)+(x_1^2+x_2^2+x_3^2)+(y_1^2+y_2^2+y_3^2)-2h(3u)-2k(3v)\\ =3(h^2+k^2)-6hu-6kv+(x_1^2+x_2^2+x_3^2)+(x_1^2+x_2^2+x_3^2)GA^2+GB^2+GC^2+3GD^2\\ =(u-x_1)^2+(v-y_1)^2+(u-x_2)^2+(v-y_2)^2+(u-x_3)^2+(v-y_3)^2+3[(u-h)^2+(v-k)^2]\\](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a506ae766ea9fb67f9fa2661db35f91e_l3.png)
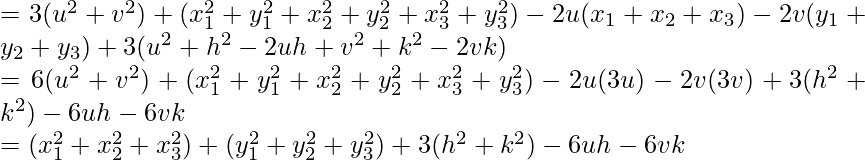
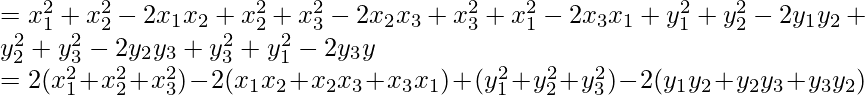
![Rendered by QuickLaTeX.com =3[(x_1-\frac{x_1+x_2+x_3}{3})^2+(y_1-\frac{y_1+y_2+y_3}{3})^2+(x_2-\frac{x_1+x_2+x_3}{3})^2+(y2-\frac{y_1+y_2+y_3}{3})^2+(x_3-\frac{x_1+x_2+x_3}{3})^3+(y_3-\frac{y_1+y_2+y_3}{3})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0e56ac02a7f9617a2d11b837d2f289ac_l3.png)
![Rendered by QuickLaTeX.com =3[\frac{(2x_1-x_2-x_3}{3})^2+(\frac{2y_1+y_2-y_3}{3})^2+(\frac{2x_2-x_1-x_3}{3})^2+(\frac{2y_2-y_1-y_3}{3})^2+(\frac{2y_3-x_1-x_2}{3})^2+(\frac{2y_3-y_2-y_3}{3})^2]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1add7f91c8bf3975b46effe745e53b8e_l3.png)
![Rendered by QuickLaTeX.com =\frac{1}{3}[6x_1^2+6x_2^2-6x_1^2-6x_1x_2-6x_2x_3-6x_3x_1+6y_1^2+6y_2^2+6y_3^2-6y_1y_2-6y_2y_3-6y_3y_1]\\ =2[(x_1^2+x_2^2+x_3^2)-2(x_1x_2+x_2x_3+x_3x_1)+2(y_1^2+y_2^2+y_3^2+y_3^2+y_3^2)-2(y_1y_2+y_2y_3+y_3y_1)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4aa5d894610c1d5c82be558d717007a4_l3.png)