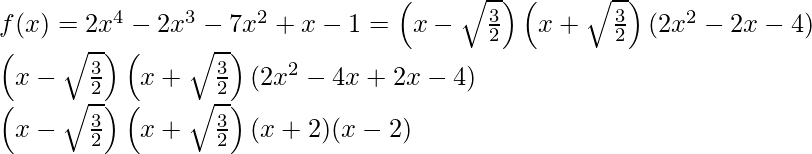Clase 10 Soluciones RD Sharma – Capítulo 2 Polinomios – Ejercicio 2.3

Pregunta 1. Aplicar el algoritmo de división para encontrar el cociente q(x) y el resto r(x) al dividir f(x) por g(x) en cada uno de los siguientes:

(i) f(x) = x ³ – 6x ² + 11x – 6, g(x) = x ² + x + 1

(ii) f(x) = 10x ⁴ + 17x ³ – 62x ² + 30x – 105, g(x) = 2x ² + 7x + 1

(iii) f(x) = 4x ³ + 8x ² + 8x + 7, g(x) = 2x ² – x + 1

(iv) f(x) = 15x ³ – 20x ² + 13x – 12, g(x) = x ² – 2x + 2

Solución:

(i) Aquí tenemos que dividir f(x) = x ³ – 6x ² + 11x – 6 por g(x) = x ² + x + 1

Entonces, para obtener el cociente q(x) y el resto r(x), usamos el algoritmo de división

Por lo tanto,

Resto r(x) = 17x – 1

Cociente q(x) = x – 7

(ii) Aquí tenemos que dividir f(x) = 10x ⁴ + 17x ³ – 62x ² + 30x – 105 por g(x) = 2x ² + 7x + 1

Entonces, para obtener el cociente q(x) y el resto r(x), usamos el algoritmo de división

Por lo tanto,

Resto r(x) = 53x – 1

Cociente q(x) = 5x ² – 9x – 2

(iii) Aquí tenemos que dividir f(x) = 4x ³ + 8x ² + 8x + 7 por g(x) =2x ² – x + 1

Entonces, para obtener el cociente q(x) y el resto r(x), usamos el algoritmo de división

Por lo tanto,

Resto r(x) = 11x + 2

Cociente q(x) = 2x – 5

(iv) f(x) = 15x ³ – 20x ² + 13x – 12, g(x) = x ² – 2x + 2

Aquí tenemos que dividir f(x) = 15x ³ – 20x ² + 13x – 12 por g(x) = x ² – 2x + 2

Entonces, para obtener el cociente q(x) y el resto r(x), usamos el algoritmo de división

Por lo tanto,

Resto r(x) = 3x + 32

Cociente q(x) = 15x + 10

Pregunta 2. Comprueba si el primer polinomio es un factor del segundo polinomio aplicando el algoritmo de división:

(i) g(t) = t ² – 3; f(t) = 2t ⁴ + 3t ³ – 2t ² – 9t – 12

(ii) g(x) = x2 ^– 3x + 1; f(x) = x ⁵ – 4x ³ + x ² + 3x + 1

(iii) g(x) = 2x ² – x + 3; f(x) = 6x ⁵ − x ⁴ + 4x ³ – 5x ² – x – 15

Solución:

(i) Aquí, tenemos que comprobar si g(t) = t ² – 3 es un factor de f(t) = 2t ⁴ + 3t ³ – 2t ² – 9t – 12

Entonces, usando el algoritmo de división, obtenemos

Como el resto que queda es 0.

Por lo tanto,

g(t) = t ² – 3 es un factor de f(t) = 2t ⁴ + 3t ³ – 2t ² – 9t – 12

(ii) Aquí, tenemos que comprobar si g(x) = x ² – 3x + 1 es un factor de(x) = x ⁵ – 4x ³ + x ² + 3x + 1

Entonces, usando el algoritmo de división, obtenemos

Como el resto que queda es 2.

Por lo tanto,

g(x) = x ² – 3x + 1 no es factor de f(x) = x ⁵ – 4x ³ + x ² + 3x + 1

(iii) Aquí, tenemos que comprobar si g(x) = 2x ² – x + 3 es un factor de f(x) = 6x ⁵ − x ⁴ + 4x ³ – 5x ² – x – 15

Entonces, usando el algoritmo de división, obtenemos

Como el resto que queda es 0.

Por lo tanto,

g(x) = 2x ² – x + 3 es un factor de f(x) = 6x ⁵ − x ⁴ + 4x ³ – 5x ² – x – 15

Pregunta 3. Obtener todos los ceros del polinomio f(x) = f(x) = 2x ⁴ + x ³ – 14x ² – 19x – 6, si dos de sus ceros son -2 y -1.

Solución:

Dado: f(x) = 2x ⁴ + x ³ – 14x ² – 19x – 6

Aquí hemos dado los dos ceros del polinomio que son -2 y -1,

Por lo tanto, sus factores serán (x + 2) y (x + 1)

Más lejos,

(x + 2)(x + 1) = x ² + x + 2x + 2 = x ² + 3x + 2

Entonces, usando el algoritmo de división, obtenemos

f(x) = 2x ⁴ + x ³ – 14x ² – 19x – 6 = (2x ² – 5x – 3)(x ² + 3x + 2)

= (2x + 1)(x – 3)(x + 2)(x + 1)

Por lo tanto, los factores de f(x) = 2x ⁴ + x ³ – 14x ² – 19x – 6 son (2x + 1), (x – 3), (x + 2), (x + 1)

Por lo tanto, los ceros del polinomio son -1/2, 3, -2, -1

Pregunta 4. Obtener todos los ceros de f(x) = x ³ + 13x ² + 32x + 20, si uno de sus ceros es -2.

Solución:

Nos han dado que el cero del polinomio f(x) = x ³ + 13x ² + 32x + 20 es -2.

Por lo tanto, su factor es (x + 2).

Entonces, usando el algoritmo de división, obtenemos

De este modo,

f(x) = x3 ⁺ 13×2 ⁺ 32x + 20

= (x2 + 11x + 10)(x + 2 ⁾

= (x2 + 10x + x + 10)(x + 2 ⁾

= (x + 10)(x + 1)(x + 2)

Por lo tanto, los factores de f(x) = x ³ + 13x ² + 32x + 20 son (x + 10), (x + 1), (x + 2)

Así, los ceros del polinomio son -1, -10, -2.

Pregunta 5. Obtener todos los ceros del polinomio f(x) = x ⁴ – 3x ³ – x ² + 9x – 6, si sus dos ceros son -√3 y √3.

Solución:

Aquí, tenemos dos ceros del polinomio f(x) = x ⁴ – 3x ³ – x ² + 9x – 6 que son -√3 y √3.

Por lo tanto, los factores son (x + √3)(x − √3) ⇒ x ² – 3.

Entonces, usando el algoritmo de división, obtenemos

Por eso,

f(x) = x ⁴ – 3x ² – x ² + 9x – 6 = (x ² – 3)(x ² – 3x + 2)

(x + √3)(x – √3)(x ² – 2x – 2 + 2)

= (x + √3)(x – √3)(x – 1)(x – 2)

Por lo tanto, los factores de f(x) = x ⁴ – 3x ³ – x ² + 9x – 6 son (x + √3)(x – √3)(x – 1)(x – 2).

Por tanto, los ceros del polinomio son -√3, √3, 1, 2.

Pregunta 6. Obtener todos los ceros del polinomio f(x) = 2x ⁴ – 2x ³ – 7x ² + x – 1, si sus dos ceros son -√3/2 y √3/2.

Solución:

Aquí, tenemos dos ceros del polinomio f(x) = 2x ⁴ – 2x ³ – 7x ² + x – 1 que son -√3/2 y √3/2.

Entonces, los factores son $\left(x-\sqrt\frac{3}{2}\right) \left(x+\sqrt\frac{3}{2}\right)$ ⇒ x ² – 3/2.

Entonces, usando el algoritmo de división, obtenemos

Por eso,

$f(x) = 2x^4- 2x^3-7x^2+ x - 1=\left(x-\sqrt\frac{3}{2}\right) \left(x+\sqrt\frac{3}{2}\right)(2x^2-2x-4)\\ \left(x-\sqrt\frac{3}{2}\right)\left(x+\sqrt\frac{3}{2}\right)(2x^2-4x+2x-4)\\ \left(x-\sqrt\frac{3}{2}\right)\left(x+\sqrt\frac{3}{2}\right)(x+2)(x-2)$

Los factores de f(x) = 2x ⁴ – 2x ³ – 7x ² + x – 1 son $\left(x-\sqrt\frac{3}{2}\right),\ \left(x+\sqrt\frac{3}{2}\right),\ (x+2),\ (x-2)$ .

Así, los ceros del polinomio son -1, 2, -√3/2 y √3/2.

Pregunta 7. Encuentra todos los ceros del polinomio x ⁴ + x ³ – 34x ² – 4x + 120, si sus dos ceros son 2 y – 2.

Solución:

Aquí, nos dan dos ceros del polinomio x ⁴ + x ³ – 34x ² – 4x + 120 que son 2 y -2.

Por lo tanto, los factores son (x + 2)(x – 2)⇒ x ² – 4.

Entonces, usando el algoritmo de división, obtenemos

Por eso,

x ⁴ + x ³ – 34x ² – 4x + 120 = (x ² – 4)(x ² + x – 30)

= (x – 2)(x + 2)(x ² + 6x – 5x – 30)

= (x – 2)(x + 2)(x + 6)(x – 5)

Entonces, los factores de x ⁴ + x ³ – 34x ² – 4x + 120 son (x – 2), (x + 2), (x + 6), (x – 5)

Así, los ceros del polinomio = x = 2, – 2, – 6, 5

Pregunta 8. Encuentra todos los ceros del polinomio 2x ⁴ + 7x ³ – 19x ² – 14x + 30, si sus dos ceros son √2 y -√2.

Solución:

Aquí, nos dan dos ceros del polinomio 2x ⁴ + 7x ³ – 19x ² – 14x + 30 ² que son √2 y -√2.

Por lo tanto, los factores son (x + √2)(x – √2) ⇒ x ² – 2.

Entonces, usando el algoritmo de división, obtenemos

Por eso,

2x ⁴ + 7x ³ – 19x ² – 14x + 30 = (x ² – 2)(2x ² + 7x – 15)

= (2x ² + 10x – 3x – 15)(x + √2)(x – √2)

= (2x – 3)(x + 5)(x + √2)(x – √2)

Entonces, los factores de 2x ⁴ + 7x ³ – 19x ² – 14x + 30 son (2x – 3), (x + 5), (x + √2), (x – √2)

Así, los ceros del polinomio son √2, -√2, -5, 3/2.

Pregunta 9. Encuentra todos los ceros del polinomio f(x) = 2x ³ + x ² – 6x – 3, si dos de sus ceros son -√3 y √3.

Solución:

Aquí, nos dan dos ceros del polinomio f(x) = 2x ³ + x ² – 6x – 3 que son -√3 y √3.

Por lo tanto, los factores son (x + √3)(x – √3) ⇒ x ² – 3.

Entonces, usando el algoritmo de división, obtenemos

Por eso,

f(x) = 2x ³ + x ² – 6x – 3

= (x ² – 3)(2x + 1)

= (x + √3)(x – √3)(2x + 1)

Los factores de f(x) = 2x ³ + x ² – 6x – 3 son (x + √3), (x – √3), 2x + 1

Por lo tanto, los ceros para el polinomio dado son √3, -√3, -1/2

Pregunta 10. Encuentra todos los ceros del polinomio f(x) = x ³ + 3x ² – 2x – 6, si sus dos ceros son √2 y -√2.

Solución:

Aquí, nos dan dos ceros del polinomio f(x) = x ³ + 3x ² – 2x – 6 que son √2 y -√2.

Por lo tanto, los factores son (x + √2)(x – √2)⇒ x ² – 2.

Entonces, usando el algoritmo de división, obtenemos

Por eso,

f(x) = x3 ⁺ 3×2 – ^2x – 6

= (x ² – 2) (x + 3)

= (x + √2)(x – √2)(x + 3)

Los factores de f(x) = x ³ + 3x ² – 2x – 6 son (x + √2), (x – √2), (x + 3)

Por lo tanto, los ceros del polinomio dado son -√2, √2 y – 3.

Pregunta 11. ¿Qué se debe sumar al polinomio f(x) = x ⁴ + 2x ³ – 2x ² + x − 1 para que el polinomio resultante sea exactamente divisible por g(x) = x ² + 2x − 3.

Solución:

Aquí tenemos que sumar al polinomio f(x) = x ⁴ + 2x ³ – 2x ² + x − 1 para que el

el polinomio resultante es exactamente divisible por g(x) = x ² + 2x − 3.

Entonces, divide f(x) = x ⁴ + 2x ³ – 2x ² + x − 1 entre g(x) = x ² + 2x − 3 para obtener la respuesta.

Como el resto que queda es (x – 2) para obtener el polinomio resultante exactamente divisible por

g(x) = x ² + 2x − 3 debemos sumar (x – 2) a f(x) = x ⁴ + 2x ³ – 2x ² + x − 1.

Pregunta 12. ¿Qué se debe restar del polinomio f(x) = x ⁴ + 2x ³ – 13x ² –12x + 21 para que el polinomio resultante sea exactamente divisible por g(x) = x ² – 4x + 3.

Solución:

Aquí tenemos que restar al polinomio f(x) = x ⁴ + 2x ³ – 13x ² – 12x + 21

para que el polinomio resultante sea exactamente divisible por g(x) = x ² – 4x + 3.

Entonces, divide f(x) = x ⁴ + 2x ³ – 13x ² – 12x + 21 entre g(x) = x ² – 4x + 3 para obtener la respuesta.

Como el resto que queda es (2x – 3) para obtener el polinomio resultante exactamente divisible por

g(x) = x ² – 4x + 3 debemos sumar (2x – 3) a f(x) = x ⁴ + 2x ³ – 13x ² – 12x + 21.

Pregunta 13. Dado que √2 es un cero del polinomio cúbico f(x) = 6x ³ + √2x ² – 10x – 4√2, encuentre sus otros dos ceros.

Solución:

Aquí, sabemos que √2 es el cero del polinomio cúbico

f(x) = 6x ³ + √2x ² – 10x – 4√2, por lo tanto, el factor del polinomio es (x – √2)

Entonces, usando el algoritmo de división, obtenemos

Por eso,

f(x) = 6x ³ + √2x ² – 10x – 4√2

= (x – √2)(6x ² + 7√2x + 4)

= (x – √2)(6x ² + 4√2x + 3√2x + 4)

= (x – √2)(3x + 2√2)(2x + √2)

Los factores de f(x) = 6x ³ + √2x ² – 10x – 4√2 son (x – √2), (3x + 2√2), (2x + √2)

Por lo tanto, los ceros del polinomio son -2√2/3, -√2/2, √2

Pregunta 14. Dado que x – √5 es un factor del polinomio cúbico x ³ – 3√5x ² + 13x – 3√5, encuentre todos los ceros del polinomio.

Solución:

Aquí tenemos x – √5 como factor del polinomio cúbico x ³ – 3√5x ² + 13x – 3√5

Para encontrar todos los ceros del polinomio, tenemos que dividir el polinomio x ³ – 3√5x ² + 13x – 3√5 por el factor x – √5

Por eso,

x ³ – 3√5x ² + 13x – 3√5

= (x – √5)(x2 – 2√5 + 3 ⁾

= (x – √5)(x – (√5 + √2))(x – (√5 – √2))

Entonces, los factores del polinomio cúbico x ³ – 3√5x ² + 13x – 3√5 son (x – √5), (x – (√5 + √2)), (x – (√5 – √2) ))

Por lo tanto, los ceros del polinomio son √5, (√5 – √2), (√5 + √2)

Publicación traducida automáticamente

Artículo escrito por yashchuahan y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1. Aplicar el algoritmo de división para encontrar el cociente q(x) y el resto r(x) al dividir f(x) por g(x) en cada uno de los siguientes:

Pregunta 2. Comprueba si el primer polinomio es un factor del segundo polinomio aplicando el algoritmo de división:

Pregunta 3. Obtener todos los ceros del polinomio f(x) = f(x) = 2x 4 + x 3 – 14x 2 – 19x – 6, si dos de sus ceros son -2 y -1.

Pregunta 4. Obtener todos los ceros de f(x) = x 3 + 13x 2 + 32x + 20, si uno de sus ceros es -2.

Pregunta 5. Obtener todos los ceros del polinomio f(x) = x 4 – 3x 3 – x 2 + 9x – 6, si sus dos ceros son -√3 y √3.

Pregunta 6. Obtener todos los ceros del polinomio f(x) = 2x 4 – 2x 3 – 7x 2 + x – 1, si sus dos ceros son -√3/2 y √3/2.

Pregunta 7. Encuentra todos los ceros del polinomio x 4 + x 3 – 34x 2 – 4x + 120, si sus dos ceros son 2 y – 2.

Pregunta 8. Encuentra todos los ceros del polinomio 2x 4 + 7x 3 – 19x 2 – 14x + 30, si sus dos ceros son √2 y -√2.

Pregunta 9. Encuentra todos los ceros del polinomio f(x) = 2x 3 + x 2 – 6x – 3, si dos de sus ceros son -√3 y √3.

Pregunta 10. Encuentra todos los ceros del polinomio f(x) = x 3 + 3x 2 – 2x – 6, si sus dos ceros son √2 y -√2.

Pregunta 11. ¿Qué se debe sumar al polinomio f(x) = x 4 + 2x 3 – 2x 2 + x − 1 para que el polinomio resultante sea exactamente divisible por g(x) = x 2 + 2x − 3.

Pregunta 12. ¿Qué se debe restar del polinomio f(x) = x 4 + 2x 3 – 13x 2 –12x + 21 para que el polinomio resultante sea exactamente divisible por g(x) = x 2 – 4x + 3.

Pregunta 13. Dado que √2 es un cero del polinomio cúbico f(x) = 6x 3 + √2x 2 – 10x – 4√2, encuentre sus otros dos ceros.

Pregunta 14. Dado que x – √5 es un factor del polinomio cúbico x 3 – 3√5x 2 + 13x – 3√5, encuentre todos los ceros del polinomio.

Deja una respuesta Cancelar la respuesta

Pregunta 3. Obtener todos los ceros del polinomio f(x) = f(x) = 2x ⁴ + x ³ – 14x ² – 19x – 6, si dos de sus ceros son -2 y -1.

Pregunta 4. Obtener todos los ceros de f(x) = x ³ + 13x ² + 32x + 20, si uno de sus ceros es -2.

Pregunta 5. Obtener todos los ceros del polinomio f(x) = x ⁴ – 3x ³ – x ² + 9x – 6, si sus dos ceros son -√3 y √3.

Pregunta 6. Obtener todos los ceros del polinomio f(x) = 2x ⁴ – 2x ³ – 7x ² + x – 1, si sus dos ceros son -√3/2 y √3/2.

Pregunta 7. Encuentra todos los ceros del polinomio x ⁴ + x ³ – 34x ² – 4x + 120, si sus dos ceros son 2 y – 2.

Pregunta 8. Encuentra todos los ceros del polinomio 2x ⁴ + 7x ³ – 19x ² – 14x + 30, si sus dos ceros son √2 y -√2.

Pregunta 9. Encuentra todos los ceros del polinomio f(x) = 2x ³ + x ² – 6x – 3, si dos de sus ceros son -√3 y √3.

Pregunta 10. Encuentra todos los ceros del polinomio f(x) = x ³ + 3x ² – 2x – 6, si sus dos ceros son √2 y -√2.

Pregunta 11. ¿Qué se debe sumar al polinomio f(x) = x ⁴ + 2x ³ – 2x ² + x − 1 para que el polinomio resultante sea exactamente divisible por g(x) = x ² + 2x − 3.

Pregunta 12. ¿Qué se debe restar del polinomio f(x) = x ⁴ + 2x ³ – 13x ² –12x + 21 para que el polinomio resultante sea exactamente divisible por g(x) = x ² – 4x + 3.

Pregunta 13. Dado que √2 es un cero del polinomio cúbico f(x) = 6x ³ + √2x ² – 10x – 4√2, encuentre sus otros dos ceros.

Pregunta 14. Dado que x – √5 es un factor del polinomio cúbico x ³ – 3√5x ² + 13x – 3√5, encuentre todos los ceros del polinomio.