Pregunta 1. Resuelva gráficamente la siguiente ecuación
x + y = 3
2x + 5y = 12
Solución:
Dado que, 2x + 5y = 12 y x + y = 3
Tenemos,
x + y = 3,
Cuando y = 0, obtenemos x = 3
Cuando x = 0, obtenemos y = 3
Entonces, la siguiente tabla da puntos en la línea x + y = 3:
X 0 3 y 3 0 Ahora, 2 + 5y = 12
y = (12 – 2x)/5
Cuando x = 1, tenemos
y = (12 – 2)/5 = 4
Cuando x = -4, tenemos
y = (12 – 2(-4))/5 = 4
Entonces, la siguiente tabla da puntos en la línea 2x + 5y = 12:
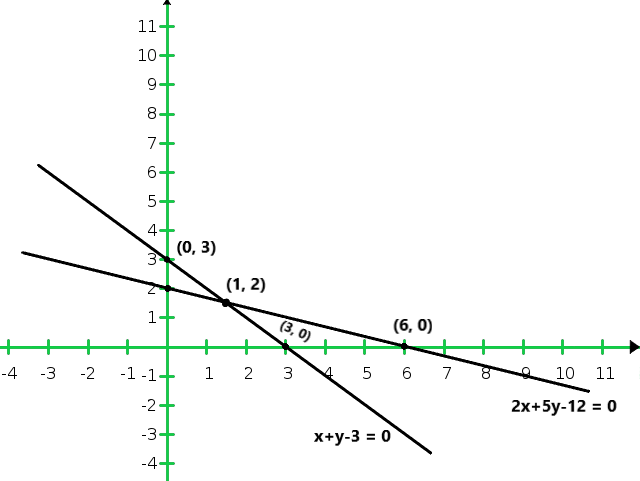
X 1 -4 y 2 4 Entonces, la gráfica de la ecuación x + y = 3 y 2x + 5y = 12 es
Del gráfico concluimos que las dos líneas se cortan en un punto P (1, 2).
Por lo tanto, x = 1 y y = 2 son puntos requeridos.
Pregunta 2. Resuelva gráficamente la siguiente ecuación
x-2y = 5
2x + 3y = 10
Solución :
Dado que,, x – 2y = 5 y 2x + 3y = 10
Ahora, x – 2y = 5
x = 5 + 2y
Cuando y = 0, obtenemos x = 5
Cuando y = -2, obtenemos x = 1
Entonces, la siguiente tabla da puntos en la línea x – 2y = 5
X 5 -1 y 0 -2 Ahora, 2x + 3y = 10
x = (10 – 3 años)/2
Cuando y = 0, obtenemos x = 5
Cuando y = 2, obtenemos x = 2
Entonces, la siguiente tabla da puntos en la línea 2x + 3y = 10
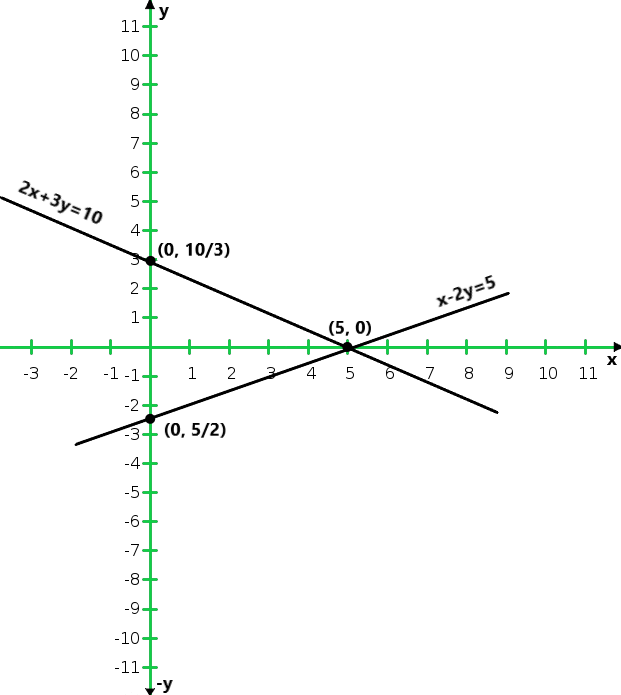
X 5 2 y 0 2 Entonces, la gráfica de la ecuación x – 2y = 5 y 2x + 3y = 10
Del gráfico concluimos que las dos líneas se cortan en un punto P (5, 0)
Por lo tanto, x = 5 y y = 0 son puntos requeridos.
Pregunta 3. Resuelva gráficamente la siguiente ecuación
3x + y + 1 = 0
2x – 3y + 8 = 0
Solución:
Dado que, 3x + y + 1 = 0 y 2x – 3y + 8 = 0
Ahora 3x + y + 1 = 0
y = -1 – 3x
Cuando x = 0, obtenemos x = -1
Cuando y = -1, obtenemos x = 2
Entonces, la siguiente tabla da puntos en la línea x – 2y = 5
X -1 0 y 2 -1 Ahora, 2x – 3y + 8 = 0
x = (3y – 8)/2
Cuando y = 0, obtenemos x = -4
Cuando y = 2, obtenemos x = 1
Entonces, la siguiente tabla da puntos en la línea 2x + 3y = 10
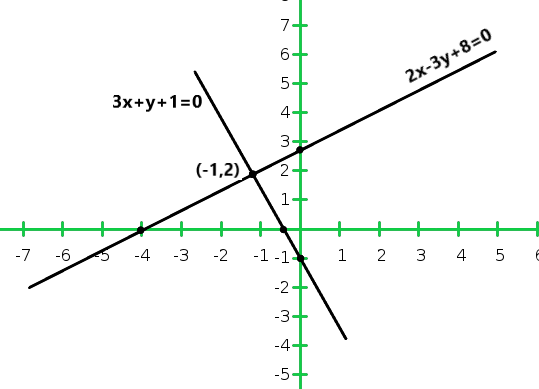
X -4 -1 y 0 -2 Entonces, la gráfica de la ecuación 3x + y + 1 = 0 y 2x – 3y + 8 = 0
Del gráfico concluimos que las dos líneas se cortan en un punto P (-1, 2)
Por lo tanto, x = -1 e y = 2 son puntos requeridos.
Pregunta 4. Resuelva gráficamente la siguiente ecuación
2x + y – 3 = 0
2x – 3y – 7 = 0
Solución:
Dado que,, 2x + y – 3 = 0 y 2x – 3y – 7 = 0
Ahora 2x + y – 3 = 0,
y = 3 – 2x
Cuando x = 0, obtenemos x = 3
Cuando x = 1, obtenemos x = 1
Entonces, la siguiente tabla da puntos en la línea 2x + y – 3 = 0
X 0 1 y 3 1 Ahora, 2x – 3y – 7 = 0
Cuando x = 0, obtenemos y = 1
Cuando x = 2, obtenemos y = -1
Entonces, la siguiente tabla da puntos en la línea 2x + 3y = 10
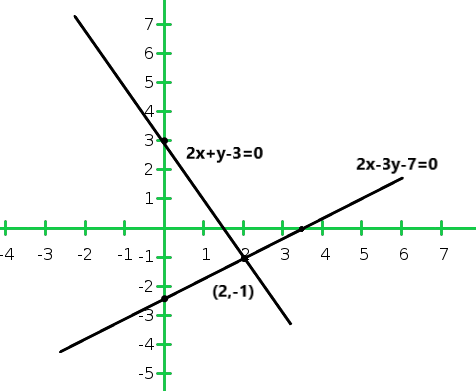
X 2 5 y -1 1 Entonces, la gráfica de la ecuación 2x + y – 3 = 0 y 2x – 3y – 7 = 0
Del gráfico concluimos que las dos rectas se cortan en un punto P (2,-1)
Por lo tanto, x = 2 y y = -1 son puntos requeridos.
Pregunta 5. Resuelva gráficamente la siguiente ecuación
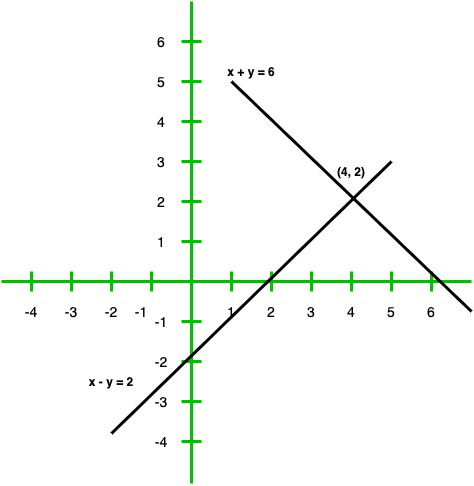
x + y = 6
x – y = 2
Solución:
Dado que, x + y = 6 y x – y = 2
Ahora x + y = 6
y = 6 – x
Cuando x = 2, obtenemos y = 4
Cuando x = 3, obtenemos y = 3
Entonces, la siguiente tabla da puntos en la línea x + y = 6
X 2 3 y 4 3 Ahora, x – y = 2
y = x – 2
Cuando x = 0, obtenemos y = – 2
Cuando x = 2, obtenemos y = 0
Entonces, la siguiente tabla da puntos en la línea x – y = 2
X 0 2 y -2 0 Entonces, la gráfica de la ecuación x + y = 6 y x – y = 2
Del gráfico concluimos que las dos líneas se cortan en un punto P (4, 2)
Por lo tanto, x = 4 e y = 2 son puntos requeridos.
Pregunta 6. Resuelva gráficamente la siguiente ecuación
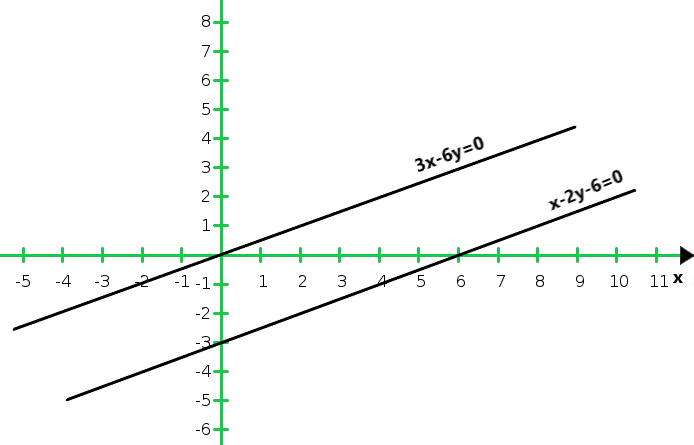
x-2y = 6
3x – 6y = 0
Solución:
Dado que, x – 2y = 6 y 3x – 6y = 0
Ahora x – 2y = 6
x = 6 + 2y
Cuando y = -2, obtenemos x = 2
Cuando y = -3, obtenemos x = 0
Entonces, la siguiente tabla da puntos en la línea x – 2y = 6
X 2 0 y -2 -3 Ahora, 3x – 6y = 0
= x = 2y
Cuando y = 0, obtenemos y = 0
Cuando y = -1, obtenemos x = 2
Entonces, la siguiente tabla da puntos en la línea 3x – 6y = 0
X 0 2 y 0 1 Entonces, la gráfica de la ecuación x – 2y = 6 y 3x – 6y = 0
Del gráfico concluimos que las dos líneas son paralelas entre sí, por lo que las dos líneas no tienen un punto común.
Por lo tanto, el sistema dado no tiene soluciones.
Pregunta 7. Resuelva gráficamente la siguiente ecuación
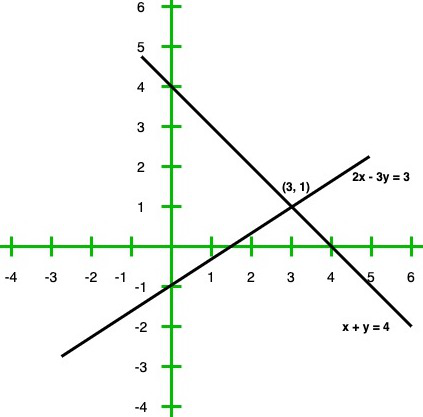
x + y = 4
2x – 3y = 3
Solución:
Dado que, x + y = 4 y 2x – 3y = 3
Ahora x + y = 4
x = 4 – y
Cuando y = 0, obtenemos x = 4
Cuando y = 2, obtenemos x = 2
Entonces, la siguiente tabla da puntos en la línea x + y = 4
X 4 2 y 0 2 Ahora, 2x – 3y = 3
x = (3y + 3)/2
Cuando y = 1, obtenemos x = 3
Cuando y = -1, obtenemos x = 0
Entonces, la siguiente tabla da puntos en la línea 2x – 3y = 3
X 3 0 y 1 -1 Entonces, la gráfica de la ecuación x + y = 4 y 2x – 3y = 3
Del gráfico concluimos que las dos rectas se cortan en un punto P(3, 1)
Por lo tanto, x = 3 e y = 1 son puntos requeridos.
Pregunta 8. Resuelva gráficamente la siguiente ecuación
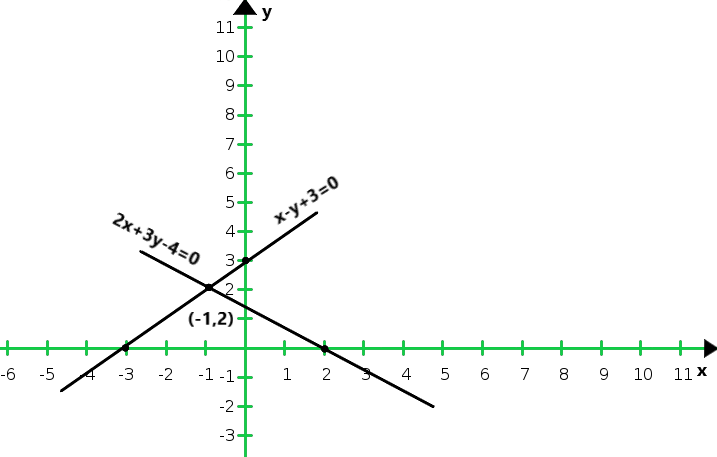
2x + 3y = 4
x – y + 3 = 0
Solución:
Dado que, 2x + 3y = 4 y x – y + 3 = 0
Ahora 2x + 3y = 4
x = (4 – 3y)/2
Cuando y = 0, obtenemos x = 2
Cuando y = 2, obtenemos x = – 1
Entonces, la siguiente tabla da puntos en la línea x + y = 4
X -1 2 y 2 0 Ahora, x – y + 3 = 0
x = y – 3
Cuando y = 3, obtenemos x = 0
Cuando y = 4, obtenemos x = 1
Entonces, la siguiente tabla da puntos en la línea x – y + 3 = 0
X 0 1 y 3 4 Entonces, la gráfica de la ecuación 2x + 3y = 4 y x – y + 3 = 0
Del gráfico concluimos que las dos rectas se cortan en (-1, 2)
Por lo tanto, x = -1 e y = 2 son puntos requeridos.
Pregunta 9. Resuelva gráficamente la siguiente ecuación
2x – 3y + 13 = 0
3x – 2y + 12 = 0
Solución:
Dado que, 2x – 3y + 13 = 0 y 3x – 2y + 12 = 0
Ahora, 2x – 3y + 13 = 0
x = (3y – 13)/2
Cuando y = 1, obtenemos x = – 5
Cuando y = 3, obtenemos x = – 2
Entonces, la siguiente tabla da puntos en la línea 2x – 3y + 13 = 0
X -5 -2 y 1 3 Ahora, 3x – 2y + 12 = 0
x = (2y – 12)/3
Cuando y = 0, obtenemos x = -14
Cuando y = 3, obtenemos x = -2
Entonces, la siguiente tabla da puntos en la línea x – y + 3 = 0
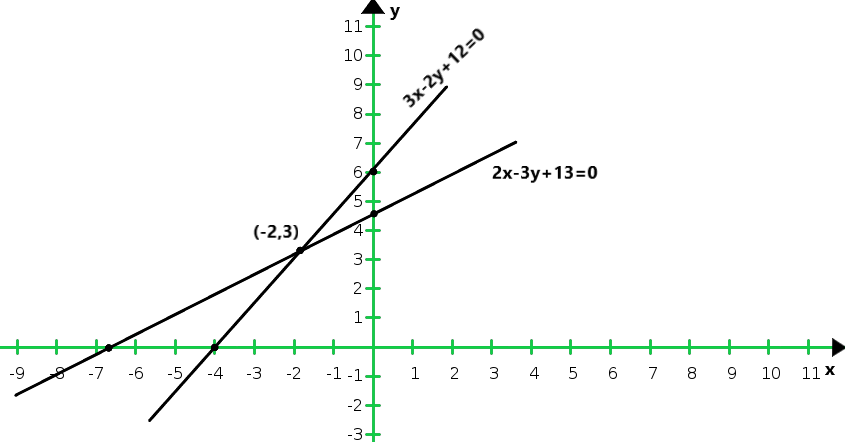
X -4 -2 y 0 3 Entonces, la gráfica de la ecuación 2x – 3y + 14 = 0 y 3x – 2y + 12 = 0
Del gráfico concluimos que las dos rectas se cortan en (- 2, 3)
Por lo tanto x = – 2 y y = 3 son puntos requeridos.
Pregunta: 10. Resuelva gráficamente la siguiente ecuación
2x + 3y + 5 = 0
3x – 2y – 12 = 0
Solución:
Dado que, 2x + 3y + 5 = 0 y 3x – 2y – 12 = 0
Ahora, 2x + 3y + 5 = 0,
x = (-3y – 5)/2
Cuando y = 1, obtenemos x = – 4
Cuando y = -1, obtenemos x = -1
Entonces, la siguiente tabla da puntos en la línea 2x + 3y + 5 = 0
X -4 -1 y 1 -1 Ahora, 3x – 2y – 12 = 0,
x = (2y + 12)/3
Cuando y = 0, obtenemos x = 4
Cuando y = 3, obtenemos x = 6
Entonces, la siguiente tabla da puntos en la línea 3x – 2y – 12 = 0
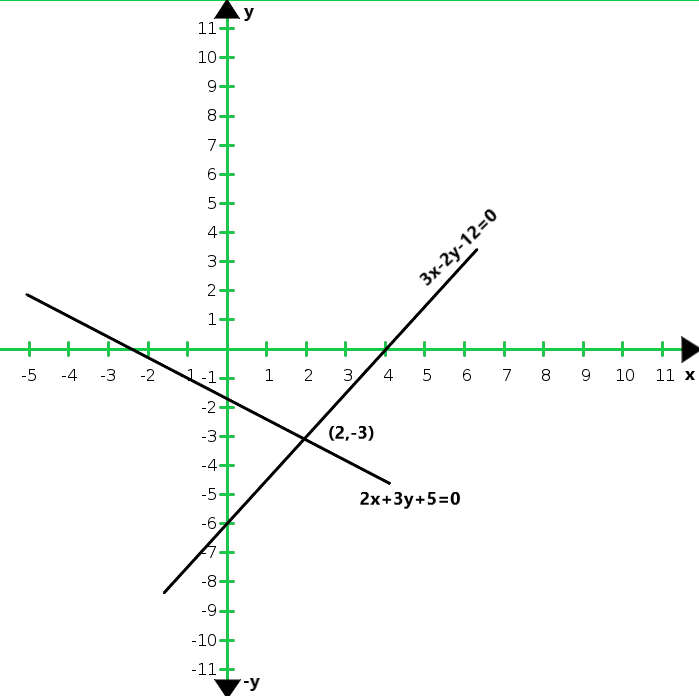
X 4 6 y 0 3 Entonces, la gráfica de la ecuación 2x + 3y + 5 = 0 y 3x – 2y – 12 = 0
Del gráfico concluimos que las dos rectas se intersecan en (2, 3).
Por lo tanto x = 2 y y = 3 son puntos requeridos.
Pregunta 11. Resuelva gráficamente la siguiente ecuación
2x + 3y = 6
4x + 6y = 12
Solución:
Dado que, 2x + 3y = 6 y 4x + 6y = 12
Ahora, 2x + 3y = 5
x = (6-3 años)/2
Cuando y = 0, obtenemos x = 3
Cuando y = 2, obtenemos x = 0
Entonces, la siguiente tabla da puntos en la línea 2x + 3y = 6
X 0 3 y 2 0 Ahora, 4x + 6y = 12
x = (12 – 6 años)/4
Cuando y = 0, obtenemos x = 3
Cuando y = 2, obtenemos x = 0
Entonces, la siguiente tabla da puntos en la línea 4x + 6y = 12
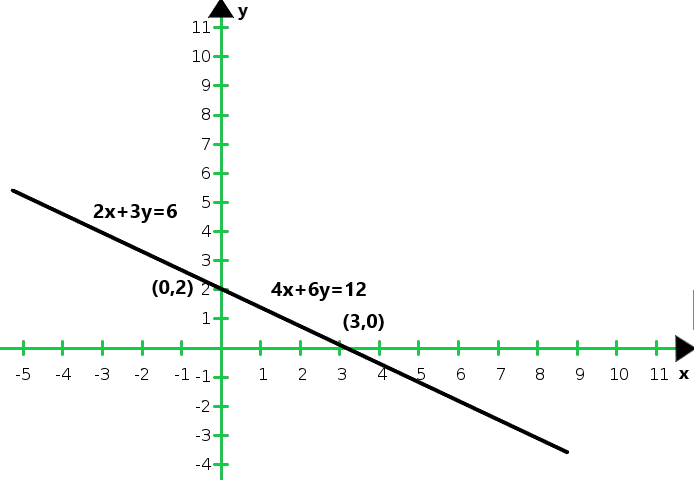
X 0 3 y 2 0 Entonces, la gráfica de la ecuación 2x + 3y = 6 y 4x + 6y = 12
Del gráfico concluimos que las dos ecuaciones son coincidentes.
Por lo tanto, el sistema de ecuaciones tiene infinitas soluciones.
Pregunta 12. Resuelva gráficamente la siguiente ecuación
x-2y = 5
3x – 6y = 15
Solución:
Dado que, x – 2y = 5 y 3x – 6y = 15
Ahora, x – 2y = 5
x = 2y + 5
Cuando y = -1, obtenemos x = 3
Cuando y = 0, obtenemos x = 5
Entonces, la siguiente tabla da puntos en la línea x – 2y = 5
X 3 5 y 1 0 Ahora, 3x – 6y = 15
x = (15 + 6y)/3
Cuando y = -2, obtenemos x = 1
Cuando y = -3, obtenemos x = -1
Entonces, la siguiente tabla da puntos en la línea 3x – 6y = 15
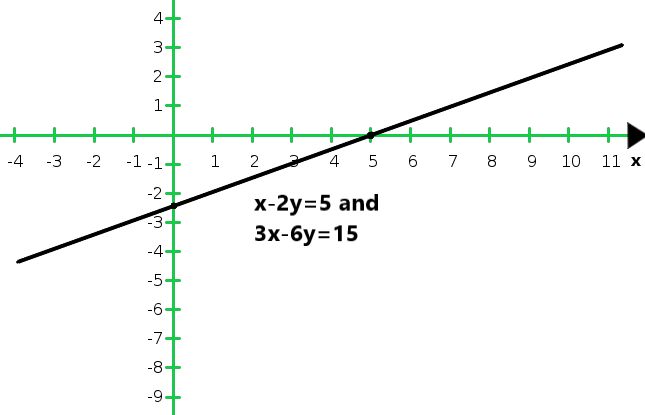
X 1 -1 y -2 -3 Entonces, la gráfica de las ecuaciones x – 2y = 5 y 3x – 6y = 15:
Del gráfico concluimos que las dos ecuaciones son coincidentes.
Por lo tanto, el sistema de ecuaciones tiene infinitas soluciones.
Pregunta 13. Resuelva gráficamente la siguiente ecuación
3x + y = 8
6x + 2y = 16
Solución:
Dado que, 3x + y = 8 y 6x + 2y = 16
Ahora, x – 2y = 5
= y = 8 – 3x
Cuando x = 2, obtenemos y = 2
Cuando x = 3, obtenemos y = -1
Entonces, la siguiente tabla da puntos en la línea 3x + y = 8
X 2 3 y 2 -1 Ahora, 6x + 2y = 16
y = (16 – 6x)/2
Cuando x = 1, obtenemos y = 5
Cuando x = 3, obtenemos y = -1
Entonces, la siguiente tabla da puntos en la línea 6x + 2y = 16
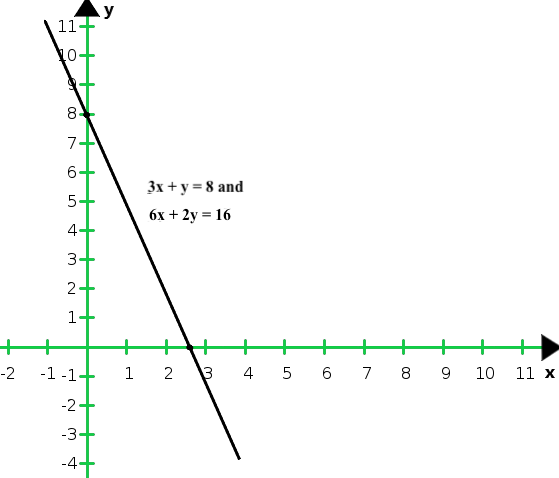
X 1 3 y 5 -1 Entonces, la gráfica de las ecuaciones dadas 3x + y = 8 y 6x + 2y = 16:
De la gráfica concluimos que las gráficas de las dos ecuaciones son coincidentes
Por lo tanto, el sistema de ecuaciones tiene infinitas soluciones.
Publicación traducida automáticamente
Artículo escrito por ronilpatil y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA