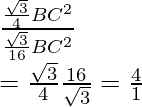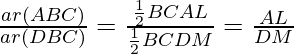Clase 10 Soluciones RD Sharma – Capítulo 4 Triángulos – Ejercicio 4.6

Pregunta 11. Las áreas de dos triángulos semejantes son 121 cm ² y 64 cm ² respectivamente. Si la mediana del primer triángulo es de 12,1 cm, encuentra la mediana correspondiente del otro.

Solución:

Consideremos ∆ABC y ∆DEF, AL y DM son las medianas de ∆ABC y ∆DEF

Se da que el área de ∆ABC = 121 cm ² y el área de ∆DEF = 64 cm ²

AL = 12,1 cm

Supongamos DM = x cm

Dado que, ∆ABC ~ ∆DEF

Asi que,

ar(∆ABC)/ar(∆DEF) = AL ² /DM ²

= 121/64 = (12.1) ² /x ²

11/8 = 12,1/x

⇒ x = (8 × 12,1)/11 = 8,8

Por lo tanto, la mediana del segundo triángulo es de 8,8 cm.

Pregunta 12. En ∆ABC ~ ∆DEF tal que AB = 5 cm y (∆ABC) = 20 cm ² y área (∆DEF) = 45 cm ² , determine DE.

Solución:

Dado que,

área (∆ABC) = 20 cm²

área (∆DEF) = 45 cm²

AB = 5cm

Consideremos DE = x cm

Además, dado que ∆ABC ~ ∆DEF

ar(∆ABC)/ar(∆DEF) = AB ² /DE ²

⇒20/45 = (5) ² /x ²

⇒20/45 = 25/ ^x2

⇒x ² = (25 × 45)/20 = 225/4 = (15/2) ²

x = 15/2 = 7,5

DE = 7,5 cm

Pregunta 13. En ∆ABC, PQ es un segmento de línea que corta a AB en P y AC en Q tal que PQ || BC y PQ dividen ∆ABC en dos partes de igual área. Encuentre BP/AB.

Solución:

Se da que, en ∆ABC, PQ || BC y la línea PQ dividen el ∆ABC en dos partes

∆APQ y trampa. BPQC por igual

es decir, área ∆APQ = área BPQC

Ahora tenemos que encontrar BP/AB.

Como sabemos que PQ||BC

Entonces, ∆APQ ∼ ∆ABC

⇒ ar.(∆APQ)/ar.(∆ABC) = AP ² /AB ²

⇒ ar.(∆ABC)/ar.(∆APQ) = AB ² /AP ²

2/1 = AB ² / AP ²

{área ∆APQ = área trampa. BPQC

Área ∆ABC = 2área (∆APQ)}

⇒AB/AP = √2/1

⇒√2 AP = AB = AP + PB

⇒√2AP – AP = PB

⇒(√2 – 1)AP = PB

PA/PA = (√2 – 1)/1

Pregunta 14. Las áreas de dos triángulos semejantes ABC y PQR están en la razón 9 : 16. Si BC = 4,5 cm, encuentra la longitud de QR.

Solución:

Dado que, área (∆ABC) : área (∆PQR) = 9 : 16

∆ABC ~ ∆PQR

y BC = 4,5 cm

Consideremos QR = x cm

Como sabemos que ∆ABC ~ ∆PQR

ar.(∆ABC)/ar.(∆PQR) = BC ² /QR ² ⇒ 9/16 = (4.5) ² /x ²

⇒ (3/4) ² = (4,5/x) ² ⇒ 4,5/x = 3/4

x = (4,5 × 4)/3 = 60

Por lo tanto, la longitud de QR es de 6 cm.

Pregunta 15. ABC es un triángulo y PQ es una recta que corta a AB en P y a AC en Q. Si AP = 1 cm, PB = 3 cm, AQ = 1,5 cm, QC = 4,5 cm, prueba que el área de ∆APQ es un dieciseisavo del área de ∆ABC.

Solución:

Dado que, en ∆ABC, P y Q son dos puntos de la recta AB y AC

AP = 1 cm, PB = 3 cm, AQ = 1,5 cm y QC = 4,5 cm

Ahora, AP/PB = 1/3 y AQ/QC = 1,5/4,5 = 1/3

En ∆APQ y ∆ABC

AP/PB = AQ/QC

PQ||BC

Por lo tanto, ∆APQ ∼ ∆ABC

Entonces, ar.(∆APQ)/ar.(∆ABC) = AP ² /PB ² = AP ² /(AP + PB) ²

ar.(∆APQ)/ar.(∆ABC) = 1 ² /(1 + 3) ² = 1/16

Por tanto, área de ∆APQ = 1/16 del área de ∆ABC

Pregunta 16. Si D es un punto del lado AB de ∆ABC tal que AD : DB = 3 : 2 y E es un punto de BC tal que DE || C.A. Encuentra la razón de las áreas de ∆ABC y ∆BDE.

Solución:

Dado que en ∆ABC, D es un punto en AB tal que AD : DB = 3 : 2

DE||CA

En ∆BDE y ∆ABC

∠BDE = ∠A

∠DBE = ∠ABC

Entonces, por AA, ∆BED ∼ ∆ABC

Por tanto, ar.(∆ABC)/ar.(∆BDE) = AB ² /BD ² = (BD + AD) ² /BD ²

= (2 + 3) 2/2 ² = 5 ^2/2² = ^25/4

Por lo tanto, la razón de áreas de ∆ABC y ∆BDE es 25:4

Pregunta 17. Si ∆ABC y ∆BDE son triángulos equiláteros, donde D es el punto medio de BC, encuentra la razón de las áreas de ∆ABC y ∆BDE.

Solución:

Dado que ∆ABC y ∆DBE son triángulos equiláteros, donde D es el punto medio de BC

Entonces, BD = 1/2BC

Ahora área de ∆ABC

√3/4(lado) ² = √3/4BC ²

y área de ∆DBE

√3/4(lado) ² = √3/4BD ²

√3/4(lado) ² = √3/4(1/2BC) ²

√3/4(lado) ² = √3/16(BC) ²

Entonces, la razón entre las áreas es

= área(∆ABC)/área(∆DBE) = $\frac{\frac{\sqrt{3}}{4}BC^2}{\frac{\sqrt{3}}{16}BC^2}\\ =\frac{\sqrt{3}}{4}×\frac{16}{\sqrt{3}}=\frac{4}{1}$

Por lo tanto, la relación de áreas de ∆ABC y ∆BDE es 4:1

Pregunta 18. Dos triángulos isósceles tienen ángulos verticales iguales y sus áreas están en la razón 36 : 25. Encuentra la razón de sus alturas correspondientes.

Solución:

Consideremos dos triángulos, ∆ABC y ∆XYZ y estos triángulos tienen el mismo ángulo vertical, es decir, ∠A y ∠X

Y AD y XO son las alturas de estos triángulos.

Entonces, ∆ABC/∆XYZ = AB/AC = XY/XZ

En ∆ABC y ∆XYZ

∠A = ∠X

AB/CA = XY/XZ

Entonces, por SAS

∆ABC ~ ∆XYZ

Entonces, ar(∆ABC)/ar(∆XYZ) = AD ² /XO ²

Como sabemos que ar(∆ABC)/ar(∆XYZ) = 36/25

Asi que,

36/25 = ² d.C./XO ²

6/5 = DA/XO

Por lo tanto, la razón de sus alturas correspondientes es 6:5

Pregunta 19. En la figura, ∆ABC y ∆DBC están en la misma base BC. Si AD y BC se cortan en O, demuestre que 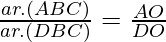$\frac{ar.(∆ABC)}{ar.(∆DBC)}=\frac{AO}{DO}$

Solución:

Dado que dos ∆ABC y ∆DBC están en la misma base BC como se muestra en la figura dada

AC y BD se intersecan en O

Ahora dibuja AL ⊥ BC y DM ⊥BC

Demostrar: $\frac{ar.(∆ABC)}{ar.(∆DBC)}=\frac{AO}{DO}$

Prueba:

En ∆ALO y ∆DMO,

∠L =∠M = 90°

∠AOL = ∠DOM [Ángulos verticalmente opuestos]

Entonces, por AA, ∆ALO ∼ ∆DMO

Entonces, AL/DM = AO/DO

Ahora $\frac{ar(∆ABC)}{ar(∆DBC)}=\frac{\frac{1}{2}BC×AL}{\frac{1}{2}BC×DM}=\frac{AL}{DM}$

Pero AL/DM = AO/DO (Probado arriba)

Asi que, $\frac{ar.(∆ABC)}{ar.(∆DBC)}=\frac{AO}{DO}$

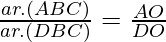
Por lo tanto probado

Pregunta 20. ABCD es un trapecio en el que AB || CD. Las diagonales AC y BD se cortan en O. Demuestra que

(i) ∆AOB ~ ∆COD

(ii) Si OA = 6 cm, OC = 8 cm, encuentre

(a)ar(∆AOB)/ar(∆COD) (b)ar(∆AOD)/ar(∆COD)

Solución:

Dado que ABCD es un trapecio en el que AB || CD y las diagonales AC y BD se cortan en O

Ahora, en la figura del punto D, dibuja DL⊥AC

(i) En ∆AOB y ∆COD

∠AOB =∠COD [Ángulos verticalmente opuestos]

∠OAB =∠OCD [Ángulos alternos]

Entonces, por el criterio de AA

∆AOB ~ ∆COD

(ii) Dado que OA = 6 cm, OC = 8 cm

Como sabemos que ∆AOB ~ ∆COD

Entonces, OA/OC = OB/OD = AB/CD

(a) ar(∆AOB)/ar(∆COD) = AO ² /OC ²

= 6 ² /8 ² = 36/64 = 9/16

Por tanto, ar(∆AOB)/ar(∆COD) = 9/16

(b) Como sabemos que ∆AOD y ∆COD tienen sus bases en la misma línea y su vértice A es común

Por tanto, ar(∆AOD)/ar(∆COD) = AO/OC = 6/8 = 3/4

Pregunta 21. En ∆ABC, P divide al lado AB tal que AP : PB = 1 : 2. Q es un punto en AC tal que PQ || ANTES DE CRISTO. Encuentra la razón de las áreas de ∆APQ y el trapecio BPQC.

Solución:

Dado que ABC es un triángulo, en el que P divide al lado AB tal que

AP : PB = 1 : 2. Q es un punto en AC tal que PQ || antes de Cristo

En ∆APQ y ∆ABC

∠APQ = ∠B

∠PAQ = ∠BAC

Entonces, por el criterio de AA

∆APQ ∼ ∆ABC

Asi que,

ar(∆APQ)/ar(∆ABC) = (AP) ² /(AB) ²

ar(∆APQ)/ar(∆ABC) = (1) ² /(1 + 2) ² = (1) ² /(3) ² = 1/9

9 ar(∆APQ) = ar(∆ABC)

9 ar(∆APQ) = ar(∆APQ) + ar(trampa. BPQC)

9 ar(∆APQ) = ar(trampa BPQC)

ar(∆APQ)/ar(trampa BPQC) = 1/9

Por lo tanto, la relación de las áreas de ∆APQ y el trapecio BPQC es 1:9

Pregunta 22. AD es una altura de un triángulo equilátero ABC. Sobre AD como base se construye otro triángulo equilátero ADE. Demostrar que Área (∆ADE) : Área (∆ABC) = 3 : 4.

Solución:

Dado que AD es una altura de un triángulo equilátero ABC.

Sobre AD como base se construye otro triángulo equilátero ADE

Demostrar: Área (∆ADE) : Área (∆ABC) = 3 : 4

Prueba:

Área de ∆ABC = √3/4 BC ²

y AD = √3/2 BC

Área de ∆ADE = √3/4 AD ²

= √3/4 (√3/2 aC) ² = 3√3/16 aC ²

Entonces, la razón del área (∆ADE):área (∆ABC) = 3√3/16 BC ² : √3/4 BC ²

= 3/4:1 = 3:4

Publicación traducida automáticamente

Artículo escrito por ysachin2314 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 10 Soluciones RD Sharma – Capítulo 4 Triángulos – Ejercicio 4.6 | conjunto 2

Pregunta 11. Las áreas de dos triángulos semejantes son 121 cm ² y 64 cm ² respectivamente. Si la mediana del primer triángulo es de 12,1 cm, encuentra la mediana correspondiente del otro.

Pregunta 12. En ∆ABC ~ ∆DEF tal que AB = 5 cm y (∆ABC) = 20 cm ² y área (∆DEF) = 45 cm ² , determine DE.

Pregunta 13. En ∆ABC, PQ es un segmento de línea que corta a AB en P y AC en Q tal que PQ || BC y PQ dividen ∆ABC en dos partes de igual área. Encuentre BP/AB.

Pregunta 14. Las áreas de dos triángulos semejantes ABC y PQR están en la razón 9 : 16. Si BC = 4,5 cm, encuentra la longitud de QR.

Pregunta 15. ABC es un triángulo y PQ es una recta que corta a AB en P y a AC en Q. Si AP = 1 cm, PB = 3 cm, AQ = 1,5 cm, QC = 4,5 cm, prueba que el área de ∆APQ es un dieciseisavo del área de ∆ABC.

Pregunta 16. Si D es un punto del lado AB de ∆ABC tal que AD : DB = 3 : 2 y E es un punto de BC tal que DE || C.A. Encuentra la razón de las áreas de ∆ABC y ∆BDE.

Pregunta 17. Si ∆ABC y ∆BDE son triángulos equiláteros, donde D es el punto medio de BC, encuentra la razón de las áreas de ∆ABC y ∆BDE.

Pregunta 18. Dos triángulos isósceles tienen ángulos verticales iguales y sus áreas están en la razón 36 : 25. Encuentra la razón de sus alturas correspondientes.

Pregunta 19. En la figura, ∆ABC y ∆DBC están en la misma base BC. Si AD y BC se cortan en O, demuestre que $\frac{ar.(∆ABC)}{ar.(∆DBC)}=\frac{AO}{DO}$

Pregunta 20. ABCD es un trapecio en el que AB || CD. Las diagonales AC y BD se cortan en O. Demuestra que

(i) ∆AOB ~ ∆COD

(ii) Si OA = 6 cm, OC = 8 cm, encuentre

(a)ar(∆AOB)/ar(∆COD) (b)ar(∆AOD)/ar(∆COD)

Pregunta 21. En ∆ABC, P divide al lado AB tal que AP : PB = 1 : 2. Q es un punto en AC tal que PQ || ANTES DE CRISTO. Encuentra la razón de las áreas de ∆APQ y el trapecio BPQC.

Pregunta 22. AD es una altura de un triángulo equilátero ABC. Sobre AD como base se construye otro triángulo equilátero ADE. Demostrar que Área (∆ADE) : Área (∆ABC) = 3 : 4.

Deja una respuesta Cancelar la respuesta

Pregunta 11. Las áreas de dos triángulos semejantes son 121 cm 2 y 64 cm 2 respectivamente. Si la mediana del primer triángulo es de 12,1 cm, encuentra la mediana correspondiente del otro.

Pregunta 12. En ∆ABC ~ ∆DEF tal que AB = 5 cm y (∆ABC) = 20 cm 2 y área (∆DEF) = 45 cm 2 , determine DE.

Pregunta 13. En ∆ABC, PQ es un segmento de línea que corta a AB en P y AC en Q tal que PQ || BC y PQ dividen ∆ABC en dos partes de igual área. Encuentre BP/AB.

Pregunta 14. Las áreas de dos triángulos semejantes ABC y PQR están en la razón 9 : 16. Si BC = 4,5 cm, encuentra la longitud de QR.

Pregunta 15. ABC es un triángulo y PQ es una recta que corta a AB en P y a AC en Q. Si AP = 1 cm, PB = 3 cm, AQ = 1,5 cm, QC = 4,5 cm, prueba que el área de ∆APQ es un dieciseisavo del área de ∆ABC.

Pregunta 16. Si D es un punto del lado AB de ∆ABC tal que AD : DB = 3 : 2 y E es un punto de BC tal que DE || C.A. Encuentra la razón de las áreas de ∆ABC y ∆BDE.

Pregunta 17. Si ∆ABC y ∆BDE son triángulos equiláteros, donde D es el punto medio de BC, encuentra la razón de las áreas de ∆ABC y ∆BDE.

Pregunta 18. Dos triángulos isósceles tienen ángulos verticales iguales y sus áreas están en la razón 36 : 25. Encuentra la razón de sus alturas correspondientes.

Pregunta 19. En la figura, ∆ABC y ∆DBC están en la misma base BC. Si AD y BC se cortan en O, demuestre que

Pregunta 20. ABCD es un trapecio en el que AB || CD. Las diagonales AC y BD se cortan en O. Demuestra que

(i) ∆AOB ~ ∆COD

(ii) Si OA = 6 cm, OC = 8 cm, encuentre

(a)ar(∆AOB)/ar(∆COD) (b)ar(∆AOD)/ar(∆COD)

Pregunta 21. En ∆ABC, P divide al lado AB tal que AP : PB = 1 : 2. Q es un punto en AC tal que PQ || ANTES DE CRISTO. Encuentra la razón de las áreas de ∆APQ y el trapecio BPQC.

Pregunta 22. AD es una altura de un triángulo equilátero ABC. Sobre AD como base se construye otro triángulo equilátero ADE. Demostrar que Área (∆ADE) : Área (∆ABC) = 3 : 4.

Deja una respuesta Cancelar la respuesta

Pregunta 11. Las áreas de dos triángulos semejantes son 121 cm ² y 64 cm ² respectivamente. Si la mediana del primer triángulo es de 12,1 cm, encuentra la mediana correspondiente del otro.

Pregunta 12. En ∆ABC ~ ∆DEF tal que AB = 5 cm y (∆ABC) = 20 cm ² y área (∆DEF) = 45 cm ² , determine DE.

Pregunta 19. En la figura, ∆ABC y ∆DBC están en la misma base BC. Si AD y BC se cortan en O, demuestre que $\frac{ar.(∆ABC)}{ar.(∆DBC)}=\frac{AO}{DO}$