Clase 10 Soluciones RD Sharma – Capítulo 4 Triángulos – Ejercicio 4.6

Pregunta 1. Los triángulos ABC y DEF son semejantes.

(i) Si el área (△ABC) = 16 cm ² , el área (△DEF) = 25 cm ² y BC = 2,3 cm, encuentre EF.

Solución:

Dado que, △ABC ∼ △DEF,

Asi que,

ar.(△ACB)/ar.(△DEF) = (BC) ² /(EF) ²

16/25 = (2.3) ² /FE ²

(4) ² /(5) ² = (2.3) ² /FE ²

4/5 = 2,3/EF

FE = (2,3 × 5)/4

FE = 11,5/4 = 2,875 cm

Por lo tanto, FE = 2,875 cm

(ii) Si el área (△ABC) = 9 cm ² , el área (△DEF) = 64 cm ² y DE = 5,1 cm, encuentre AB.

Solución:

Dado que, △ABC ∼ △DEF

Asi que,

ar.(△ACB)/ar.(△DEF) = (AB) ² /(DE) ²

9/5 = AB ² /(5.1) ²

(3) ² /(8) ² = AB ² /(5.1) ²

3/8 = AB/5.1

AB = (3 × 5,1)/8 = 15,3/8

Por lo tanto, AB = 1,9125 cm

(iii) Si AC = 19 cm y DF = 8 cm, encuentre la razón del área de dos triángulos.

Solución:

Dado que, △ABC ∼ △DEF

Asi que,

ar.(△ACB)/ar.(△DEF) = (AB) ² /(DE) ²

= (19)/(8) ² = 361/64

Por lo tanto, ar.(△ABC):ar.(△DEF) = 361:64

(iv) Si el área (△ABC) = 36 cm ² , el área (△DEF) = 64 cm ² y DE = 6,2 cm, encuentre AB.

Solución:

Dado que, △ABC ∼ △DEF

Asi que,

ar.(△ACB)/ar.(△DEF) = (AB) ² /(DE) ²

⇒ 36/64 = AB ² /(6.2) ²

⇒ 6/8=AB/(6.2)

⇒ AB/6.2 = 6/8

⇒ AB = (6 × 6,2)/8 = 37,2/8

AB = 4,65

Por lo tanto AB = 4,65 cm

(v) Si AB = 1,2 cm y DE = 1,4 cm, encuentre la razón de las áreas de △ABC y △DEF.

Solución:

Dado que, △ABC ∼ △DEF

Asi que,

ar.(△ACB)/ar.(△DEF) = (AB) ² /(DE) ²

(1,2) ² /( 1,4) ² = 1,44/1,96 = 144/196 = 36/49

Por lo tanto, ar.(△ABC):ar.(△DEF) = 36:49

Pregunta 2. En la fig. por debajo de ∆ACB ~ ∆APQ. Si BC = 10 cm, PQ = 5 cm, BA = 6,5 cm y AP = 2,8 cm, encuentre CA y AQ. Además, encuentra el área (∆ACB): área (∆APQ).

Solución:

Según la pregunta

Se da que, BC = 10 cm, PQ = 5 cm, BA = 6,5 cm y AP = 2,8 cm

Además, △ACB ∼ △APQ

Entonces, BC/PQ = AB/AQ = AC/AP

10/5 = 6,5/AQ = CA/2,8

6.5/CA = 10/5

⇒ AQ = (6,5 × 5)/10 = 3,25

y AC/2.8 = 10/5

⇒ (2,8 × 10)/5 = 5,6

CA = 5,6 m, AQ = 3,25 cm

Como sabemos que △ACB ∼ △APQ,

Entonces, ar.(△ACB)/ar.(△APQ) = (BC) ² /(PQ) ²

ar.(△ACB)/ar.(△APQ) = (10) ² /(5) ² = 100/25 = 4/1

Por lo tanto, ar(△ACB):ar(△APQ) = 4:1

Pregunta 3. Las áreas de dos triángulos semejantes son 81 cm ² y 49 cm ² respectivamente. Encuentra la razón de sus alturas correspondientes. ¿Cuál es la razón de sus medianas correspondientes?

Solución:

Consideremos dos triángulos semejantes, ABC y PQR cuyas alturas son AD y PO

Se sabe que las áreas de dos triángulos semejantes son 81 cm ² y 49 cm ²

Entonces, △ABC = 81 cm ² y △PQR = 49 cm ²

Entonces, ar.(△ABC)/ar.(△PQR) = (AB) ² /(PQ) ²

81/49 = (AB/PQ) ²

9/7 = AB/PQ

Ahora, en △ABD y △PQO

∠B = ∠Q

∠ADB = ∠POQ = 90°

Por lo tanto, △ABD ~ △PQO

Entonces, AB/PQ = AD/PO

Por lo tanto, AD/PO = 9/7

O

DA:PO = 9:7

Como sabemos, que la razón de las áreas de dos triángulos semejantes es proporcional al cuadrado de sus correspondientes alturas y también a los cuadrados de sus correspondientes medianas.

Entonces, la razón en sus medianas = 9 : 7

Pregunta 4. Las áreas de dos triángulos semejantes son 169 cm ² y 121 cm ² respectivamente. Si el lado más largo del triángulo más grande mide 26 cm, encuentra el lado más largo del triángulo más pequeño.

Solución:

Dado que ambos triángulos son semejantes

Entonces, el área del triángulo más grande (ABC) = 169 cm ²

y área del triángulo más pequeño (PQR) = 121 cm ²

La longitud de los lados más largos de los triángulos más grandes (AC) = 26 cm

Supongamos que la longitud del lado más largo del triángulo más pequeño (PR) = x

Entonces, el ar.(△ABC)/ar.(△PQR) = (AC) ² /(PR) ²

169/121 = (26) ² /(x) ²

13/11 = 26/x

x = (13 × 26)/11

x = 22

Por lo tanto, la longitud del lado más largo del triángulo más pequeño es de 22 cm.

Pregunta 5. Las áreas de dos triángulos semejantes son 25 cm ² y 36 cm ² respectivamente. Si la altura del primer triángulo es de 2,4 cm, encuentra la altura correspondiente del otro.

Solución:

Dado que, el área del primer triángulo = 25 cm ²

y el área de la segunda = 36 cm ²

Altitud del primer triángulo = 2,4 cm

Consideremos la altura del segundo triángulo = x

Se da que ambos triángulos son semejantes, entonces

ar.(primer triángulo)/ar.(segundo triángulo) = (Altitud del primer triángulo) ² /(Altitud del segundo triángulo) ²

⇒ 25/36 = (2,4) ² /x ²

⇒ 2,4/x = 5/6

⇒ x = (2,4 × 6)/5 = 14,4/5 = 2,88

Por lo tanto, la altura del segundo triángulo es de 2,88 cm.

Pregunta 6. Las alturas correspondientes de dos triángulos semejantes son 6 cm y 9 cm respectivamente. Halla la razón de sus áreas.

Solución:

Dado que la longitud de la altura correspondiente de dos triángulos es de 6 cm y 9 cm

Además, ambos triángulos son semejantes.

Asi que,

ar.(primer triángulo)/ar.(segundo triángulo) = (6) ² /(9) ²

= 36/81

= 4/9

Por lo tanto, la razón de las áreas de los triángulos es 4:9

Pregunta 7. ABC es un triángulo en el que ∠A =90°, AN⊥ BC, BC = 12 cm y AC = 5cm. Encuentra la razón de las áreas de ∆ANC y ∆ABC.

Solución:

Dado que,

En ∆ABC, ∠A = 90°

AN ⊥ BC

BC = 12 cm, AC = 5 cm

Entonces, en ∆ANC y ∆ ABC,

∠ANC = ∠BAC = 90°

∠C =∠C [Común]

Entonces, por AA,

∆ANC ∼ ∆ABC

ar.(∆ANC)/ar.(∆ABC) = (AC) ² /(BC) ² = (5) ² /(12) ² = 25/144

Por lo tanto, la razón de las áreas de ∆ANC y ∆ABC es 25:144

Pregunta 8. En la Fig., DE || antes de Cristo

(i) Si DE = 4 cm, BC = 6 cm y Área (∆ADE) = 16 cm ² , encuentre el área de ∆ABC.

(ii) Si DE = 4 cm, BC = 8 cm y Área (∆ADE) = 25 cm ² , encuentre el área de ∆ABC.

(iii) Si DE : BC = 3 : 5. Calcular la razón de las áreas de ∆ADE y el trapecio BCED.

Solución:

Dado eso, DE || antes de Cristo

Entonces, en ∆ADE y ∆ABC

∠ADE = ∠B

∠BAC = ∠DAE

Entonces, por AA

∆ADE ~ ∆ABC

(i) Dado que DE = 4 cm, BC = 6 cm y ar(∆ADE) = 16 cm ²

Como sabemos que ∆ADE ∼ ∆ABC

Entonces, ar(∆ADE)/ar(∆ABC) = DE ² /BC ²

16/ar(∆ABC) = 4 ² /6 ² = 16/36

Entonces, 16 × área ∆ABC = 16 × 36

⇒ ar.(∆ABC) = 36cm ²

(ii) Dado que DE = 4 cm, BC = 8 cm y ar(∆ADE) = 25 cm ²

Como sabemos que ∆ADE ∼ ∆ABC

Entonces, ar(∆ADE)/ar(∆ABC) = DE ² /BC ²

25/área(∆ABC) = (4) ² /(8) ² = 16/64

área(∆ABC) = (25 × 64)/16 = 100 cm ²

(iii) Dado que, DE : BC = 3 : 5

Como sabemos que ∆ADE ∼ ∆ABC

área(∆ADE)/área(∆ABC) = DE ² /BC ² = (3/5) ² = 9/25

25 (área(∆ADE)) = 9 (área ∆ABC)

25 (área(∆ADE)) = 9(área ∆ADE + área trapecio BCED)

área(∆ADE)/área del trapecio BCED = 9/16

Por tanto, la razón de las áreas de ∆ADE y el trapecio BCED es 9:16

Pregunta 9. En ∆ABC, D y E son los puntos medios de AB y AC respectivamente. Encuentra la razón de las áreas de ∆ADE y ∆ABC.

Solución:

Dado que, en ∆ABC, D y E son los puntos medios de AB y AC

Entonces, DE||BC y DE = 1/2BC

En ∆ADE y ∆ABC,

∠ADE = ∠B

∠DAE = ∠BAC [Común]

por AA

∆ADE ∼ ∆ABC

Entonces, ar(∆ADE)/ar(∆ABC) = (DE) ² /(BC) ² $=\frac{(\frac{1}{2}BC)^2}{BC^2}\\ =\frac{1×BC^2}{4BC^2}=\frac{1}{4}$

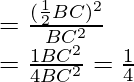
Por lo tanto, la razón de las áreas de ∆ADE y ∆ABC es 1:4

Pregunta 10. Las áreas de dos triángulos semejantes son 100 cm ² y 49 cm ² respectivamente. Si la altura del triángulo mayor es de 5 cm, encuentre la altura correspondiente del otro.

Solución:

Consideremos ∆ABC y ∆DEF

Se da que, área ∆ABC = 100 cm ²

y área ∆DEF = 49 cm ²

AL perpendicular BC y DM/EF

AL = 5 cm,

Sea DM = x cm

Se da que ∆ABC ~ ∆DEF

Entonces, ar(∆ABC)/ar(∆DEF) = AL ² /DM ²

100/49 = (5) ² /(x) ²

100/49 = 25/ ^x2

x2 ⁼ (25 × 49)/100 = 49/4

x = $\sqrt{\frac{49}{4}}=\frac{7}{2}=3.5$

Por lo tanto, la longitud de la altura del segundo triángulo es de 3,5 cm.

Publicación traducida automáticamente

Artículo escrito por ysachin2314 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 10 Soluciones RD Sharma – Capítulo 4 Triángulos – Ejercicio 4.6 | Serie 1

Pregunta 1. Los triángulos ABC y DEF son semejantes.

(i) Si el área (△ABC) = 16 cm ² , el área (△DEF) = 25 cm ² y BC = 2,3 cm, encuentre EF.

(ii) Si el área (△ABC) = 9 cm ² , el área (△DEF) = 64 cm ² y DE = 5,1 cm, encuentre AB.

(iii) Si AC = 19 cm y DF = 8 cm, encuentre la razón del área de dos triángulos.

(iv) Si el área (△ABC) = 36 cm ² , el área (△DEF) = 64 cm ² y DE = 6,2 cm, encuentre AB.

(v) Si AB = 1,2 cm y DE = 1,4 cm, encuentre la razón de las áreas de △ABC y △DEF.

Pregunta 2. En la fig. por debajo de ∆ACB ~ ∆APQ. Si BC = 10 cm, PQ = 5 cm, BA = 6,5 cm y AP = 2,8 cm, encuentre CA y AQ. Además, encuentra el área (∆ACB): área (∆APQ).

Pregunta 3. Las áreas de dos triángulos semejantes son 81 cm ² y 49 cm ² respectivamente. Encuentra la razón de sus alturas correspondientes. ¿Cuál es la razón de sus medianas correspondientes?

Pregunta 4. Las áreas de dos triángulos semejantes son 169 cm ² y 121 cm ² respectivamente. Si el lado más largo del triángulo más grande mide 26 cm, encuentra el lado más largo del triángulo más pequeño.

Pregunta 5. Las áreas de dos triángulos semejantes son 25 cm ² y 36 cm ² respectivamente. Si la altura del primer triángulo es de 2,4 cm, encuentra la altura correspondiente del otro.

Pregunta 6. Las alturas correspondientes de dos triángulos semejantes son 6 cm y 9 cm respectivamente. Halla la razón de sus áreas.

Pregunta 7. ABC es un triángulo en el que ∠A =90°, AN⊥ BC, BC = 12 cm y AC = 5cm. Encuentra la razón de las áreas de ∆ANC y ∆ABC.

Pregunta 8. En la Fig., DE || antes de Cristo

Pregunta 9. En ∆ABC, D y E son los puntos medios de AB y AC respectivamente. Encuentra la razón de las áreas de ∆ADE y ∆ABC.

Pregunta 10. Las áreas de dos triángulos semejantes son 100 cm ² y 49 cm ² respectivamente. Si la altura del triángulo mayor es de 5 cm, encuentre la altura correspondiente del otro.

Deja una respuesta Cancelar la respuesta

Pregunta 1. Los triángulos ABC y DEF son semejantes.

(i) Si el área (△ABC) = 16 cm 2 , el área (△DEF) = 25 cm 2 y BC = 2,3 cm, encuentre EF.

(ii) Si el área (△ABC) = 9 cm 2 , el área (△DEF) = 64 cm 2 y DE = 5,1 cm, encuentre AB.

(iii) Si AC = 19 cm y DF = 8 cm, encuentre la razón del área de dos triángulos.

(iv) Si el área (△ABC) = 36 cm 2 , el área (△DEF) = 64 cm 2 y DE = 6,2 cm, encuentre AB.

(v) Si AB = 1,2 cm y DE = 1,4 cm, encuentre la razón de las áreas de △ABC y △DEF.

Pregunta 2. En la fig. por debajo de ∆ACB ~ ∆APQ. Si BC = 10 cm, PQ = 5 cm, BA = 6,5 cm y AP = 2,8 cm, encuentre CA y AQ. Además, encuentra el área (∆ACB): área (∆APQ).

Pregunta 3. Las áreas de dos triángulos semejantes son 81 cm 2 y 49 cm 2 respectivamente. Encuentra la razón de sus alturas correspondientes. ¿Cuál es la razón de sus medianas correspondientes?

Pregunta 4. Las áreas de dos triángulos semejantes son 169 cm 2 y 121 cm 2 respectivamente. Si el lado más largo del triángulo más grande mide 26 cm, encuentra el lado más largo del triángulo más pequeño.

Pregunta 5. Las áreas de dos triángulos semejantes son 25 cm 2 y 36 cm 2 respectivamente. Si la altura del primer triángulo es de 2,4 cm, encuentra la altura correspondiente del otro.

Pregunta 6. Las alturas correspondientes de dos triángulos semejantes son 6 cm y 9 cm respectivamente. Halla la razón de sus áreas.

Pregunta 7. ABC es un triángulo en el que ∠A =90°, AN⊥ BC, BC = 12 cm y AC = 5cm. Encuentra la razón de las áreas de ∆ANC y ∆ABC.

Pregunta 8. En la Fig., DE || antes de Cristo

Pregunta 9. En ∆ABC, D y E son los puntos medios de AB y AC respectivamente. Encuentra la razón de las áreas de ∆ADE y ∆ABC.

Pregunta 10. Las áreas de dos triángulos semejantes son 100 cm 2 y 49 cm 2 respectivamente. Si la altura del triángulo mayor es de 5 cm, encuentre la altura correspondiente del otro.

Deja una respuesta Cancelar la respuesta

(i) Si el área (△ABC) = 16 cm ² , el área (△DEF) = 25 cm ² y BC = 2,3 cm, encuentre EF.

(ii) Si el área (△ABC) = 9 cm ² , el área (△DEF) = 64 cm ² y DE = 5,1 cm, encuentre AB.

(iv) Si el área (△ABC) = 36 cm ² , el área (△DEF) = 64 cm ² y DE = 6,2 cm, encuentre AB.

Pregunta 3. Las áreas de dos triángulos semejantes son 81 cm ² y 49 cm ² respectivamente. Encuentra la razón de sus alturas correspondientes. ¿Cuál es la razón de sus medianas correspondientes?

Pregunta 4. Las áreas de dos triángulos semejantes son 169 cm ² y 121 cm ² respectivamente. Si el lado más largo del triángulo más grande mide 26 cm, encuentra el lado más largo del triángulo más pequeño.

Pregunta 5. Las áreas de dos triángulos semejantes son 25 cm ² y 36 cm ² respectivamente. Si la altura del primer triángulo es de 2,4 cm, encuentra la altura correspondiente del otro.

Pregunta 10. Las áreas de dos triángulos semejantes son 100 cm ² y 49 cm ² respectivamente. Si la altura del triángulo mayor es de 5 cm, encuentre la altura correspondiente del otro.