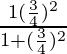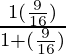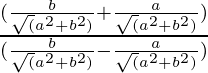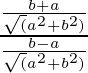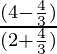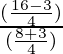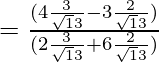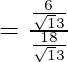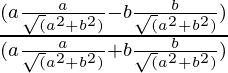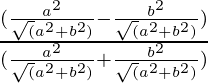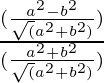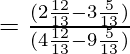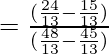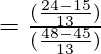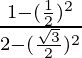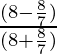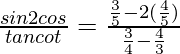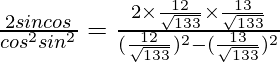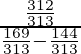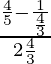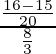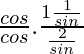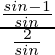Pregunta 7. Si cotθ = 7/8, evalúa:
(i) 
(ii) cuna 2 θ
Solución:
cotθ = 7/8 = Base/Perpendicular
En ángulo recto ΔPQR,
∠Q = 90°, PQ = 8, RQ = 7
Usando el teorema de Pitágoras
PR 2 = PQ 2 + QR 2
RP 2 = 8 2 + 7 2 = 64 + 49
RP 2 = 113
RP = √113
Ahorasinθ = Perpendicular/Hipotenusa = PQ/PR = 8/√113
cosθ = Base/Hipotenusa = QR/PR = 7/√113
(i)
Poniendo los valores de senθ y cosθ en la ecuación
=
=
= 49/64
(ii) cuna 2 θ
= (cosθ/senθ) 2
Poniendo los valores de sinθ y cosθ en la siguiente ecuación
=
=
= 49/64
o
cuna 2 θ = (cotθ) 2 = (7/8) 2 = 49/64
Pregunta 8. Si 3 cot A = 4, marca si 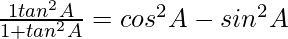 es o no.
es o no.
Solución:
Dado, 3cot A = 4 o cot A = 4/3
Dibuja un △ ABC donde ∠B = 90°, AB = 4, BC = 3
Usando el teorema de Pitágoras
CA 2 = AB 2 + BC 2
CA 2 = 4 2 + 3 2 = 16 + 9
CA 2 = 25
CA = 5
Ahora,
Tomando LHS
=
=
=
=
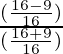
= 7/25
Tomando RHS
= cos 2 A – sen 2 A
=(
=(
=(
= 7/25
RHS = LHS (por lo tanto probado)
Pregunta 9. Si tanθ = a/b, encuentra el valor de 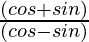
Solución:
Dado, tanθ = a/b
Dibujar un △ABC donde ∠B = 90°, AB = b, BC = a
Usando el teorema de Pitágoras
AC 2 = BC 2 + AB 2
CA 2 = un 2 + segundo 2
CA 2 =
Ahora,
=
=
= (b + a)/(b – a)
Pregunta 10. Si 3tanθ = 4, encuentra el valor de 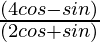
Solución:
Dado tanθ = 4/3
Ahora, dividiendo el numerador y denominador por cosθ
=
Poniendo los valores de tanθ en la ecuación anterior
=
=
= 8/10
= 4/5
Pregunta 11. Si 3cotθ = 2, encuentra el valor de 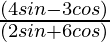
Solución:
Dado: 3cotθ = 2
Usando el teorema de Pitágoras
AC 2 = BC 2 + AB 2
CA 2 = 3 2 + 4 2
CA 2 = 9 + 16 = 25
CA = 5
Ahora,
=
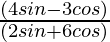

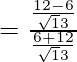
= 6/18 = 1/3
Pregunta 12. Si tanθ = a/b, demuestre que 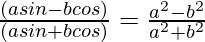
Solución:
Dado, tanθ = a/b
Usando el teorema de Pitágoras
AC 2 = BC 2 + AB 2
CA 2 = un 2 + segundo 2
CA 2 =
Ahora,
=
Poniendo los valores de sinθ y cosθ en la ecuación anterior
=
=
=
=
Por lo tanto probado
Pregunta 13. Si secθ = 13/5, prueba que 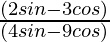 =3
=3
Solución:
Dado, secθ = 13/5
Usando el teorema de Pitágoras
AC 2 = BC 2 + AB 2
13 2 = BC 2 + 5 2
2 aC = 169 – 25 = 144
BC = 12
Ahora,
Tomando LHS
=
Poniendo los valores de sinθ y cosθ en la ecuación anterior
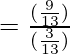
= 3 = lado derecho
Por lo tanto probado
Pregunta 14. Si cosθ = 12/13, demuestre que senθ(1 – tanθ) = 35/156
Solución:
Tenemos cosθ = 12/13
Usando el teorema de Pitágoras
AC 2 = BC 2 + AB 2
13 2 = BC 2 + 12 2
2 aC = 169 – 144 = 25
BC = 5
Ahora,
Tomando LHS
= sinθ(1 – tanθ)
=
=
= 35/156
= lado derecho
Por lo tanto probado
Pregunta 15. Si cotθ = 1/√3, demuestre que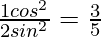
Solución:
Dado, cotθ = 1/√3
tanθ = 1/cotθ =√3
Del teorema de Pitágoras,
CA 2 = AB 2 + BC 2
CA 2 = 1 2 + (√3) 2
CA 2 = 3 + 1 = 4
CA = 2
Ahora,
Tomando LHS
=
=
= 3/5
Por lo tanto probado
Pregunta 16. Si tanθ = 1/√7, entonces 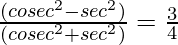
Solución:
Tenemos
tanθ = 1/√7
cotθ = √7
Sabemos sec 2 θ = (1 + tan 2 θ) = 1 + 1/7 = 8/7
y cosec 2 θ = (1 + cot 2 θ) = 1 + 7 = 8
Ahora,
=
= 48/64 = 3/4
Pregunta 17. Si secθ = 5/4, encuentra el valor de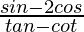
Solución:
Dado:
secθ = 5/4
cosθ = 1/segθ = 4/5
Del teorema de Pitágoras,
AC 2 = BC 2 + AB 2
5 2 = BC 2 + 4 2
BC 2 = 25 − 16 = 9
BC = 3
Ahora,
=
=
= 12/7
Pregunta 18. Si tanθ = 12/13, encuentre el valor de 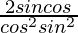
Solución:
Dado: tanθ = 12/13
Del teorema de Pitágoras,
AC 2 = BC 2 + AB 2
CA 2 = (13) 2 + (12) 2
CA 2 = 313
CA = √313
senθ = 12/√313
cosθ = 13/√313
Tenemos
= \
=
= 312/25
Pregunta 19. Si cosθ = 3/5, entonces evalúa 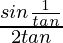
Solución:
Dado:
cosθ = 3/5
Del teorema de Pitágoras,
AC 2 = BC 2 + AB 2
5 2 = 3 2 + AB 2
AB 2 = 25 − 9 = 16
AB = 4
Ahora
=
=
=
= (1/20) × (3/8)
= 3/160
Pregunta 20 . Si senθ = 3/5, entonces evalúe 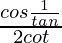
Solución:
Dado,
senθ = 3/5
Ahora
=
=
=
=
=
= (senθ – 1)/(2)
Poniendo el valor de senθ, obtenemos
=
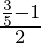
=
= -1/5
Pregunta 21. Si tanθ = 24/7, encuentra que senθ + cosθ.
Solución:
Dado:
tanθ = 24/7
Del teorema de Pitágoras,
AC 2 = BC 2 + AB 2
CA 2 = 24 2 + 7 2
CA 2 = 576 + 49 = 625
CA = 25
Ahora,
= senθ + cosθ
= 24/25 + 7/25
= (24 + 7)/25
= 31/25
Publicación traducida automáticamente
Artículo escrito por rahulsharma1771996 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

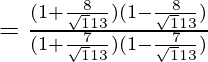
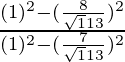
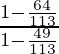

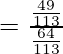
![Rendered by QuickLaTeX.com [\frac{(\frac{7}{\sqrt113})}{(\frac{8}{\sqrt113})}]^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0a3bb177c0f2fc83eb32cfe16c331859_l3.png)