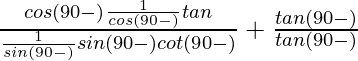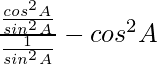Clase 10 Soluciones RD Sharma – Capítulo 5 Razones trigonométricas – Ejercicio 5.3

Pregunta 8. Demuestre lo siguiente:

(i) sen θ sen (90° – θ) – cosθ cos (90° – θ) = 0

Solución:

Tenemos que demostrar que sen θ sen (90° – θ) – cosθ cos (90° – θ) = 0

Tomando LHS

= sen θ sen (90° – θ) – cosθ cos (90° – θ) -(∵ sen (90° – θ) = cos θ)

= senθ cosθ – cosθ senθ

= 0

LHS = RHS

Por lo tanto probado

(ii) 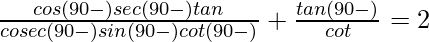$\frac{cos (90°-θ)sec (90°-θ)tanθ}{cosec(90°-θ)sin (90°-θ)cot(90°-θ)}+\frac{tan(90°-θ)}{cotθ}=2$

Solución:

Tenemos que demostrar que $\frac{cos (90°-θ)sec (90°-θ)tanθ}{cosec(90°-θ)sin (90°-θ)cot(90°-θ)}+\frac{tan(90°-θ)}{cotθ}=2$

Tomando LHS

= $\frac{cos (90°-θ)sec (90°-θ)tanθ}{cosec(90°-θ)sin (90°-θ)cot(90°-θ)}+\frac{tan(90°-θ)}{cotθ}$

= $\frac{cos (90°-θ)\frac{1}{cos (90°-θ)}tanθ}{\frac{1}{sin(90°-θ)}sin (90°-θ)cot(90°-θ)}+\frac{tan(90°-θ)}{tan(90°-θ)}$

= tan θ/tan θ + cot θ/cot θ

= 1 + 1

= 2

LHS = RHS

Por lo tanto probado

(iii) 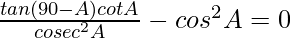$\frac{tan (90°-A)cot A}{cosec^2A} -cos^2A=0$

Solución:

Tenemos que demostrar que $\frac{tan (90°-A)cot A}{cosec^2A} -cos^2A=0$

Tomando LHS

= $\frac{cot A cot A}{cosec^2A} - cos^2A$

= $\frac{cot^2A}{cosec^2A} - cos^2A$ -(∵ cot θ = cosθ/sinθ y cosecθ = 1/sinθ)

= $\frac{\frac{cos^2A}{sin^2A}}{\frac{1}{sin^2A}} - cos^2A$

= $\frac{cos^2A}{sin^2A}sin^2A-cos^2A$

= cos ² A – cos ² A

= 0

LHS = RHS

Por lo tanto probado

(iv) 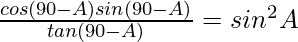$\frac{cos(90°-A)sin(90°-A)}{tan(90°-A)} = sin^2A$

Solución:

Tenemos que demostrar que $\frac{cos(90°-A)sin(90°-A)}{tan(90°-A)} = sin^2A$

Tomando LHS

= $\frac{cos(90°-A)sin(90°-A)}{tan(90°-A)}$

= $\frac{sin A cos A}{cot A}$

= $\frac{sin A cos A}{\frac{cos A}{sin A}}$

= $\frac{(sin A cos A)sin A}{cos A}$

= sen ² A

LHS = RHS

Por lo tanto probado

(v) sen (50° + θ) – cos (40° – θ) + tan 1° tan 10° tan 20° tan 70° tan 80° tan 89° = 1

Solución:

Tenemos que probar que sin (50° + θ) – cos (40° – θ) + tan 1° tan 10° tan 20° tan 70° tan 80° tan 89° = 1

Tomando LHS

= sin (50° + θ) – cos (40° – θ) + tan 1° tan 10° tan 20° tan 70° tan 80° tan 89°

= cos(90° – (50° + θ)) – coseno (40° – θ) + tan (90° – 89°) tan (90° – 80°) tan (90° – 70°) tan 70° tan 80° tan 89°

= cos (40° – θ) – cos (40° – θ) + cot 89° cot 80° cot 70° tan 70° tan 80° tan 89°

= 0 + 1 = 1

LHS = RHS

Por lo tanto probado

Pregunta 9. Evaluar:

(i) 2/3(cos ⁴ 30° – sen ⁴ 45°) – 3(sen ² 60° – sec ² 45°) + 1/4cot ² 30°

Solución:

Dado: 2/3(cos ⁴ 30° – sen ⁴ 45°) – 3(sen ² 60° – sec ² 45°) + 1/4cot ² 30°

= $\frac{2}{3}((\frac{\sqrt3}{2})^4-(\frac{1}{\sqrt2})^4)-3((\frac{\sqrt3}{2})^2-(\sqrt2)^2)+\frac{1}{4}(\sqrt3)^2$

= $\frac{2}{3}((\frac{9}{16})-(\frac{1}{4}))-3((\frac{3}{4})-(2))+\frac{3}{4}$

= 2/3(5/16) – 3(-5/4) + 3/4

= 5/24 + 90/24 + 18/24

= 113/24

Por lo tanto, 2/3(cos ⁴ 30° – sen ⁴ 45°) – 3(sen ² 60° – sec ² 45°) + 1/4cot ² 30° = 113/24

(ii) 4(sen ⁴ 30° + cos ⁴ 60°) – 2/3(sen ² 60° – cos ² 45°) + 1/2tan ² 60°

Solución:

Dado: 4(sen ⁴ 30° + cos ⁴ 60°) – 2/3(sen ² 60° – cos ² 45°) + 1/2tan ² 60°

= $4((\frac{1}{2})^4+(\frac{1}{2})^4)-\frac{2}{3}((\frac{\sqrt3}{2})^2-(\frac{1}{\sqrt2})^2)+\frac{1}{2}(\sqrt3)^2$

= $4((\frac{1}{16})+(\frac{1}{16}))-\frac{2}{3}((\frac{3}{4})-(\frac{1}{2}))+\frac{3}{2}$

= 4(2/16) – 2/3(1/4) + 3/2

= 1/2 – 1/6 + 3/2

= 4/2 – 1/6

= 2 – 1/6

= (12 – 1)/6

= 11/6

Por lo tanto, 4(sen ⁴ 30° + cos ⁴ 60°) – 2/3(sen ² 60° – cos ² 45°) + 1/2tan ² 60° = 11/6

(iii) sen 50°/cos 40° + cosec 40° / seg 50° – 4cos 50° cosec40°

Solución:

Dado: sen 50°/cos 40° + cosec 40° / seg 50° – 4cos 50° cosec40°

= $\frac{sin 50°}{cos (90° - 50°)} + \frac{cosec 40° }{ sec (90°- 40°)} - 4cos 50° cosec(90°-50°)$

= sin 50°/sin 50° + cosec 40° / cosec 40° – 4cos 50° sec50°

= 1 + 1 – 4

= -2

Por lo tanto, sen 50°/cos 40° + cosec 40° / seg 50° – 4cos 50° cosec40° = -2

(iv) tan35°tan40°tan45°tan50°tan55°

Solución:

Dado: tan35°tan40°tan45°tan50°tan55°

= bronceado(90° – 55°)bronceado(90° – 50°)bronceado45°bronceado50°bronceado55°

= cuna55°cuna50°bronceado45°bronceado50°bronceado55°

= (1/tan55°)(1/tan50°)tan45°tan50°tan55°

= 1

Por lo tanto, tan35°tan40°tan45°tan50°tan55° = 1

(v) cosec(65° + θ) – sec(25° – θ) – tan(55° – θ) + cot(35° + θ)

Solución:

Dado: cosec(65° + θ) – sec(25° – θ) – tan(55° – θ) + cot(35° + θ)

= cosec(65° + θ) – cosec(90° – (25° – θ)) – tan(55° – θ) + tan(90° – (35° + θ))

= cosec(65° + θ) – cosec(90° – 25° + θ) – tan(55° – θ) + tan(90° – 35° – θ)

= cosec(65° + θ) – cosec(65° + θ) – tan(55° – θ) + tan(55° – θ)

= 0

Por lo tanto, cosec(65° + θ) – sec(25° – θ) – tan(55° – θ) + cot(35° + θ) = 0

(vi) tan7°tan23°tan60°tan67°tan83°

Solución:

Dado: tan7°tan23°tan60°tan67°tan83°

= bronceado(90° – 83°)bronceado(90° – 67°)bronceado60°bronceado67°bronceado83°

= cuna83°cot67°bronceado60°bronceado67°bronceado83°

= (1/bronceado83°)(1/bronceado67°)bronceado60°bronceado67°bronceado83°

= tan60°

= √3

Por lo tanto, tan7°tan23°tan60°tan67°tan83° = √3

(vii) 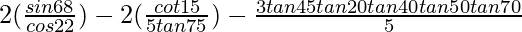$2(\frac{sin68°}{cos22°}) - 2(\frac{cot15°}{5tan75°}) - \frac{3tan45°tan20°tan40°tan50°tan70°}{5}$

Solución:

Dado: $2(\frac{sin68°}{cos22°}) - 2(\frac{cot15°}{5tan75°}) - \frac{3tan45°tan20°tan40°tan50°tan70°}{5}$

= $\frac{2sin68°}{cos(90°-68°)}-\frac{2cot15°}{5tan(90°-15°)}-\frac{(3tan45°tan(90°-70°)tan(90°-50°)tan50°tan70°)}{5}$

= $\frac{2sin68°}{sin68°} - \frac{2cot15°}{5cot15°} - \frac{(3tan45°cot70°cot50°tan50°tan70°)}{5}$

= 2 – 2/5 – 3/5

= (10 – 2 – 3)/5

= 5/5

= 1

Por lo tanto, $2(\frac{sin68°}{cos22°}) - 2(\frac{cot15°}{5tan75°}) - \frac{3tan45°tan20°tan40°tan50°tan70°}{5}$ = 1

(viii) $\frac{3cos55°}{7sin35°} - \frac{4(cos70°cosec20°)}{7(tan5°tan25°tan45°tan65°tan85°)}$

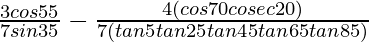
Solución:

Dado: $\frac{3cos55°}{7sin35°} - \frac{4(cos70°cosec20°)}{7(tan5°tan25°tan45°tan65°tan85°)}$

= $\frac{3cos55°}{7sin(90°-55°)}-\frac{4(cos70°cosec(90°-70°))}{7(tan(90°-85°)tan(90°-65°)tan45°tan65°tan85°})$

= $\frac{3cos55°}{7cos55°}-\frac{4(cos70°sec70°)}{7(cot85°cot65°tan45°tan65°tan85°)}$

= 3/7 – 4/7

= -1/7

Por lo tanto, $\frac{3cos55°}{7sin35°} - \frac{4(cos70°cosec20°)}{7(tan5°tan25°tan45°tan65°tan85°)}$ = -1/7

(ix) sen18°/cos72° + √3(tan10°tan30°tan40°tan50°tan80°)

Solución:

Dado: sin18°/cos72° + √3(tan10°tan30°tan40°tan50°tan80°)

= sin18°/cos(90° – 18°) + √3(tan(90° – 80°)tan(90° – 50°)tan30°tan50°tan80°)

= sin18°/sin18° + √3(cot80°cot50°tan30°tan50°tan80°)

= 1 + √3tan30°

= 1 + √3(1/√3)

= 2

Por lo tanto, sin18°/cos72° + √3(tan10°tan30°tan40°tan50°tan80°) = 2

(X) 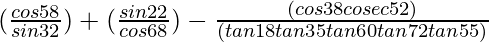$(\frac{cos58°}{sin 32°}) + (\frac{sin22°}{cos68°}) - \frac{(cos38°cosec52°)}{(tan18°tan35°tan60°tan72°tan55°)}$

Solución:

Dado: $(\frac{cos58°}{sin 32°}) + (\frac{sin22°}{cos68°}) - \frac{(cos38°cosec52°)}{(tan18°tan35°tan60°tan72°tan55°)}$

= $\frac{cos58°}{sin (90°-58°)}+\frac{sin(90°-68°)}{cos68°}-\frac{(cos38°cosec(90°-38°)}{(tan(90°-72°)tan(90°-55°)tan60°tan72°tan55°)}$

= $\frac{cos58°}{cos58°}+\frac{cos68°}{cos68°}-\frac{cos38°sec38°}{(cot72°cot55°tan60°tan72°tan55°)}$

= 1 + 1 – 1/bronceado60°

= 2 – 1/√3

= (2√3 – 1)/√3

= (6 – √3)/3

Por lo tanto, $(\frac{cos58°}{sin 32°}) + (\frac{sin22°}{cos68°}) - \frac{(cos38°cosec52°)}{(tan18°tan35°tan60°tan72°tan55°)}$ = (6 – √3)/3

Pregunta 10. Si sen θ = cos(θ − 45°), donde θ y θ−45° son ángulos agudos, encuentre la medida en grados de θ.

Solución:

Dado: sinθ = cos(θ − 45°), donde θ y θ−45° son ángulos agudos

= sinθ = cos(θ − 45°) -(∵ sinθ = cos(90 − θ))

= coseno(90° − θ) = coseno(θ − 45°)

Igualando los ángulos

(90° – θ) = (θ – 45°)

2θ = 90° + 45° = 135°

θ = 135°/2

θ = 67 $\frac{1}{2}$ °

Pregunta 11. Si A, B, C son los ángulos interiores de un triángulo ABC, demuestra que

(i) sen (B + C)/2 = cos A/2

Solución:

segun pregunta

En un triángulo ABC, A, B, C son los ángulos interiores

Entonces, la suma de los ángulos interiores = A + B + C = 180°

B +C = 180° – A

Tenemos

sen (B + C)/2 = cos A/2

Tomando LHS

pecado (B + C)/2 -(1)

Poner el valor de B + C en la ecuación (1)

= pecado (180° – A)/2

= pecado (90° – A/2)

= cos A/2

LHS = RHS

Por lo tanto probado

(ii) cos (B + C)/2 = sen A/2

Solución:

segun pregunta

En un triángulo ABC, A, B, C son los ángulos interiores

Entonces, la suma de los ángulos interiores = A + B + C = 180°

B + C = 180° – A

Tenemos

cos (B + C)/2 = sen A/2

Tomando LHS

porque (B + C)/2 -(1)

Poner el valor de B + C en la ecuación (1)

= coseno (180° – A)/2

= coseno (90° – A/2)

= sen A/2

LHS = RHS

Por lo tanto probado

Pregunta 12. Si 2θ + 45° y 30° − θ son ángulos agudos, encuentre la medida en grados de θ que satisfaga sen(2θ + 45°) = cos(30° − θ).

Solución:

Dado: 2θ + 45° y (30° − θ) son agudos y sin(2θ + 45°) = cos(30° − θ)

Tenemos,

sen(2θ + 45°) = coseno(30° − θ)

sin(2θ + 45°) = sin(90° − (30° − θ)) -(∵ cosθ = sin(90° − θ))

sen(2θ + 45°) = sen(60° + θ)

ahora igualando los angulos

2θ + 45° = 60° + θ

2θ – θ = 60° – 45°

θ = 15°

Pregunta 13. Si θ es un ángulo agudo positivo tal que secθ = cosec60°, encuentra el valor de 2cos ² θ − 1.

Solución:

Dado, θ es agudo y secθ = cosec60°

Encuentra el valor de 2cos ² θ − 1 -(1)

cosec60° = 2/√3

o secθ = 2/√3

Sabemos que, sec30° = 2/√3

secθ = sec30°

θ = 30°

Poniendo el valor de θ en la ecuación (1), obtenemos

= 2cos ² 30° − 1

= 2(√3/2) ² − 1

= 2(3/4) − 1

= 3/2 − 1

= 1/2

Por lo tanto, el valor de 2cos ² θ − 1 = 1/2

Pregunta 14. Si cos2θ = sen4θ, donde 2θ y 4θ son ángulos agudos, encuentra el valor de θ.

Solución:

Dado: 2θ y 4θ son agudos y cos2θ = sin4θ

Entonces tenemos,

cos2θ = sen(90° − 2θ) -(∵ sen (90° – θ) = cos θ)

Ahora, sen(90° − 2θ) = sen4θ

Igualando los ángulos

90° − 2θ = 4θ

90° = 2θ + 4θ

6θ = 90°

θ = 15°

Por lo tanto, el valor de θ = 15°

Pregunta 15. Si sen3θ = cos (θ − 6°), donde 3 θ y θ − 6° son agudos, encuentra el valor de θ.

Solución:

Dado: 3θ y (θ − 6°) son agudos y sen3θ = cos(θ − 6°)

Entonces tenemos,

cos(θ − 6°) = sen(90° − (θ − 6°)) = sen(96° − θ). -(∵ cosθ = sin(90° − θ))

Ahora, sin3θ = sin(96° − θ)

Igualando los ángulos

3θ = 96° − θ

3θ + θ = 96°

4θ = 96°

θ = 96°/4

θ = 24°

Por lo tanto, el valor de θ = 24°

Pregunta 16. Si sec4A = cosec(A – 20°), donde 4A es un ángulo agudo, encuentra el valor de A.

Solución:

Dado: 4A es agudo y sec4A = cosec(A − 20°)

Entonces tenemos,

sec4A = cosec(90° − 4A) -(∵ secθ = cosec(90° − θ))

Ahora, cosec(90° − 4A) = cosec(A − 20°)

Igualando los ángulos

(90° – 4A) = (A – 20°)

110° = 5A

5A = 110°

A = 110°/5

A = 22°

Por lo tanto, el valor de A = 22°

Pregunta 17. Si sec2A = cosec(A – 42°), donde 2A es un ángulo agudo, encuentra el valor de A.

Solución:

Dado: 2A es agudo y sec2A = cosec(A − 42°)

Entonces tenemos,

sec2A = cosec(90° − 2A) -(∵ secθ = cosec(90° − θ))

Ahora, cosec(90° − 2A) = cosec(A − 42°)

Igualando los ángulos

(90° – 2A) = (A – 42°)

132° = 3A

3A = 132°

A = 132°/3

A = 44°

Por lo tanto, el valor de A = 44°

Publicación traducida automáticamente

Artículo escrito por rahulsharma1771996 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 10 Soluciones RD Sharma – Capítulo 5 Razones trigonométricas – Ejercicio 5.3 | conjunto 2

Pregunta 8. Demuestre lo siguiente:

(i) sen θ sen (90° – θ) – cosθ cos (90° – θ) = 0

(ii) $\frac{cos (90°-θ)sec (90°-θ)tanθ}{cosec(90°-θ)sin (90°-θ)cot(90°-θ)}+\frac{tan(90°-θ)}{cotθ}=2$

(iii) $\frac{tan (90°-A)cot A}{cosec^2A} -cos^2A=0$

(iv) $\frac{cos(90°-A)sin(90°-A)}{tan(90°-A)} = sin^2A$

(v) sen (50° + θ) – cos (40° – θ) + tan 1° tan 10° tan 20° tan 70° tan 80° tan 89° = 1

Pregunta 9. Evaluar:

(i) 2/3(cos ⁴ 30° – sen ⁴ 45°) – 3(sen ² 60° – sec ² 45°) + 1/4cot ² 30°

(ii) 4(sen ⁴ 30° + cos ⁴ 60°) – 2/3(sen ² 60° – cos ² 45°) + 1/2tan ² 60°

(iii) sen 50°/cos 40° + cosec 40° / seg 50° – 4cos 50° cosec40°

(iv) tan35°tan40°tan45°tan50°tan55°

(v) cosec(65° + θ) – sec(25° – θ) – tan(55° – θ) + cot(35° + θ)

(vi) tan7°tan23°tan60°tan67°tan83°

(vii) $2(\frac{sin68°}{cos22°}) - 2(\frac{cot15°}{5tan75°}) - \frac{3tan45°tan20°tan40°tan50°tan70°}{5}$

(viii) $\frac{3cos55°}{7sin35°} - \frac{4(cos70°cosec20°)}{7(tan5°tan25°tan45°tan65°tan85°)}$

(ix) sen18°/cos72° + √3(tan10°tan30°tan40°tan50°tan80°)

(X) $(\frac{cos58°}{sin 32°}) + (\frac{sin22°}{cos68°}) - \frac{(cos38°cosec52°)}{(tan18°tan35°tan60°tan72°tan55°)}$

Pregunta 10. Si sen θ = cos(θ − 45°), donde θ y θ−45° son ángulos agudos, encuentre la medida en grados de θ.

Pregunta 11. Si A, B, C son los ángulos interiores de un triángulo ABC, demuestra que

(i) sen (B + C)/2 = cos A/2

(ii) cos (B + C)/2 = sen A/2

Pregunta 12. Si 2θ + 45° y 30° − θ son ángulos agudos, encuentre la medida en grados de θ que satisfaga sen(2θ + 45°) = cos(30° − θ).

Pregunta 13. Si θ es un ángulo agudo positivo tal que secθ = cosec60°, encuentra el valor de 2cos ² θ − 1.

Pregunta 14. Si cos2θ = sen4θ, donde 2θ y 4θ son ángulos agudos, encuentra el valor de θ.

Pregunta 15. Si sen3θ = cos (θ − 6°), donde 3 θ y θ − 6° son agudos, encuentra el valor de θ.

Pregunta 16. Si sec4A = cosec(A – 20°), donde 4A es un ángulo agudo, encuentra el valor de A.

Pregunta 17. Si sec2A = cosec(A – 42°), donde 2A es un ángulo agudo, encuentra el valor de A.

Deja una respuesta Cancelar la respuesta

Pregunta 8. Demuestre lo siguiente:

(i) sen θ sen (90° – θ) – cosθ cos (90° – θ) = 0

(ii)

(iii)

(iv)

(v) sen (50° + θ) – cos (40° – θ) + tan 1° tan 10° tan 20° tan 70° tan 80° tan 89° = 1

Pregunta 9. Evaluar:

(i) 2/3(cos 4 30° – sen 4 45°) – 3(sen 2 60° – sec 2 45°) + 1/4cot 2 30°

(ii) 4(sen 4 30° + cos 4 60°) – 2/3(sen 2 60° – cos 2 45°) + 1/2tan 2 60°

(iii) sen 50°/cos 40° + cosec 40° / seg 50° – 4cos 50° cosec40°

(iv) tan35°tan40°tan45°tan50°tan55°

(v) cosec(65° + θ) – sec(25° – θ) – tan(55° – θ) + cot(35° + θ)

(vi) tan7°tan23°tan60°tan67°tan83°

(vii)

(viii)

(ix) sen18°/cos72° + √3(tan10°tan30°tan40°tan50°tan80°)

(X)

Pregunta 10. Si sen θ = cos(θ − 45°), donde θ y θ−45° son ángulos agudos, encuentre la medida en grados de θ.

Pregunta 11. Si A, B, C son los ángulos interiores de un triángulo ABC, demuestra que

(i) sen (B + C)/2 = cos A/2

(ii) cos (B + C)/2 = sen A/2

Pregunta 12. Si 2θ + 45° y 30° − θ son ángulos agudos, encuentre la medida en grados de θ que satisfaga sen(2θ + 45°) = cos(30° − θ).

Pregunta 13. Si θ es un ángulo agudo positivo tal que secθ = cosec60°, encuentra el valor de 2cos 2 θ − 1.

Pregunta 14. Si cos2θ = sen4θ, donde 2θ y 4θ son ángulos agudos, encuentra el valor de θ.

Pregunta 15. Si sen3θ = cos (θ − 6°), donde 3 θ y θ − 6° son agudos, encuentra el valor de θ.

Pregunta 16. Si sec4A = cosec(A – 20°), donde 4A es un ángulo agudo, encuentra el valor de A.

Pregunta 17. Si sec2A = cosec(A – 42°), donde 2A es un ángulo agudo, encuentra el valor de A.

Deja una respuesta Cancelar la respuesta

(ii) $\frac{cos (90°-θ)sec (90°-θ)tanθ}{cosec(90°-θ)sin (90°-θ)cot(90°-θ)}+\frac{tan(90°-θ)}{cotθ}=2$

(iii) $\frac{tan (90°-A)cot A}{cosec^2A} -cos^2A=0$

(iv) $\frac{cos(90°-A)sin(90°-A)}{tan(90°-A)} = sin^2A$

(i) 2/3(cos ⁴ 30° – sen ⁴ 45°) – 3(sen ² 60° – sec ² 45°) + 1/4cot ² 30°

(ii) 4(sen ⁴ 30° + cos ⁴ 60°) – 2/3(sen ² 60° – cos ² 45°) + 1/2tan ² 60°

(vii) $2(\frac{sin68°}{cos22°}) - 2(\frac{cot15°}{5tan75°}) - \frac{3tan45°tan20°tan40°tan50°tan70°}{5}$

(viii) $\frac{3cos55°}{7sin35°} - \frac{4(cos70°cosec20°)}{7(tan5°tan25°tan45°tan65°tan85°)}$

(X) $(\frac{cos58°}{sin 32°}) + (\frac{sin22°}{cos68°}) - \frac{(cos38°cosec52°)}{(tan18°tan35°tan60°tan72°tan55°)}$

Pregunta 13. Si θ es un ángulo agudo positivo tal que secθ = cosec60°, encuentra el valor de 2cos ² θ − 1.