Clase 10 Soluciones RD Sharma – Capítulo 5 Razones trigonométricas – Ejercicio 5.3

Pregunta 1. Evalúa lo siguiente:

(i) sen 20°/cos 70°

Solución:

Dado: sen 20°/cos 70°

= sen(90° − 70°)/cos 70°

= cos 70°/cos 70° -(∵ sen (90° – θ) = cos θ)

= 1

Por lo tanto, sen 20°/cos 70° = 1

(ii) cos 19°/sen 71°

Solución:

Dado: cos 19°/sen 71°

= cos(90° − 71°)/sen 71°

= sen 71°/sen 71° -(∵ cos (90° – θ) = sen θ)

= 1

Por lo tanto, cos 19°/sen 71° = 1

(iii) sen 21°/cos 69°

Solución:

Dado: sen 21°/cos 69°

= sen(90° − 69°)/cos 69°

= cos 69°/cos 69° -(∵ sen (90° – θ) = cos θ)

= 1

Por lo tanto, sen 21°/cos 69° = 1

(iv) bronceado 10°/cuna 80°

Solución:

Dado: bronceado 10°/cuna 80°

= tan(90° − 80°)/cot 80°

= cuna 80°/cot 80° -(∵ tan (90° – θ) = cuna θ)

= 1

Por lo tanto, tan 10°/cot 80° = 1

(v) seg 11°/coseg 79°

Solución:

Dado: seg 11°/cosec 79°

= segundo(90° − 79°)/coseg 79°

= cosec 79°/cosec 79° -(∵ seg (90° – θ) = cosec θ)

= 1

Por lo tanto, seg 11°/cosec 79° = 1

Pregunta 2. Evalúa lo siguiente:

(yo) ( 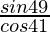$\frac{sin 49°}{cos 41°}$ ) ² + ( $\frac{cos 41°}{sin 49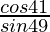°}$ ) ²

Solución:

Dado: ( $\frac{sin 49°}{cos 41°}$ ) ² + ( $\frac{cos 41°}{sin 49°}$ ) ²

= $(\frac{sin (90°-41°)}{cos 41°})^2+(\frac{cos 41°}{sin (90°-41°)})^2$ -(∵ sen (90° – θ) = cos θ)

= (cos 41°/cos 41°) ² + (cos 41°/cos 41°) ²

= 1 + 1 = 2

Por lo tanto, ( $\frac{sin 49°}{cos 41°}$ ) ² + ( $\frac{cos 41°}{sin 49°}$ ) ² = 2

(ii) cos 48° – sen 42°

Solución:

Dado: cos 48° – sen 42°

= cos 48° – sen (90°- 48°) -(∵ sen (90° – θ) = cos θ)

= cos 48° – cos 48°

= 0

Por lo tanto, cos 48° – sen 42° = 0

(iii) 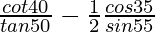$\frac{cot 40°}{tan 50°}-\frac{1}{2}\frac{cos 35°}{sin 55°}$

Solución:

Dado: $\frac{cot 40°}{tan 50°}-\frac{1}{2}\frac{cos 35°}{sin 55°}$

= $\frac{cot(90°-50°)}{tan 50°}-\frac{1}{2}(\frac{cos 35°}{sin (90°-35°)})$ -(∵ sin (90° – θ) = cos θ y cot (90° – θ) = tan θ)

= $\frac{tan 50°}{tan 50°}-\frac{1}{2}(\frac{cos 35°}{cos 35°})$

= 1 – 1/2 = 1/2

Por lo tanto, $\frac{cot 40°}{tan 50°}-\frac{1}{2}\frac{cos 35°}{sin 55°}$ = 1/2

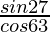(iv) ( $\frac{sin 27°}{cos 63°}$ ) ² – ( $\frac{cos 63°}{sin 27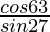°}$ ) ²

Solución:

Dado: ( $\frac{sin 27°}{cos 63°}$ ) ² – ( $\frac{cos 63°}{sin 27°}$ ) ²

= $(\frac{sin (90°-63°)}{cos 63°})^2-(\frac{cos 63°}{sin (90°-63°)})^2$ -(∵ sen (90° – θ) = cos θ)

= (cos 63°/cos 63°) ² – (cos 63°/cos 63°) ²

= 1 – 1 = 0

Por lo tanto, ( $\frac{sin 27°}{cos 63°}$ ) ² – ( $\frac{cos 63°}{sin 27°}$ ) ² = 0

(v) $\frac{tan 35°}{cot 55°}+\frac{cot 78°}{tan 12°}-1$

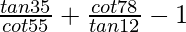
Solución:

Dado: $\frac{tan 35°}{cot 55°}+\frac{cot 78°}{tan 12°}-1$

= $\frac{tan (90°-55°)}{cot 55°}+\frac{cot 78°}{tan (90°-78°)}-1$ -(∵tan (90° – θ) = cuna θ)

=(cuna 55°/cuna 55°) + (cuna 78°/cuna 78°) – 1

= 1 + 1 – 1 = 1

Por lo tanto, $\frac{tan 35°}{cot 55°}+\frac{cot 78°}{tan 12°}-1$ = 1

(vi) $\frac{sec 70°}{cosec 20°}+\frac{sin 59°}{cos 31°}$

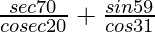
Solución:

Dado: $\frac{sec 70°}{cosec 20°}+\frac{sin 59°}{cos 31°}$

= $\frac{sec(90°−20°)}{cosec 20°}+\frac{sin(90°−31°)}{cos 31°}$ -(∵ seg (90° – θ) = cosec θ y sen (90° – θ) = cos θ)

= coseg 20°/coseg 20° + cos 31°/cos 31°

= 1 + 1 = 2

Por lo tanto, $\frac{sec 70°}{cosec 20°}+\frac{sin 59°}{cos 31°}$ = 2

(vii) cosec 31° – sec 59°

Solución:

Dado: cosec 31° – sec 59°

= cosec 31° – seg (90°- 31°) -(∵ seg (90° – θ) = cosec θ)

= cosec 31° – cosec 31°

= 0

Por lo tanto, cosec 31° – sec 59° = 0

(viii) (sen 72° + cos 18°)(sen 72° – cos 18°)

Solución:

Dado: (sen 72° + cos 18°)(sen 72° – cos 18°)

= (sen 72° + coseno (90° – 72°))(sen 72° – coseno (90° – 72°)) -(∵ sen (90° – θ) = cos θ)

= (sen 72° + sen 72°)(sen 72° – sen 72°)

= 0

Por lo tanto, (sen 72° + cos 18°)(sen 72° – cos 18°) = 0

(ix) sen 35° sen 55° – cos 35° cos 55°

Solución:

Dado: sen 35° sen 55° – cos 35° cos 55°

= (sen 35°sen (90°- 35°)) – (cos 35° cos (90° – 35°)) -(∵ sin (90° – θ) = cos θ y cos (90° – θ) = sen θ)

= (sen 35°cos 35°) – (cos 35° sen 35°)

= 0

Por lo tanto, sen 35° sen 55° – cos 35° cos 55° = 0

(x) bronceado 48° bronceado 23° bronceado 42° bronceado 67°

Solución:

Dado: bronceado 48° bronceado 23° bronceado 42° bronceado 67°

= tan 48° tan 23° tan (90° – 48°) tan (90° – 23°) -(∵ tan (90° – θ) = cot θ)

= bronceado 48° bronceado 23° cuna 48° cuna 23°

= 1

Por lo tanto, tan 48°tan 23°tan 42°tan 67° = 1

(xi) seg 50°sen 40° + cos 40°coseg 50°

Solución:

Dado: seg 50°sen 40° + cos 40°cosec 50°

= (seg 50°sen (90° – 50°)) + (cos 40° cosec(90° – 40°)) -(∵ sen (90° – θ) = cos θ y coseg (90° – θ) = segundo θ)

= (seg 50°cos 50°) + (cos 40° seg 40°)

= 1 + 1 = 2

Por lo tanto, sec 50°sen 40° + cos 40°cosec 50° = 2

Pregunta 3. Exprese cada uno de los siguientes en términos de razones trigonométricas de ángulos que se encuentran entre 0° y 45°

(i) sen 59° + cos 56°

Solución:

Dado: sen 59° + cos 56°

= sen (90° – 31°) + coseno (90° – 34°)

= cos 31° + sen 34°

(ii) bronceado 65° + cuna 49°

Solución:

Dado: bronceado 65° + cuna 49°

= bronceado (90° – 25°) + cuna (90° – 31°)

= cuna 25° + bronceado 31°

(iii) seg 76° + cosec 52°

Solución:

Dado: sec 76° + cosec 52°

= segundo (90° – 14°) + cosegundo (90° – 38°)

= cosec 14° + sec 38°

(iv) cos 78° + seg 78°

Solución:

Dado: cos 78° + seg 78°

= coseno (90° – 12°) + segundo (90° – 12°)

= sen 12° + cosec 12°

(v) cosec 54° + sen 72°

Solución:

Dado: cosec 54° + sin 72°

= cosec (90° – 36°) + sin (90° – 18°)

= seg 36° + cos 18°

(vi) cuna 85° + cos 75°

Solución:

Dado: cot 85° + cos 75°

= cuna (90° – 5°) + coseno (90° – 15°)

= bronceado 5° + pecado 15°

(vii) sen 67° + cos 75°

Solución:

Dado: sen 67° + cos 75°

= seno (90° – 23°) + coseno (90° – 15°)

= cos 23° + sen 15°

Pregunta 4. Exprese cos 75° + cot 75° en términos de ángulos que se encuentran entre 0° y 30°.

Solución:

Dado: cos 75° + cot 75°

= coseno (90° – 15°) + cuna (90° – 15°)

= sen 15° + tan 15°

Pregunta 5. Si sen 3A = cos(A – 26°), donde 3A es un ángulo agudo, encuentra el valor de A.

Solución:

Dado: sen 3A = cos(A – 26°)

= coseno (90° – 3A) = coseno(A – 26°)

Ahora, 90° – 3A = A – 26°

= A + 3A = 90° + 26°

= 4A = 116°

= A = 29°

Por lo tanto, el valor de A es 29°

Pregunta 6. Si A, B, C son los ángulos interiores de un triángulo ABC, prueba que

(i) bronceado (C+ A)/2 = cuna B/2

Solución:

Según la pregunta

En el triángulo ABC, A, B, C son los ángulos interiores

Asi que,

A + B + C = 180°

C+ A = 180° – B

Tomando LHS

bronceado (C+ A)/2 = bronceado (180° – B)/2

= tan (90° – B)/2 -(∵ tan (90° – θ) = cot θ)

= cuna B/2 = RHS

LHS = RHS

Por lo tanto probado

(ii) sen (B + C)/2 = cos A/2

Solución:

Según la pregunta

En el triángulo ABC, A, B, C son los ángulos interiores

Asi que,

A + B + C = 180°

B + C = 180° – A

Tomando LHS

= sen (B + C)/2 = sen (180° – A)/2

= sen (90° – A/2) -(∵ sen (90° – θ) = cos θ)

= cos A/2

LHS = RHS

Por lo tanto probado

Pregunta 7. Demuestra que:

(i) tan20°tan35°tan45°tan55°tan70° = 1

Solución:

Tenemos que probar que tan20°tan35°tan45°tan55°tan70° = 1

Tomando LHS

= tan20°tan35°tan45°tan55°tan70°

= tan(90° − 70°)tan(90° − 55°)tan45°tan55°tan70° -(∵ tan (90° – θ) = cot θ)

= cot70°cot55°tan45°tan55°tan70°

= (1/tan70°)(1/tan55°)tan45°tan55°tan70° (∵ cot θ = 1/tan θ)

= tan45°

= 1

LHS = RHS

Por lo tanto probado

(ii) sen48°sec42° + cos48°cosec42° = 2

Solución:

Tenemos que probar que sen48°sec42° + cos48°cosec42° = 2

Tomando LHS

= sen48°sec42° + cos48°cosec42° (∵ seg θ = 1/cos θ y cosec θ = 1/sen θ)

= $\frac{sin48°}{cos(90°−48°)} + \frac{cos48°}{sin(90°−48°)}$ -(∵ sen (90° – θ) = cos θ y cos (90° – θ) = sen θ)

= sin48°/sin48° + cos48°/cos48°

= 1 + 1

= 2

LHS = RHS

Por lo tanto probado

(iii) 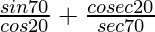$\frac{sin 70°}{cos 20°}+\frac{cosec 20°}{sec 70°}$ – 2cos70° cosec20° = 0

Solución:

Tenemos que probar que $\frac{sin 70°}{cos 20°}+\frac{cosec 20°}{sec 70°}$ – 2cos70° cosec20° = 0

Tomando LHS

= sen 70°/cos 20° + coseg 20°/seg 70° – 2cos70° coseg20°

= $\frac{sin 70°}{cos (90°-70°)} + \frac{cosec 20°}{sec(90°-20°)} - 2cos 70°cosec (90°-70°)$

= sen 70°/sen 70° + coseg 20°/coseg 20° – 2cos 70°seg 70°

= 1 + 1 – 2cos 70°/cos 70°

= 0

LHS = RHS

Por lo tanto probado

(iv) 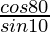$\frac{cos 80°}{sin 10°}$ + cos 59° cosec31° = 2

Solución:

Tenemos que demostrar que $\frac{cos 80°}{sin 10°}$ + cos 59°cosec31° = 2

Tomando LHS

= cos 80°/sen 10° + cos 59° cos 31°

= coseno 80°/sen (90° – 80°) + coseno 59°coseg(90°-59°)

= cos 80°/cos 80° + cos 59°/cos 59°

= 1 + 1 = 2

LHS = RHS

Por lo tanto probado

Publicación traducida automáticamente

Artículo escrito por rahulsharma1771996 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 10 Soluciones RD Sharma – Capítulo 5 Razones trigonométricas – Ejercicio 5.3 | Serie 1

Pregunta 1. Evalúa lo siguiente:

(i) sen 20°/cos 70°

(ii) cos 19°/sen 71°

(iii) sen 21°/cos 69°

(iv) bronceado 10°/cuna 80°

(v) seg 11°/coseg 79°

Pregunta 2. Evalúa lo siguiente:

(yo) ( $\frac{sin 49°}{cos 41°}$ ) ² + ( $\frac{cos 41°}{sin 49°}$ ) ²

(ii) cos 48° – sen 42°

(iii) $\frac{cot 40°}{tan 50°}-\frac{1}{2}\frac{cos 35°}{sin 55°}$

(iv) ( $\frac{sin 27°}{cos 63°}$ ) ² – ( $\frac{cos 63°}{sin 27°}$ ) ²

(v) $\frac{tan 35°}{cot 55°}+\frac{cot 78°}{tan 12°}-1$

(vi) $\frac{sec 70°}{cosec 20°}+\frac{sin 59°}{cos 31°}$

(vii) cosec 31° – sec 59°

(viii) (sen 72° + cos 18°)(sen 72° – cos 18°)

(ix) sen 35° sen 55° – cos 35° cos 55°

(x) bronceado 48° bronceado 23° bronceado 42° bronceado 67°

(xi) seg 50°sen 40° + cos 40°coseg 50°

Pregunta 3. Exprese cada uno de los siguientes en términos de razones trigonométricas de ángulos que se encuentran entre 0° y 45°

(i) sen 59° + cos 56°

(ii) bronceado 65° + cuna 49°

(iii) seg 76° + cosec 52°

(iv) cos 78° + seg 78°

(v) cosec 54° + sen 72°

(vi) cuna 85° + cos 75°

(vii) sen 67° + cos 75°

Pregunta 4. Exprese cos 75° + cot 75° en términos de ángulos que se encuentran entre 0° y 30°.

Pregunta 5. Si sen 3A = cos(A – 26°), donde 3A es un ángulo agudo, encuentra el valor de A.

Pregunta 6. Si A, B, C son los ángulos interiores de un triángulo ABC, prueba que

(i) bronceado (C+ A)/2 = cuna B/2

(ii) sen (B + C)/2 = cos A/2

Pregunta 7. Demuestra que:

(i) tan20°tan35°tan45°tan55°tan70° = 1

(ii) sen48°sec42° + cos48°cosec42° = 2

(iii) $\frac{sin 70°}{cos 20°}+\frac{cosec 20°}{sec 70°}$ – 2cos70° cosec20° = 0

(iv) $\frac{cos 80°}{sin 10°}$ + cos 59° cosec31° = 2

Deja una respuesta Cancelar la respuesta

Pregunta 1. Evalúa lo siguiente:

(i) sen 20°/cos 70°

(ii) cos 19°/sen 71°

(iii) sen 21°/cos 69°

(iv) bronceado 10°/cuna 80°

(v) seg 11°/coseg 79°

Pregunta 2. Evalúa lo siguiente:

(yo) ( ) 2 + ( ) 2

(ii) cos 48° – sen 42°

(iii)

(iv) ( ) 2 – ( ) 2

(v)

(vi)

(vii) cosec 31° – sec 59°

(viii) (sen 72° + cos 18°)(sen 72° – cos 18°)

(ix) sen 35° sen 55° – cos 35° cos 55°

(x) bronceado 48° bronceado 23° bronceado 42° bronceado 67°

(xi) seg 50°sen 40° + cos 40°coseg 50°

Pregunta 3. Exprese cada uno de los siguientes en términos de razones trigonométricas de ángulos que se encuentran entre 0° y 45°

(i) sen 59° + cos 56°

(ii) bronceado 65° + cuna 49°

(iii) seg 76° + cosec 52°

(iv) cos 78° + seg 78°

(v) cosec 54° + sen 72°

(vi) cuna 85° + cos 75°

(vii) sen 67° + cos 75°

Pregunta 4. Exprese cos 75° + cot 75° en términos de ángulos que se encuentran entre 0° y 30°.

Pregunta 5. Si sen 3A = cos(A – 26°), donde 3A es un ángulo agudo, encuentra el valor de A.

Pregunta 6. Si A, B, C son los ángulos interiores de un triángulo ABC, prueba que

(i) bronceado (C+ A)/2 = cuna B/2

(ii) sen (B + C)/2 = cos A/2

Pregunta 7. Demuestra que:

(i) tan20°tan35°tan45°tan55°tan70° = 1

(ii) sen48°sec42° + cos48°cosec42° = 2

(iii) – 2cos70° cosec20° = 0

(iv) + cos 59° cosec31° = 2

Deja una respuesta Cancelar la respuesta

(yo) ( $\frac{sin 49°}{cos 41°}$ ) ² + ( $\frac{cos 41°}{sin 49°}$ ) ²

(iii) $\frac{cot 40°}{tan 50°}-\frac{1}{2}\frac{cos 35°}{sin 55°}$

(iv) ( $\frac{sin 27°}{cos 63°}$ ) ² – ( $\frac{cos 63°}{sin 27°}$ ) ²

(v) $\frac{tan 35°}{cot 55°}+\frac{cot 78°}{tan 12°}-1$

(vi) $\frac{sec 70°}{cosec 20°}+\frac{sin 59°}{cos 31°}$

(iii) $\frac{sin 70°}{cos 20°}+\frac{cosec 20°}{sec 70°}$ – 2cos70° cosec20° = 0

(iv) $\frac{cos 80°}{sin 10°}$ + cos 59° cosec31° = 2