Pregunta 1. Determinar la naturaleza de las raíces de las siguientes ecuaciones cuadráticas:
(yo) 2x² – 3x + 5 = 0
(ii) 2x² – 6x + 3 = 0
(iii) 3/5 x² – 2/3 x + 1 = 0
(iv) 3x² – 4√3x + 4 = 0
(v) 3x² – 2√6x + 2 = 0
Solución:
(yo) 2x² – 3x + 5 = 0
Aquí a=2, b=-3, c=5
D=b 2 -4ac=(-3) 2 -4*2*5
=-9-40=-31
D<0
Las raíces no son reales.
(ii) 2x² – 6x + 3 = 0
Aquí a=2, b=-6, c=3
D=b 2 -4ac
=(-6) 2 -4*2*3=36-24=12
D>0
Las raíces son reales y distintas.
(iii) 3/5 x² – 2/3 x + 1 = 0
Aquí a=3/5, b=-2/3, c=1
Discriminante (D)=b 2 -4ac
D<0
Las raíces no son reales.
(iv) 3x² – 4√3x + 4 = 0
Aquí a=3, b=-4√3, c=4
D=b 2 -4ac
=(-4√3)2-4*3*4=48-48=0
D=0
Las raíces son reales e iguales.
(v) 3x² – 2√6x + 2 = 0
Aquí a=3, b=– 2√6, c=2
Discriminante (D)=b 2 -4ac
=(– 2√6)2-4*3*2=24-24=0
D=0
Las raíces son reales e iguales.
Pregunta 2. Encuentra los valores de k para los cuales las raíces son reales e iguales en cada una de las siguientes ecuaciones:
(i) kx² + 4x + 1 = 0
Solución:
Aquí a=k, b=4, c=1
Discriminante(D)=b2-4ac
=(4) 2 -4*k*1
=16-4k
Las raíces son reales e iguales.
D=0
16-4k=0⇒4k=16
k=16/4=4
Por lo tanto k=4
(ii) kx² – 2√5 x + 4 = 0
Solución:
Aquí a=k, b=-2√5, c=4
Discriminante(D)=b 2 -4ac
=( – 2√5 )-4*k*4=20-16k
Las raíces son reales e iguales.
D=0
20-16k=0⇒ 16k=20
k=20/16=5/4
Por lo tanto k=5/4
(iii) 3x² – 5x + 2k = 0
Solución:
Aquí a=3, b=-5, c=2k
Discriminante (D)=b 2 -4ac
=(-5) 2 -4*3*2k
=25-24k
Las raíces son reales e iguales.
D=0
25-24k=0⇒24k=25
k=25/24
(iv) 4x²+ kx + 9 = 0
Solución:
Aquí a=4, b=k, c=9
Discriminante (D)=b 2 -4ac
=k 2 -4*4*9=k2-144
Las raíces son reales e iguales.
k2 -144= 0⇒k2 = 144=(±12) 2
(v) 2kx² – 40x + 25 = 0
Solución:
Aquí a=2k, b=-40, c=25
Discriminante(D)=b 2 -4ac
=(-40) 2 -4*2k*25
=1600-200k
Las raíces son reales e iguales.
D=0
1600-200k=0⇒200k=1600
k=1600/200=8
Por lo tanto k=8
(vi) 9x² – 24x + k = 0
Solución:
Aquí a=9, b=-24, c=k
Discriminante(D)=b 2 -4ac
=(-24) 2 -4*9*k
=576-36k
Las raíces son reales e iguales.
D=0
576-36k=0
36k=576⇒k=576/36=16
k=16
(vii) 4x² – 3kx +1 = 0
Solución:
Aquí a=4, b=-3k, c=1
Discriminante (D)=b 2 -4ac
=(-3k) 2 -4*4*1
=9k2-16
Las raíces son reales e iguales.
D=0
9k 2 -16=0⇒9k2=16
k2 = 16/9=
(viii) x² – 2 (5 + 2k) x + 3 (7 + 10k) = 0
Solución:
Aquí a=1, b=-2(5+2k) y c=3(7+10k)
Discriminante (D)=b 2 -4ac
[-2(5+2k)] 2 -4*1*3(7+10k)
=4(25+4k 2 +20k)-12(7+10k)
=100+16k 2 +80k-84-120k
16k 2 -40k+16
Las raíces son reales e iguales.
D=0
16k 2 -40k+16=0
2k 2 -5k+2=0
2k 2 -4k-k+2=0
2k(k-2)-1(k-2)=0
(k-2)(2k-1)=0
Ya sea k-2=0, luego k=2 o 2k-1=0, luego 2k=1⇒k=1/2
Por lo tanto, k=2, 1/2
(ix) (3k + 1) x² + 2(k + 1) x + k = 0
Solución:
Aquí a=3k+1, b=2(k+1), c=k
Discriminante(D)=b 2 -4ac
=[2(k+1)] 2 -4*(3k+1)*k
=4(k 2 +2k+1)-4k(3k+1)
=4k 2 +8k+4-12k2-4k
-8k 2 +4k+4
Las raíces son reales e iguales.
D=0
-8k 2 +4k+4=0
2k 2 -k-1=0 (Dividiendo por -4)
2k 2 -2k+k-1= {Por lo tanto -2=-2*1
-1=-2+1}
2k(k-1)+1(k-1)=0
(k-1)(2k+1)=0
Ya sea k-1=0, luego k=1 o 2k+1=0, luego 2k=-1⇒k=-1/2
k=1,-1/2
(x) kx² + kx + 1 = – 4x² – x
Solución:
kx² +4x 2 +kx+x+1=0
(k+4)x 2 +(k+1)x+1=0
Aquí a=k+4, b=k+1, c=1
Discriminante(D)=b 2 -4ac
=(k+1) 2 -4*(k+4)*1
=k 2 +2k+1-4k-16
=k 2 -2k-15
Las raíces son reales e iguales.
D=0
k2-2k – 15 =0
k 2 -5k+3k-15=0 {Por lo tanto -15=-5*3
-2=-5+3}
k(k-5)+3(k-5)=0
(k-5)(k+3)=0
Ya sea k-5=0, entonces k=5
o k+3=0, entonces k=-3
Por lo tanto k=5,-3
(xi) (k + 1) x² + 2 (k + 3) x + (k + 8) = 0
Solución:
Aquí a=k+1, b=2(k+3), c=k+8
Discriminante(D)=b 2 -4ac
=[2(k+3)] 2 -4(k+1)(k+8)
=4(k 2 +6k+9)-4)(k2+9k+8)
=4k 2 +24k+36-4k 2 -36k-32
=-12k+4
Las raíces son reales e iguales.
D=0
-12k+4=0
12k=4⇒k=4/12=1/3
Por lo tanto k=1/3
(xii) x² – 2kx + 7k – 12 = 0
Solución:
Aquí a=1, b=-2k, c=(7k-12)
Discriminante(D)=b 2 -4ac
=(-2k) 2 -4*1*(7k-12)
=4k 2 -4(7k-12)
=4k 2 -28k+48
Las raíces son reales e iguales.
D=0
4k 2 -28k+48=0
k 2 -7k+12=0 (Dividiendo por 4 )
k2-3k -4k+12=0 {12=-3*(-4 )
-7=-3-4}
k(k-3)-4(k-3)=0
(k-3)(k-4)=0
O bien, k-3=0, entonces k=3
o k-4=0, entonces k=4
Por lo tanto, k=3,4
(xiii) (k + 1) x² – 2 (3k + 1) x + 8k + 1 = 0
Solución:
Aquí a=k+1, b=-2(3k+1), c=8k+1
Discriminante(D)=b 2 -4ac
=[-2(3k+1) 2 -4*(k+1)(8k+1)]
=4(9k 2 +6k+1)-4(8k2+9k+1)
=36k 2 +24k+4-32k 2 -36-4
=4k 2 -12k
Las raíces son reales e iguales.
D=0
4k 2 -12k=0
k 2 -3k=0 ————–(Dividiendo por 4)
k(k-3)=0
Ya sea k=0
o k-3=0, entonces k=3
k=3,0
(xiv) 5x² – 4x + 2 + k (4x² – 2x – 1) = 0
Solución:
5x 2 -4x+2+4kx2-2kx-k=0
(5+4k)x 2 -(4+2k)x+(2-k)=0
Aquí a=5+4k, b=-(4+2k), c=2-k
Discriminante (D)=b 2 -4ac
=[-(4+2k)] 2 -4*(5+4k)(2-k)
=16+4k 2 +16k-4(10-5k+8k-4k 2 )
=16+4k 2 +16k-40+20k-32k+16k 2
=20k 2 +4k-24
Las raíces son reales e iguales.
D=0
20k 2 +4k-24=0
5k 2 +k-6=0 —–(Dividiendo por 4)
5k 2 +6k-5k-6=0
k(5k+6)-1(5k+6)=0
(5k+6)(k-1)=0
5k+6=0, luego 5k=-6⇒k=-6/5
o k-1=0, entonces k=1
k=1,
(xv) (4 – k) x² + (2k + 4) x (8k + 1) = 0
Solución:
Aquí a=4-k, b=2k+4, c=8k+1
Discriminante (D)=b 2 -4ac
=(2k+4) 2 -4*(4-k)(8k+1)
=4k 2 +16k+16-4(32k+4-8k 2 -k)
=4k 2 +16k+16-128k-16+32k 2 +4k
=36k 2 -108k
Las raíces son reales e iguales.
36k 2 -108k=0
k2-3k = 0⇒k(k-3)=0
Ya sea k=0
o k-3=0, entonces k=3
Por lo tanto k=0,3
(xvi) (2k + 1) x² + 2 (k + 3) x (k + 5) = 0
Solución:
Aquí a=2k+1, b=2(k+3), c=k+5
Discriminante (D)=b 2 -4ac
=[2(k+3)] 2 -4(2k+1)(k+5)
=4(k 2 +6k+9)-4(2k 2 +10k+k+5)
=4k 2 +24k+36-8k 2 -40k-4k-20
=-4k 2 -20k+16
Las raíces son reales e iguales D=0
-4k 2 -20k+16=0
k 2 +5k-4=0 ———-(Dividiendo por -4)
Aquí a=1, b=5, c=-4
Discriminante (D)=b 2 -4ac
=(5) 2 -4*1*(-4)=25+16=41
(xvii) 4x² – 2 (k + 1) x + (k + 4) = 0
Solución:
Aquí a=4, b=-2(k+1), c=k+4
Discriminante (D)=b 2 -4ac
=[-2(k+1)] 2 -4*4*(k+4)
=4(k 2 +2k+1)-16(k+4)
=4k 2 +8k+4-16k-64
=4k 2 -8k-12
Las raíces son reales e iguales.
D=0
4k 2 -8k-60=0
k 2 -2k-15=0 ————-(Dividiendo por 4)
k 2 -5k+3k-15=0
k(k-5)+3(k-5)=0
(k-5)(k+3)=0
Ya sea k-5=0, entonces k=5
o k+3=0, entonces k=-3
k=5,-3
(xviii) 4x² (k + 1) x + (k + 1) = 0
Solución:
Aquí a=4, b=-2(k+1), c=k+1
Discriminante (D)=b 2 -4ac
=[-2(k+1)] 2 -4*4*(k+1)
=4(k 2 +2k+1)-16(k+1)
=4k 2 +8k+4-16k-16
=4k 2 -8k-12
k 2 -2k-3=0 ————(Dividiendo por 4)
k2-3k2 + k – 3 =0
k(k-3)+(k-3)=0
(k-3)(k+1)=0
O bien (k-3)=0, entonces k=3
o (k+1)=0, entonces k=-1
k=-1,3
Pregunta 3. A continuación, determine el conjunto de valores de k para los cuales la ecuación cuadrática dada tiene raíces reales:
(yo) 2x² + 3x + k = 0
Solución:
Aquí a=2, b=3, c=k
Discriminante (D)=b 2 -4ac
=(3) 2 -4*2*k
=9-8k
Las raíces son reales
D≥0
9-8k≥0⇒9≥8k⇒8k≤9
k≤9/8
(ii) 2x² + x + k = 0
Solución:
Aquí a=2, b=1, c=k
Discriminante (D)=b 2 -4ac
=(1) 2 -4*2*k
=1-8k
Las raíces son reales
D≥0
1-8k≥0⇒1≥8k
8k≤1
k≤1/8
(iii) 2x² – 5x – k = 0
Solución:
Discriminante (D)=b 2 -4ac
=(-5) 2 -4*2*(-k)
=25+8k
Las raíces son reales
D≥0
25+8k≥0
8k≥-25⇒≥-25/8
k≥-25/8
(iv) kx² + 6x + 1 = 0
Solución:
Discriminante (D)=b 2 -4ac
=(6) 2 -4*k*1
=36-4k
Las raíces son reales
D≥0⇒36-4k≥0
36≥4k⇒4k≤36
k≤36/4⇒k≤9
k≤9
(v) 3x² + 2x + k = 0
Solución:
Aquí a=3, b=2, c=k
Discriminante (D)=b 2 -4ac
=(2)2-4*3*k=4-12k
Las raíces son reales
D≥0⇒4-12k≥0
4≥12k⇒12k≤0
4≥12k⇒12k≤4
k≤
⇒k≤1/3
Pregunta 4. Encuentra los valores de k para los cuales las siguientes ecuaciones tienen raíces reales e iguales:
(i) x²- 2(k + 1) x + k² = 0
Solución:
Aquí a=1, b=2(k+1), c=k 2
Discriminante (D)=b 2 -4ac
=[2(k+1)] 2 -4*1*k 2
=4(k 2 +2k+1)-4k 2
=4k 2 +8k+4-k 2
=8k+4
Las raíces son reales e iguales.
D=0
8k+4=0⇒8k=-4
k=-4/8=-1/2, por lo tanto k=-1/2
(ii) k²x² – 2 (2k – 1) x + 4 = 0
Solución:
Aquí, a=k2, b=-2(2k-1), c=4
Discriminante (D)=b 2 -4ac
=[-2(2k-1)] 2 -4*k 2 *4
=4(4k 2 -4k+1)-16k 2
= 16k2 -16k + 4-16k2 = -16k+4
Las raíces son reales e iguales.
D=0
-16k+4=0⇒-16k=-4
k=4/16=1/4
k=1/4
(iii) (k + 1) x² – 2(k – 1) x + 1 = 0
Solución:
Aquí, a=k+1, b=-2(k-1) y c=1
Discriminante (D)=b 2 -4ac
=[-2(k-1)] 2 -4(k+1)*1
=4(k 2 -2k+1)-4(k+1)
=4k 2 -8k+4-4k-4=4k 2 -12k
Las raíces son reales e iguales.
D=0
4k2-12k=0
k2-3k=0 ————-(Dividiendo por 4)
Ya sea k=0
o k-3=0, entonces k=3
k=0,3
(iv) x² + k(2x + k – 1) + 2 = 0
Solución:
Aquí, a=1, b=2k, c=(k 2 -k+2)
Discriminante (D)=b 2 -4ac
=(2k) 2 -4*1*(k 2 -k+2)
=4k 2 -4k 2 +4k-8
=4k-8
Las raíces son reales e iguales.
D=0
4k-8=0⇒k=2
Por lo tanto, k=2
Pregunta 5. Encuentra los valores de k para los cuales las siguientes ecuaciones tienen raíces reales
(yo) 2x² + kx + 3 = 0
Solución:
Aquí a = 2, b = k, c = 3
Las raíces son reales e iguales.
D=0
k2 -24 = 0⇒k2 = 24
k=±√24=±√4*6=±2√6
(ii) kx (x – 2) + 6 = 0
Solución:
kx 2 -2kx+6=0
aquí, a=k, b=-2k, c=6
Discriminante (D)=b 2 -4ac=(-2k) 2 -4*k*6=4k 2 -24k
Las raíces son reales e iguales.
D=0
4k 2 -24k=0⇒4k(k-6)=0
k(k-6)=0
Ya sea k = 0 o
k-6=0, entonces k=6
k=0,6
(iii) x² – 4kx + k = 0
Solución:
Aquí, comparando con ax 2 +kx+c=0
a=1, b=-4k, c=k
Discriminante (D)=b 2 -4ac=(-4k)2-4*1*k=16k2-4k
Las raíces son reales e iguales.
D=0
16k 2 -4k=0⇒4k(4k-1)=0
k(4k-1)=0
Ya sea k=0
o 4k-1=0⇒4k=1
k=1/4, por lo tanto k=0,1/4
(iv) kx(x – 2√5) + 10 = 0
Solución:
Aquí a=k, b=-2√5k, c=10
D=b 2 -4ac
=(-2√5k) 2 -4(k)(10)=20k 2 -40k
Las raíces son iguales D=0
20k 2 -40k=0
k-2=0 ———(Dividiendo por 20k)
k=2
(v) kx (x – 3) + 9 = 0
Solución:
Aquí, a=k, b=-3k, c=9
D=b 2 -4ac
=(-3k) 2 -4(k)9
=9k 2 -36k
Para que las raíces sean reales
D=0
9k 2 -36k=0
9k(k-4)=0
k-4=0⇒k=4
k=4
(vi) 4x² + kx + 3 = 0
Solución:
Aquí, a=4, b=k, c=3
D=b 2 -4ac
=k2-4(4)(3)
=k2-48
Para que las raíces sean reales
D=0
k2-48=0
k2=48
k=±√48=±
k=±
Pregunta 6. Encuentra los valores de k para los cuales la ecuación cuadrática dada tiene raíces reales y distintas:
(i) kx² + 2x + 1 = 0
Solución:
Aquí, a=k, b=2, c=1
D=b 2 -4ac
=(2) 2 -4*k*1
=4-4k
Las raíces son reales y distintas.
D>0⇒4-4k>0
1-k>0⇒1>k
⇒k<1
Por lo tanto, k<1
(ii) kx² + 6x + 1 = 0
Solución:
Aquí, a=k, b=6, c=1
D=b 2 -4ac
=(6)2-4*k*1
=36-4k
Las raíces son reales y distintas.
D>0⇒36-4k>0
9-k>0⇒9>k
⇒k<9
Por lo tanto, k<9
Pregunta 7. Para qué valor de k, (4 – k) x² + (2k + 4) x + (8k + 1) = 0, es un cuadrado perfecto.
Solución:
(4 – k) x² + (2k + 4) x + (8k + 1) = 0
Aquí, a = 4 – k, b = 2k + 4, c = 8k + 1
=(2k+4) 2 -4*(4-k)(8k+1)
=4k 2 +16k+16-4(32k+4-8k 2 -k)
=4k 2 +16k+16-4(-8k 2 +31k+4)
=4k 2 +16k+16+32k 2 -124k-16
=36k 2 -108k
Por lo tanto, la ecuación cuadrática dada es un cuadrado perfecto
Las raíces son reales e iguales.
D=0⇒36k 2 -108k=0
Ya sea k=0
o k-3=0⇒k=3
k=0,3
Pregunta 8. Encuentra el valor mínimo positivo de k para el cual la ecuación x² + kx + 4 = 0 tiene raíces reales.
Solución:
x² + kx + 4 = 0
Aquí, a=1, b=k, c=4
Por lo tanto, Discriminante(D)=b 2 -4ac
=(k) 2 =4*1*4
= k 2 -16
tiene raíces reales
D≥0⇒k 2 -16≥0
⇒k2≥16⇒(k) 2 ≥(±4) 2
k≥4 o k≤-4
Valor mínimo positivo de k=4
Pregunta 9. Encuentra el valor de k para el cual la ecuación cuadrática (3k + 1) x² + 2(k + 1) x + 1 = 0 tiene raíces iguales. Además, encuentra las raíces.
Solución:
(3k + 1) x² + 2(k + 1) x + 1 = 0
Aquí a=(3k+1), b=2(k+1),c=1
Ahora, b 2 -4ac=[2(k+1)] 2 -4*(3k+1)*1
=4(k 2 +2k+1)-4(3k+1)
=4k 2 +8k+4-12k-4
=4k 2 -4k
Las raíces son reales e iguales.
b 2 -4ac=0
4k 2 -4k=0
k2- k = 0 k(k-1)=0
Ya sea k=0 o k-1=0, entonces k=1
k=0,1
(i) Cuando k=0, entonces
(3*0*1)x2 + 2 (0+1)x+1=0
x2 + 2x +1=0
(x+1) 2 =0
x+1=0
x=-1
Cuando k=1, entonces
(3*1+1)x2 + 2 (1+1)x+1=0
4×2 + 4×2 + 1 =0
(2x+1) 2 =0
2x+1=0
2x=-1⇒x=-1/2
x=1, -1/2
Pregunta 10. Encuentra los valores de p para los cuales la ecuación cuadrática (2p + 1) x² – (7p + 2) x + (7p – 3) = 0 tiene raíces iguales. Además, encuentre estas raíces.
Solución:
Aquí, a=2-+1, b=-(7p+2), c=(7p-3)
D=0 [Raíces iguales]
Como b 2 -4ac=0
[-(7p+)] 2 -4(2p+1)(7p-3)=0
(7p+2) 2 -4(14p 2 -6p+7p-3)=0
49p 2 +28p+4-56p 2 +24p-28p+12=0
-7p 2 +24p+16=0
7p 2 -24-16=0 ————-(Dividiendo ambos lados por -1)
7p(p-4)+4(p-4)=0
(p-4)(7p+4)=0
p-4=0 o 7p+4=0
p=4 o p=-4/7
Las raíces son x=-b/2a [Como raíces iguales (dado)]
Donde p=4,
raíces iguales es 5/3
Cuando p=-4/7
raíces iguales son 5/3 y 7
Publicación traducida automáticamente
Artículo escrito por ysachin2314 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
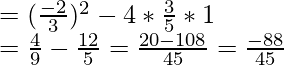
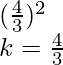
![Rendered by QuickLaTeX.com x=\frac{[7(\frac{-4}{7})+2]}{[2(\frac{-4}{7}+1)]}\\ =\frac{\frac{(-28+14)}{7}}{2\frac{-8+7}{7}}=\frac{-14}{-2}=7](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2ddf41ae66e2d19f30d3b38e5d335802_l3.png)