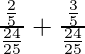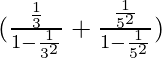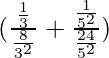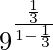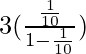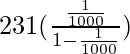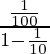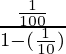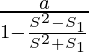Clase 11 RD Sharma – Capítulo 20 Progresiones Geométricas- Ejercicio 20.4

Pregunta 1.1 Encuentra la suma de las siguientes series hasta el infinito: 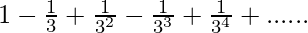$1-\frac13+\frac1{3^2}-\frac1{3^3}+\frac1{3^4}+......∞$

Solución:

serie dada: $1-\frac13+\frac1{3^2}-\frac1{3^3}+\frac1{3^4}+......∞$

Está en forma de progresión geométrica donde el primer término = 1 y la razón común = -1/3

Sabemos que la suma de los términos de GP hasta el infinito es S= $\frac{a}{1-r}$ donde a=primer término y r=razón común

Así, al sustituir el valor de a y r en esa fórmula

S= $\frac1{1-{(-\frac13)}}$

= $\frac1{1+\frac13}$

=3/4

De este modo, $1-\frac13+\frac1{3^2}-\frac1{3^3}+\frac1{3^4}+......∞=3/4$

Pregunta 1.2 Encuentra la suma de las siguientes series hasta el infinito: 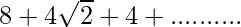$8+4\sqrt2+4+..........∞$

Solución :

serie dada $8+4\sqrt2+4+..........∞$

Está en forma de progresión geométrica donde el primer término = 8 y la razón común = 1/√2

Sabemos que la suma de los términos de GP hasta el infinito es S= $\frac{a}{1-r}$

donde a=primer término y r=razón común

Así, al sustituir el valor de a y r en esa fórmula

S= $\frac8{1-{\frac1{\sqrt2}}}$

= $\frac{8\sqrt2}{\sqrt2-1}$

= 8√2(√2+1)

=16+8√2

Por lo tanto, $8+4\sqrt2+4+..........∞$ =16+8√2

Pregunta 1.3 Encuentra la suma de las siguientes series hasta el infinito: $\frac25+\frac3{5^2}+\frac2{5^3}+\frac3{5^4}+.......∞$

Solución:

serie dada $\frac25+\frac3{5^2}+\frac2{5^3}+\frac3{5^4}+.......∞$

⇒ $(\frac25+\frac2{5^3}+......∞)+(\frac3{5^2}+\frac3{5^4}+.....∞)$

Estas dos ecuaciones están en forma de progresión geométrica.

Sabemos que la suma de los términos de GP hasta el infinito es S= $\frac{a}{1-r}$

donde a=primer término y r=razón común

Así, al sustituir el valor de a y r en esa fórmula

S= $(\frac{\frac25}{1-\frac1{25}}+\frac{\frac35}{1-\frac1{25}})$

= $\frac{\frac25}{\frac{24}{25}}+\frac{\frac35}{\frac{24}{25}}$

= $\frac1{\frac{24}{25}}$

=25⁄24

De este modo, $\frac25+\frac3{5^2}+\frac2{5^3}+\frac3{5^4}+.......∞=\frac{25}{24}$

Pregunta 1.4 Encuentra la suma de las siguientes series hasta el infinito: 10-9+8.1-7.29+……….∞

Solución:

Serie dada: 10-9+8.1-7.29+……….∞

⇒ $10-9+\frac{81}{10}-\frac{729}{100}+........ ∞$

Las series anteriores están en Progresión Geométrica con primer término=10 y razón común=-9⁄10

Sabemos que la suma de los términos de GP hasta el infinito es S= $\frac{a}{1-r}$

donde a=primer término y r=razón común

Así, al sustituir el valor de a y r en esa fórmula

⇒ S= $\frac{10}{1-(-\frac{9}{10})}$

⇒ S=100⁄19

De este modo $10-9+8.1-7.29+..........∞=\frac{100}{19}$

Pregunta 1.5 Encuentra la suma de las siguientes series hasta el infinito: 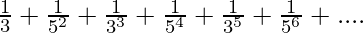$\frac13+\frac1{5^2}+\frac1{3^3}+\frac1{5^4}+\frac1{3^5}+\frac1{5^6}+....∞$

Solución:

serie dada: $\frac13+\frac1{5^2}+\frac1{3^3}+\frac1{5^4}+\frac1{3^5}+\frac1{5^6}+....∞$

⇒ $(\frac13+\frac1{3^3}+\frac1{3^5}+....∞)+(\frac1{5^2}+\frac1{5^4}+....∞)$

Estas dos ecuaciones están en forma de progresión geométrica.

Sabemos que la suma de los términos de GP hasta el infinito es S= $\frac{a}{1-r}$

donde a=primer término y r=razón común

Así, al sustituir el valor de a y r en esa fórmula

⇒ $(\frac{\frac13}{1-\frac1{3^2}}+\frac{\frac1{5^2}}{1-\frac1{5^2}})$

⇒ $(\frac{\frac13}{\frac8{3^2}}+\frac{\frac1{5^2}}{\frac{24}{5^2}})$

⇒ 3⁄8+1⁄24

⇒ 10⁄24

De este modo, $\frac13+\frac1{5^2}+\frac1{3^3}+\frac1{5^4}+\frac1{3^5}+\frac1{5^6}+....∞=\frac{10}{24}$

Pregunta 2: Demuestra que 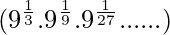$(9^{\frac13}.9^{\frac19}.9^{\frac1{27}}......∞)$

Solución:

Consideremos el lado izquierdo de la ecuación dada

⇒ $(9^{\frac13}.9^{\frac19}.9^{\frac1{27}}......∞)$

⇒ $9^{\frac13+\frac19+\frac1{27}....∞}$

La ecuación $\frac13+\frac19+\frac1{27}....∞$ está en forma de progresión geométrica donde el primer término = 1⁄3 y la razón común = 1⁄3

Sabemos que la suma de los términos de GP hasta el infinito es S= $\frac{a}{1-r}$

donde a=primer término y r=razón común

Así, al sustituir el valor de a y r en esa fórmula

⇒ $9^{\frac{\frac13}{1-\frac13}}$

⇒ $9^{\frac12}$

⇒ 3= Lado derecho de la ecuación dada

Así probamos que $(9^{\frac13}.9^{\frac19}.9^{\frac1{27}}......∞)=3$

Pregunta 3: Demuestra que 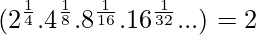$(2^{\frac14}.4^{\frac18}.8^{\frac1{16}}.16^{\frac1{32}}...∞)=2$

Solución:

Consideremos el lado izquierdo de la ecuación dada

sea S= $2^{\frac14}.4^{\frac18}.8^{\frac1{16}}.16^{\frac1{32}}...∞$

S= $2^{\frac14+\frac28+\frac3{16}+....∞}$

Denotando los términos en potencia con x

x= $\frac14+\frac28+\frac3{16}+.......∞$ ecuación-(1)

Podemos ver claramente que esta ecuación no está ni en GP ni en AP. Pero el numerador de esta ecuación está en AP y el denominador en GP

multipliquemos (1) por 1/2

$\frac12x=\frac12[\frac14+\frac28+\frac3{16}+.....∞]$ ecuación-(2)

Restemos (2) de (1)

$x-\frac{x}2=[\frac14+\frac28+\frac3{16}+....∞]-[\frac18+\frac2{16}+\frac3{32}+...∞]$

$\frac{x}2=\frac14+(\frac28-\frac18)+(\frac3{16}-\frac2{16})+...∞$

$\frac{x}2=\frac14+\frac18+\frac1{16}+...∞$

x= $\frac12+\frac14+\frac18+....∞$

Esta ecuación tiene la forma de progresión geométrica donde el primer término = 1/2 y la razón común = 1/2

Sabemos que la suma de los términos de GP hasta el infinito es S= $\frac{a}{1-r}$

donde a=primer término y r=razón común

Así, al sustituir el valor de a y r en esa fórmula

⇒x= $\frac{\frac12}{1-\frac12}$

⇒x= $\frac{\frac12}{\frac12}$

⇒x=1

⇒S=2=Lado derecho de la ecuación

Así probamos que $(2^{\frac14}.4^{\frac18}.8^{\frac1{16}}.16^{\frac1{32}}...∞)=2$

Pregunta 4: Si S _p denota la suma de la serie 1+r ^p +r ^2p +…….∞ y s _p la suma de la serie 1 – r ^p +r ^2p +…….∞. Demuestre que S _p + s _p = 2S _2p.

Solución:

Dado S _p =1+r ^p +r ^2p +…….∞

La ecuación anterior está en progresión geométrica donde el primer término = 1 y la razón común = r ^p

Sabemos que la suma de los términos de GP hasta el infinito es S= $\frac{a}{1-r}$

donde a=primer término y r=razón común donde r<1

Así, al sustituir el valor de a y r en esa fórmula

aquí |r|<1 ⇒|r ^p |<1

S _p = $\frac1{1-r^p}$ ecuación-(1)

y ^sp =1 – ^rp +r _2p +…….∞

La ecuación anterior está en progresión geométrica donde el primer término = 1 y la razón común = -r ^p

Sabemos que la suma de los términos de GP hasta el infinito es S= $\frac{a}{1-r}$

donde a=primer término y r=razón común donde r<1

Así, al sustituir el valor de a y r en esa fórmula

aquí |r|<1 ⇒|r ^p |<1

s _p = $\frac1{1+r^p}$ ecuación-(2)

al sumar (1) y (2)

S _pag +s _pag = $\frac1{1-r^p}+\frac1{1+r^p}$

= $\frac{1-r^p+1+r^p}{(1-r^p)(1+r^p)}$

= $\frac2{1-(r^p)^2}$

= $\frac2{1-r^{2p}}$ ecuación-(3)

De (1) podemos escribir $\frac1{1-r^{2p}}$ =S _2p

De (3), podemos escribir que S _p +s _p =2S _2p

Por lo tanto probado.

Pregunta 5: Encuentra la suma de los términos de un GP decreciente infinito en el que todos los términos son positivos, el primer término es 4 y la diferencia entre el tercer y quinto término es igual a 32⁄81

Solución:

Sea a el primer término de GP y r la razón común

sabemos que el enésimo término de un GP está dado por a _n =ar ^n-1

Dado a=4 y a ₅ -a ₃ = $\frac{32}{81}$

Aquí a ₅ = 4r ⁴ , a ₃ = 4r ²

⇒ 4r ⁴ -4r ² =32⁄81

⇒ 4r ² (r ² -1)=32⁄81

⇒ r ² (r ² -1)=8⁄81

sea x=r ²

⇒ x(x-1)=8⁄81

⇒ 81x ² -81x-8=0

al usar la fórmula de la ecuación cuadrática para resolver la ecuación anterior, obtenemos

x= $\frac{-(-81)\pm\sqrt{(81)^2-4(-8)(-81)}}{162}$

⇒x= $\frac{81\pm\sqrt{6561-2592}}{162}$

⇒ x=18⁄162 o x=144⁄162

⇒ x=1⁄9 o x=8⁄9

⇒ r ² = 1⁄9 o r ² = 8⁄9

⇒ r=1⁄3 o r=2√2/3

Sabemos que la suma de los términos de GP hasta el infinito es S= $\frac{a}{1-r}$

donde a=primer término y r=razón común

Tomemos el primer caso a=4 y r=1⁄3

Entonces, S= $\frac4{1-\frac13}$

⇒ S=6

Ahora, en el segundo caso a=4 y r= $\frac{2\sqrt{2}}3$

Entonces, S= $\frac4{1-\frac{2\sqrt2}3}$

⇒ S= $\frac{12}{3-2\sqrt2}$

Así, la suma de los términos de un GP decreciente infinito en el que todos los términos son positivos son 6 y $\frac{12}{3-2\sqrt2}$

Pregunta 6: Exprese el decimal periódico 0.125125125…. como un número racional.

Solución:

Sea x=0.125125125…… eq-(1)

Aquí 125 es el término repetido

Entonces, multipliquemos ambos lados de la ecuación con un número tal que la parte repetitiva completa del número venga después del decimal.

multipliquemos (1) por 1000 en ambos lados, obtenemos

1000x=125.125125125…… ecuación-(2)

restemos (1) de (2)

1000x-x=125.0000

999x=125

x=125⁄999

Así, 0.125125125…. se puede expresar como 125/999

Pregunta 7: Encuentra el número racional cuya expansión decimal es 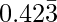$0.42\bar{3}$

Solución:

Sea x=0.423333333………… eq-(1)

aquí 3 es la parte que se repite.

Así que multipliquemos ambos lados de la ecuación (1) con un número tal que la parte repetitiva completa viene después del decimal

Multipliquemos (1) por 100

100x =42.33333………. ecuación-(2)

restemos (1) de (2)

100x-x=(42.3333333………..)-(0.4233333….)

99x = 41,91

x=41,91/99

x=4191/9900

El número racional cuya expansión decimal $0.42\bar{3}$ es 4191/9900

Pregunta 8-1: Encuentra el número racional que tiene la siguiente expansión decimal es 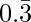$0.\bar3$

Solución:

sea x=0.333333333333………..

x=0.3+0.03+0.003+………∞

x=3(0.1+0.01+0.001+……..∞)

x= $3(\frac1{10}+\frac1{100}+\frac1{1000}+......∞)$

La ecuación anterior está en Progresión Geométrica con razón común=1⁄10 y primer término=1⁄10

Sabemos que la suma de los términos de GP hasta el infinito es S= $\frac{a}{1-r}$

donde a=primer término y r=razón común

Así, al sustituir el valor de a y r en esa fórmula

x= $3(\frac{\frac1{10}}{1-{\frac1{10}}})$

x=3×1⁄9

x=1⁄3

El número racional que tiene expansión decimal $0.\bar3$ es 1⁄3

Pregunta 8-2: Encuentra el número racional que tiene la siguiente expansión decimal es 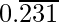$0.\overline{231}$

Solución:

sea x=0.231231231………. ecuación-(1)

x=0.231+0.000231+0.000000231+……..∞

x=231(0.001+0.00001+0.0000001+……∞)

x= $231(\frac1{10^3}+\frac1{10^6}+\frac1{10^9}+....∞)$

La ecuación anterior está en forma de progresión geométrica con el primer término = 1⁄1000 razón común = 1⁄1000

Sabemos que la suma de los términos de GP hasta el infinito es S= $\frac{a}{1-r}$

donde a=primer término y r=razón común

Así, al sustituir el valor de a y r en esa fórmula

x= $231(\frac{\frac1{1000}}{1-\frac1{1000}})$

= $231(\frac1{999})$

x=231/999

El número racional con expansión decimal $0.\overline{231}$ es 231/999

Pregunta 8-3: Encuentra el número racional que tiene la siguiente expansión decimal es 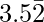$3.5\bar{2}$

Solución:

sea x=3.5222222……..

x=3,5+0,02+0,002+0,0002+…….∞

x=3,5+2(0,01+0,001+0,0001+…………∞)

sea s= 0.01+0.001+0.0001+…………∞

s= $\frac1{100}+\frac1{1000}+\frac1{10000}+........∞$

La ecuación anterior está en forma de progresión geométrica con el primer término = 1⁄100 y la razón común = 1⁄10

Sabemos que la suma de los términos de GP hasta el infinito es S= $\frac{a}{1-r}$

donde a=primer término y r=razón común

Así, al sustituir el valor de a y r en esa fórmula

s= $\frac{\frac1{100}}{1-\frac1{10}}$

s = 1⁄90

x=3.5+2s

=3.5+2×1⁄90

=35⁄10+1⁄45

=(315+2)/90

=317/90

El número racional con expansión decimal $3.5\bar{2}$ es 317/90.

Pregunta 8-4: Encuentra el número racional que tiene la siguiente expansión decimal es 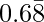$0.6\bar8$

Solución:

sea x=0.688888……….

x=0.6+0.08+0.008+0.0008+0.00008+…….∞

x=0.6+8(0.01+0.001+0.0001+……..∞)

sea s=0.01+0.001+0.0001+…………∞

s= $\frac1{100}+\frac1{1000}+\frac1{10000}+......∞$

La ecuación anterior está en forma de progresión geométrica con el primer término = 1⁄100 y la razón común = 1⁄10

Sabemos que la suma de los términos de GP hasta el infinito es S= $\frac{a}{1-r}$

donde a=primer término y r=razón común

Así, al sustituir el valor de a y r en esa fórmula

s= $\frac{\frac1{100}}{1-(\frac1{10})}$

=1⁄90

x=0.6+8s

=0.6+8×1⁄90

=62⁄90

El número racional que tiene expansión decimal $0.6\bar8$ es 62/90

Pregunta 9: Un lado de un triángulo equilátero mide 18 cm. Los puntos medios de los lados se unen para formar otro triángulo cuyos puntos medios, a su vez , se unen para formar otro triángulo más. El proceso continúa indefinidamente. Encuentra la suma de los (i) perímetros de todos los triángulos (ii) Áreas de todos los triángulos.

Solución:

Según el teorema del punto medio, los lados de cada triángulo formado al unir los puntos medios de un triángulo equilátero son la mitad de los lados del triángulo equilátero.

Así, los lados de los triángulos equiláteros formados son 18 cm, 9 cm, 4,5 cm, 2,25 cm, …………….

i) Suma de perímetros de todos los triángulos

Sea P la suma de los perímetros de todos los triángulos

P=3×18+3×9+3×4.5+3×2.25+………….∞

=3(18+9+9/2+9/4+……….∞)

Está en forma de GP con primer término=18 y razón común=1⁄2

Sabemos que la suma de los términos de GP hasta el infinito es S= $\frac{a}{1-r}$

donde a=primer término y r=razón común

P=3( $\frac{18}{1-\frac12}$ )

=3(18×2)

=3(36)=108

Por lo tanto, la suma de los perímetros de todos los triángulos = 108 cm

ii) Suma de Áreas de todos los triángulos

Sabemos que el área del triángulo equilátero =√3/4(a ² )

donde a es la longitud del lado del triángulo equilátero.

Sea A la suma de las áreas de todos los triángulos

A= √3/4(18) ² +√3/4(9) ² +√3/4(4.5) ² +√3/4(2.25) ² +……………….∞

=√3/4((18) ² +(9) ² +(4.5) ² +(2.25) ² +…………∞)

Está en forma de GP con primer término=(18) ² y razón común=1⁄4

Sabemos que la suma de los términos de GP hasta el infinito es S= $\frac{a}{1-r}$

A= $\frac{\sqrt3}4(\frac{18^2}{1-\frac14})$

= (√3/3)×18 ²

= 324/√3

⁼ 108√3cm2

Por tanto, la Suma de las Áreas de todos los triángulos =108√3cm ²

Pregunta 10: Encuentra un GP infinito cuyo primer término sea 1 y cada término sea la suma de todos los términos que le siguen

Solución:

Dado el primer término = 1

Sea r la razón común

También dado cada término es la suma de todos los términos que le siguen

⇒ un _norte =[un _norte+1 +un norte ₊₂ +un norte ₊₃ +………………∞] ∀ norte∈ norte

⇒ ar ^n-1 =ar ⁿ +ar ⁿ⁺¹ +ar ⁿ⁺² +……………..∞ [ya que hay en GP]

⇒ rn ^-1 = rn +rn+ ¹ + rn ⁺² + ………… ^..∞

⇒ rn ^-1 = $\frac{r^n}{1-r}$

⇒ rn ^-1 (1-r)= ^rn

⇒ rn ^–¹ -rn = ^rn

⇒rn ^-1 = ^2rn

⇒ 1=2r

⇒r=1⁄2

Ahora, la serie infinita será a,ar,ar ² ,ar ³ ………..∞

Y así el GP infinito es 1,1⁄2,1⁄4,1⁄8,…………………….∞

Pregunta 11: La suma de los dos primeros términos de GP infinito es 5 y cada término es tres veces la suma de los términos sucesivos. Encuentra el médico de cabecera

Solución:

Sea el primer término a y la diferencia común sea r en un GP infinito dado

Dado un ₁ + un ₂ = 5

⇒ a+ar=5 -(yo)

Además, Dado, a _n =3[a _n+1 +a _n+2 +a _n+3 +………∞] ∀ n∈ N

⇒ arn ^-1 =3[arn ^+1-1 +arn ^+2-1 + arn ^+3-1 +………..∞]

=3[ arn +arn+1 + arn ⁺²⁺ ………… .∞ ^]

=3ar ⁿ [1+r+r ² +………….∞]

=3ar ⁿ \frac1{1-r}

ar ^n-1 =3ar ⁿ \frac1{1-r}

⇒ r ^-1 =3⁄1-r

⇒ 1-r=3r

⇒ 1=4r

⇒r=1⁄4

Al sustituir el valor de r en (i)

⇒ a+a(1⁄4)=5

⇒ a(1+1⁄4)=5

⇒ a(5⁄4)=5

⇒ a=4

Ahora, los términos de GP serán a,ar,ar ² ,ar ³ ,………………∞

Así, los términos de GP serán 4,1,1⁄4,1⁄16…………∞

Pregunta 12: Muestre que en un GP infinito con una razón común r(|r|<1), cada término tiene una razón constante a la suma de todos los términos que le siguen.

Solución:

Consideremos una serie GP infinita cuyos términos son a ₁ ,a ₂ ,a ₃ ,a ₄ ,a ₅ …………∞ y razón común r(|r|<1).

Además, supongamos que la suma de todos los términos que siguen a cada término será S ₁ ,S ₂ ,S ₃ ,S ₄ ………….∞

sabemos que 1+r+r ² +r ³ +r ⁴ +………………..∞=1⁄1-r

Ahora, S ₁ = $\frac{a_2}{1-r}$ = $\frac{ar}{1-r}$

S ₂ = $\frac{a_3}{1-r}$ = $\frac{ar^2}{1-r}$

S ₃ = $\frac{a_4}{1-r}$ = $\frac{ar^3}{1-r}$

⇒ a ₁ /S ₁ = $\frac{a}{\frac{ar}{(1-r)}}$ =(1-r)/r

⇒a ₂ /S ₂ = $\frac{ar}{\frac{ar^2}{(1-r)}}$ =(1-r)/r

⇒ a ₃ /S ₃ = $\frac{ar^2}{\frac{ar^3}{(1-r)}}$ =(1-r)/r

Podemos observar claramente que a _n /S _n =constante

Así, demostramos que la razón de cada término a la suma de todos los términos que le siguen son constantes.

Pregunta 13: Si S denota la suma de infinitos GP S ₁ denota la suma de los cuadrados de sus elementos, entonces demuestre que el primer término y la razón común son respectivamente 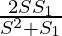$\frac{2SS_1}{S^2+S_1}$ y $\frac{S^2-S_1}{S^2+S_1}$

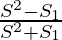
Solución:

Consideremos una serie GP infinita

Sea a el primer término y r la razón común en la serie GP.

Dado

a+ar+ar ² +ar ³ +…………..∞=S

⇒ a(1+r+r ² +r ³ +…………..∞)=S

⇒ a(1⁄1-r)=S    eq-(1)

también dado

S ₁ =a ² +a ² r ² +a ² r ⁴ +…………..∞

=a ² (1+r ² +r ⁴ +………….∞)

= un ² ( $\frac1{1-r^2}$ )

= $\frac{a}{1+r}$ × $\frac{a}{1-r}$

S ₁ =S×( $\frac{a}{1+r}$ )    ecuación-(2)

Divida (2) por (1)

_{S1 /} S = $\frac{\frac{aS}{1+r}}{\frac{a}{1-r}}$

= $\frac{S}{\frac{1+r}{1-r}}$

   $\frac{S_1}{S^2}=\frac{1-r}{1+r}$

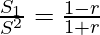
⇒ (1-r)S ² =(1+r)S ₁

⇒ S ² -S ₁ =r(S ² +S ₁ )

⇒r= $\frac{S^2-S_1}{S^2+S_1}$

Al sustituir el valor de r en (1)

S= $\frac{a}{1-\frac{{S^2-S_1}}{{S^2+S_1}}}$

S = $\frac{a{(S^2+S_1)}}{S^2+S_1-(S^2-S_1)}$

S= $\frac{a(S^2+S_1)}{2S_1}$

2SS ₁ =a(S ² +S ₁ )

⇒ a= $\frac{2SS_1}{S^2+S_1}$

Así, probamos que a= $\frac{2SS_1}{S^2+S_1}$ y r= $\frac{S^2-S_1}{S^2+S_1}$

Publicación traducida automáticamente

Artículo escrito por prasanthinidamarthy y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1.1 Encuentra la suma de las siguientes series hasta el infinito:

Pregunta 1.2 Encuentra la suma de las siguientes series hasta el infinito:

Pregunta 1.3 Encuentra la suma de las siguientes series hasta el infinito:

Pregunta 1.4 Encuentra la suma de las siguientes series hasta el infinito: 10-9+8.1-7.29+……….∞

Pregunta 1.5 Encuentra la suma de las siguientes series hasta el infinito:

Pregunta 2: Demuestra que

Pregunta 3: Demuestra que

Pregunta 4: Si S p denota la suma de la serie 1+r p +r 2p +…….∞ y s p la suma de la serie 1 – r p +r 2p +…….∞. Demuestre que S p + s p = 2S 2p.

Pregunta 5: Encuentra la suma de los términos de un GP decreciente infinito en el que todos los términos son positivos, el primer término es 4 y la diferencia entre el tercer y quinto término es igual a 32⁄81

Pregunta 6: Exprese el decimal periódico 0.125125125…. como un número racional.

Pregunta 7: Encuentra el número racional cuya expansión decimal es

Pregunta 8-1: Encuentra el número racional que tiene la siguiente expansión decimal es

Pregunta 8-2: Encuentra el número racional que tiene la siguiente expansión decimal es

Pregunta 8-3: Encuentra el número racional que tiene la siguiente expansión decimal es

Pregunta 8-4: Encuentra el número racional que tiene la siguiente expansión decimal es

Pregunta 10: Encuentra un GP infinito cuyo primer término sea 1 y cada término sea la suma de todos los términos que le siguen

Pregunta 11: La suma de los dos primeros términos de GP infinito es 5 y cada término es tres veces la suma de los términos sucesivos. Encuentra el médico de cabecera

Pregunta 12: Muestre que en un GP infinito con una razón común r(|r|<1), cada término tiene una razón constante a la suma de todos los términos que le siguen.

Pregunta 13: Si S denota la suma de infinitos GP S 1 denota la suma de los cuadrados de sus elementos, entonces demuestre que el primer término y la razón común son respectivamente y

Deja una respuesta Cancelar la respuesta

Pregunta 1.1 Encuentra la suma de las siguientes series hasta el infinito: $1-\frac13+\frac1{3^2}-\frac1{3^3}+\frac1{3^4}+......∞$

Pregunta 1.2 Encuentra la suma de las siguientes series hasta el infinito: $8+4\sqrt2+4+..........∞$

Pregunta 1.3 Encuentra la suma de las siguientes series hasta el infinito: $\frac25+\frac3{5^2}+\frac2{5^3}+\frac3{5^4}+.......∞$

Pregunta 1.5 Encuentra la suma de las siguientes series hasta el infinito: $\frac13+\frac1{5^2}+\frac1{3^3}+\frac1{5^4}+\frac1{3^5}+\frac1{5^6}+....∞$

Pregunta 2: Demuestra que $(9^{\frac13}.9^{\frac19}.9^{\frac1{27}}......∞)$

Pregunta 3: Demuestra que $(2^{\frac14}.4^{\frac18}.8^{\frac1{16}}.16^{\frac1{32}}...∞)=2$

Pregunta 4: Si S _p denota la suma de la serie 1+r ^p +r ^2p +…….∞ y s _p la suma de la serie 1 – r ^p +r ^2p +…….∞. Demuestre que S _p + s _p = 2S _2p.

Pregunta 7: Encuentra el número racional cuya expansión decimal es $0.42\bar{3}$

Pregunta 8-1: Encuentra el número racional que tiene la siguiente expansión decimal es $0.\bar3$

Pregunta 8-2: Encuentra el número racional que tiene la siguiente expansión decimal es $0.\overline{231}$

Pregunta 8-3: Encuentra el número racional que tiene la siguiente expansión decimal es $3.5\bar{2}$

Pregunta 8-4: Encuentra el número racional que tiene la siguiente expansión decimal es $0.6\bar8$

Pregunta 13: Si S denota la suma de infinitos GP S ₁ denota la suma de los cuadrados de sus elementos, entonces demuestre que el primer término y la razón común son respectivamente $\frac{2SS_1}{S^2+S_1}$ y $\frac{S^2-S_1}{S^2+S_1}$