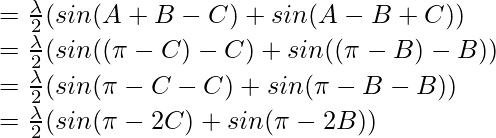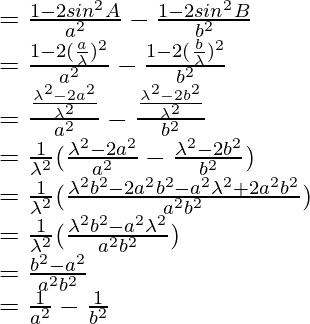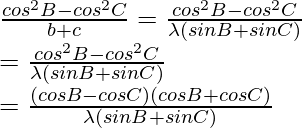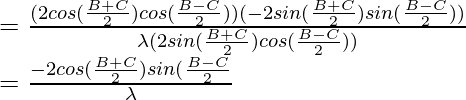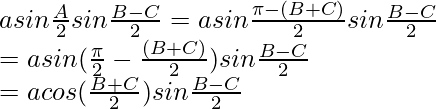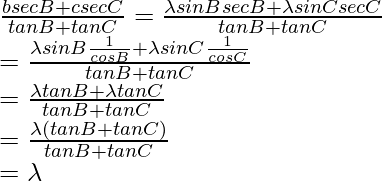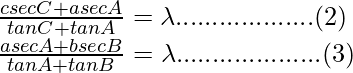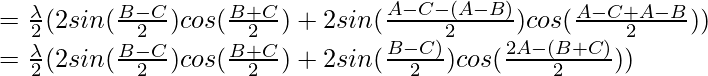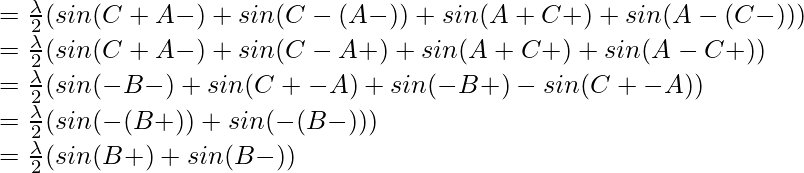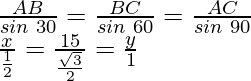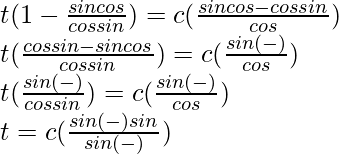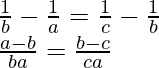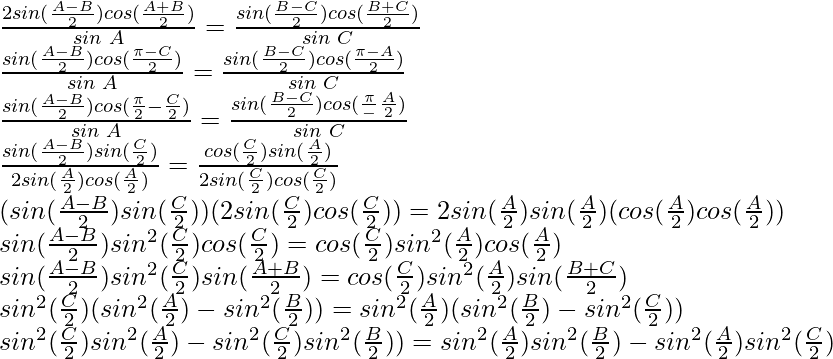Clase 11 Soluciones RD Sharma – Capítulo 10 Fórmulas de seno y coseno y sus aplicaciones – Ejercicio 10.1 | conjunto 2

Posted on by Rudeus Greyrat

Pregunta 16: En △ABC, prueba lo siguiente:

a 2 (cos 2 B – cos 2 C) + b (cos 2 C – cos 2 A) + c (cos 2 A – cos 2 B) = 0

Solución:

Según la regla del seno

\frac{a}{sin \hspace{0.1cm}A} = \frac{b}{sin \hspace{0.1cm}B} = \frac{c}{sin \hspace{0.1cm}C} = \lambda

Considerando LHS, tenemos

= a 2 (cos 2 B – cos 2 C) + b (cos 2 C – cos 2 A) + c (cos 2 A – cos 2 B)

Usando la fórmula trigonométrica,

cos 2 a = 1 – sen 2 a

= λ 2 sen 2 A(1-sen 2 B – (1-sen 2 C)) + λ 2 sen 2 B(1-sen 2 C – (1-sen 2 A)) + λ 2 sen 2 C(1 -sen 2 A – (1-sen 2 B))

= λ 2 sen 2 A(1-sen 2 B – 1+ sen 2 C) + λ 2 sen 2 B(1-sen 2 C – 1 + sen 2 A) + λ 2 sen 2 C(1-sen 2 A – 1+sen 2 B)

= λ 2 sen 2 A (sen 2 C – sen 2 B) + λ 2 sen 2 B (sen 2 A – sen 2 C) + λ 2 sen 2 C (sen 2 B – sen 2 A)

= λ 2 (sen 2 A sen 2 C – sen 2 A sen 2 B + sen 2 B sen 2 A – sen 2 B sen 2 C+ sen 2 C sen 2 B – sen 2 C sen 2 A)

= λ2 ( 0 )

=0

Como LHS = RHS

Por lo tanto, probado!!

Pregunta 17: En △ABC, prueba lo siguiente:

b porque B + c porque C = a porque (BC)

Solución:

Según la regla del seno

\frac{a}{sin \hspace{0.1cm}A} = \frac{b}{sin \hspace{0.1cm}B} = \frac{c}{sin \hspace{0.1cm}C} = \lambda

Considerando LHS, tenemos

= b cos B + c cos C

= λ sen B cos B + λ sen C cos C

= λ (sen B cos B + sen C cos C)

= \frac{\lambda}{2} (2 sen B cos B + 2 sen C cos C)

Usando la fórmula trigonométrica,

2 sen a cos a = sen 2a

= \frac{\lambda}{2} (sen 2B + sen 2C) ………………………..(1)

Ahora considerando RHS, tenemos

= a porque (BC)

= λ sen A cos (BC)

= \frac{\lambda}{2} (2 sen A cos (BC))

Usando la fórmula trigonométrica,

2 sen a cos b = sen (a+b) + sen(ab)

= \frac{\lambda}{2}(sin (A+B-C) + sin(A-B+C))\\ = \frac{\lambda}{2}(sin ((\pi-C)-C) + sin((\pi-B)-B))\\ = \frac{\lambda}{2}(sin (\pi-C-C) + sin(\pi-B-B))\\ = \frac{\lambda}{2}(sin (\pi-2C) + sin(\pi-2B))

= \frac{\lambda}{2} (sen 2C+ sen 2B) ……………………….(2)

Como LHS = RHS

Por lo tanto, probado!!

Pregunta 18: En △ABC, prueba lo siguiente:

\frac{cos(2A)}{a^2} - \frac{cos(2B)}{b^2} = \frac{1}{a^2} - \frac{1}{b^2}

Solución:

Según la regla del seno

\frac{a}{sin \hspace{0.1cm}A} = \frac{b}{sin \hspace{0.1cm}B} = \frac{c}{sin \hspace{0.1cm}C} = \lambda

Considerando LHS, tenemos

= \frac{cos(2A)}{a^2} - \frac{cos(2B)}{b^2}

Usando la fórmula trigonométrica,

cos 2a = 1-2sen 2 a

= \frac{1-2sin^2A}{a^2} - \frac{1-2sin^2B}{b^2}\\ = \frac{1-2(\frac{a}{\lambda})^2}{a^2} - \frac{1-2(\frac{b}{\lambda})^2}{b^2}\\ = \frac{\frac{\lambda^2-2a^2}{\lambda^2}}{a^2} - \frac{\frac{\lambda^2-2b^2}{\lambda^2}}{b^2}\\ = \frac{1}{\lambda^2}(\frac{\lambda^2-2a^2}{a^2} - \frac{\lambda^2-2b^2}{b^2})\\ = \frac{1}{\lambda^2}(\frac{\lambda^2b^2-2a^2b^2 - a^2\lambda^2+2a^2b^2}{a^2b^2})\\ = \frac{1}{\lambda^2}(\frac{\lambda^2b^2- a^2\lambda^2}{a^2b^2})\\ = \frac{b^2- a^2}{a^2b^2}\\ = \frac{1}{a^2} - \frac{1}{b^2}

Como LHS = RHS

Por lo tanto, probado!!

Pregunta 19: En △ABC, prueba lo siguiente:

\frac{cos^2B-cos^2C}{b+c} + \frac{cos^2C-cos^2A}{c+a} + \frac{cos^2A-cos^2B}{a+b} = 0

Solución:

Según la regla del seno

\frac{a}{sin \hspace{0.1cm}A} = \frac{b}{sin \hspace{0.1cm}B} = \frac{c}{sin \hspace{0.1cm}C} = \lambda

Considerando LHS, tenemos

= \frac{cos^2B-cos^2C}{b+c} + \frac{cos^2C-cos^2A}{c+a} + \frac{cos^2A-cos^2B}{a+b}

Ahora tomando,

\frac{cos^2B-cos^2C}{b+c} = \frac{cos^2B-cos^2C}{\lambda(sin B + sin C)}\\ = \frac{cos^2B-cos^2C}{\lambda(sin B + sin C)}\\ = \frac{(cosB-cosC)(cosB+cosC)}{\lambda(sin B + sin C)}

Usando la fórmula trigonométrica,

cos a + cos b = 2 cos (\frac{a+b}{2}) cos(\frac{a-b}{2})

cos a – cos b = -2 sen (\frac{a+b}{2}) sen(\frac{a-b}{2})

sen a + sen b = 2 sen (\frac{a+b}{2}) cos(\frac{a-b}{2})

= \frac{(2 cos (\frac{B+C}{2}) cos(\frac{B-C}{2}))(-2 sin (\frac{B+C}{2}) sin(\frac{B-C}{2}))}{\lambda(2 sin (\frac{B+C}{2}) cos(\frac{B-C}{2}))}\\ = \frac{- 2 cos (\frac{B+C}{2}) sin (\frac{B-C}{2}}{\lambda}

Usando la fórmula trigonométrica,

2 porque (\frac{a+b}{2}) sen (\frac{a-b}{2}) = sen a – sen b

= \frac{- (sin B - sin C)}{\lambda}

= \frac{sin C - sin B}{\lambda} ………………(1)

Del mismo modo, podemos probar,

\frac{cos^2C-cos^2A}{c+a} = \frac{sin A - sin C}{\lambda} ……………….(2)

\frac{cos^2A-cos^2B}{a+b} = \frac{sin B - sin A}{\lambda} ………………..(3)

Sumando (1), (2) y (3), obtenemos

\frac{sin C - sin B}{\lambda} + \frac{sin A - sin C}{\lambda} + \frac{sin B - sin A}{\lambda}

= 0

Como LHS = RHS

Por lo tanto, probado!!

Pregunta 20: En △ABC, prueba lo siguiente:

a sin \frac{A}{2} sin \frac{B-C}{2} + b sin\frac{B}{2} sin \frac{C-A}{2} + c sin\frac{C}{2} sin \frac{A-B}{2} = 0

Solución:

Según la regla del seno

\frac{a}{sin \hspace{0.1cm}A} = \frac{b}{sin \hspace{0.1cm}B} = \frac{c}{sin \hspace{0.1cm}C} = \lambda

Considerando LHS, tenemos

= a sin \frac{A}{2} sin \frac{B-C}{2} + b sin\frac{B}{2} sin \frac{C-A}{2} + c sin\frac{C}{2} sin \frac{A-B}{2}

Ahora tomando,

a sin \frac{A}{2} sin \frac{B-C}{2} = a sin \frac{\pi-(B+C)}{2} sin \frac{B-C}{2}\\ = a sin (\frac{\pi}{2}-\frac{(B+C)}{2}) sin \frac{B-C}{2}\\ = a cos (\frac{B+C}{2}) sin \frac{B-C}{2}

= \frac{2}{2} a porque (\frac{B+C}{2}) pecado(\frac{B-C}{2})

= \frac{1}{2} (sen B – sen C)

= \frac{1}{2} (un pecado B – un pecado C)

= \frac{1}{2} (un pecado B – un pecado C)

= \frac{1}{2} (b sen A – a sen C) ………………..(1)

Del mismo modo, podemos probar,

b sin\frac{B}{2} sen (\frac{C-A}{2}) = \frac{1}{2} (b sen C – b sen A) ……………….(2)

c sin\frac{C}{2} sen (\frac{A-B}{2}) = \frac{1}{2} (a sen C – b sen C) ………………..(3)

Sumando (1), (2) y (3), obtenemos

\frac{1}{2} (b sen A – a sen C) + \frac{1}{2} (b sen C – b sen A) + \frac{1}{2} (a sen C – b sen C)

= \frac{1}{2} (b sen A – a sen C+ b sen C – b sen A + a sen C – b sen C)

= 0

Como LHS = RHS

Por lo tanto, probado!!

Pregunta 21: En △ABC, prueba lo siguiente:

\frac{b secB+c sec C}{tan B +tan C} = \frac{c sec C+ a sec A}{tan C +tan A} = \frac{a secA+b sec B}{tan A +tan B}

Solución:

Según la regla del seno

\frac{a}{sin \hspace{0.1cm}A} = \frac{b}{sin \hspace{0.1cm}B} = \frac{c}{sin \hspace{0.1cm}C} = \lambda

Teniendo en cuenta la ecuación, tenemos

\frac{b secB+c sec C}{tan B +tan C} = \frac{c sec C+ a sec A}{tan C+tan A} = \frac{a secA+b sec B}{tan A +tan B}

Ahora tomando,

\frac{b secB+c sec C}{tan B +tan C} = \frac{\lambda sin B secB+ \lambda sin C sec C}{tan B +tan C}\\ = \frac{\lambda sin B \frac{1}{cos B} + \lambda sin C \frac{1}{cos C}}{tan B +tan C}\\ = \frac{\lambda tan B+ \lambda tan C}{tan B +tan C}\\ = \frac{\lambda (tan B+tan C)}{tan B +tan C}\\ = \lambda

Del mismo modo, podemos probar,

\frac{c sec C+ a sec A}{tan C+tan A} = \lambda ...................(2)\\ \frac{a secA+b sec B}{tan A +tan B} = \lambda ....................(3)

De (1), (2) y (3), obtenemos

\frac{b secB+c sec C}{tan B +tan C} = \frac{c sec C+ a sec A}{tan C+tan A} = \frac{a secA+b sec B}{tan A +tan B}

Por lo tanto, probado!!

Pregunta 22: En △ABC, prueba lo siguiente:

a cos A + b cos B + c cos C = 2b sen A sen C = 2c sen A sen B

Solución:

Según la regla del seno

\frac{a}{sin \hspace{0.1cm}A} = \frac{b}{sin \hspace{0.1cm}B} = \frac{c}{sin \hspace{0.1cm}C} = \lambda

Considerando la ecuación LHS, tenemos

a cos A + b cos B + c cos C = λ sen A cos A + λ sen B cos B + λ sen C cos C

= λ (sen A cos A + sen B cos B + sen C cos C)

= \frac{2\lambda}{2} (sen A cos A + sen B cos B + sen C cos C)

= \frac{\lambda}{2} (2 sen A cos A + 2 sen B cos B + 2 sen C cos C)

Usando la fórmula trigonométrica,

2 sen a cos a = sen 2a

= \frac{\lambda}{2} (sen 2A + sen 2B + 2 sen C cos C)

Usando la fórmula trigonométrica,

sen a + sen b = 2 sen (\frac{a+b}{2}) cos(\frac{a-b}{2})

= \frac{\lambda}{2} (2 sin (\frac{2A+2B}{2}) cos(\frac{2A-2B}{2}) + 2 sen C cos C)

= \frac{\lambda}{2} (2 sen (A+B) cos(AB) + 2 sen C cos C)

= \frac{\lambda}{2} (2 sen (π-C) cos(AB) + 2 sen C cos C)

= \frac{\lambda}{2} (2 sen C cos(AB) + 2 sen C cos C)

= \frac{2\lambda sinC}{2} (cos(AB) + cos C)

= λ sen C (cos(AB) + cos (π-(A+B)))

= λ sen C (cos(AB) + (-cos (A+B)))

= λ sen C (cos(AB) – cos (A+B))

= λ sen C (2 sen A sen B)

= 2 λ sen A sen B sen C

Ahora, poniendo λ sin C = c y λ sin B = b, obtenemos

2 c sen A sen B y 2 b sen A sen C

Por lo tanto, probado!!

Pregunta 23: En △ABC, prueba lo siguiente:

a (cos B cos C+ cos A) = b (cos C cos A + cos B) = c (cos C cos A + cos C)

Solución:

Según la regla del seno

\frac{a}{sin \hspace{0.1cm}A} = \frac{b}{sin \hspace{0.1cm}B} = \frac{c}{sin \hspace{0.1cm}C} = \lambda

Teniendo en cuenta la ecuación, tenemos

a (cos B cos C+ cos A) = λ sen A (cos B cos C+ cos A)

= λ (sen A cos B cos C+ sen A cos A)

= λ ( \frac{cos C}{2} (2 sen A cos B) + sen A cos A)

= λ ( \frac{cos C}{2} (sin (A+B) + sin (AB)) + sin A cos A)

= λ ( \frac{1}{2} (cos C sen (A+B) + cos C sen (AB)) + sen A cos A)

= λ ( \frac{1}{2} (\frac{1}{2} (2 cos C sen (A+B) + 2 cos C sen (AB))) + sen A cos A)

= λ ( \frac{1}{2} (2 cos C sen (A+B) + 2 cos C sen (AB)) + sen A cos A)

Usando la fórmula trigonométrica,

2 sen a cos b = sen (a+b) + sen (ab)

= λ ( \frac{1}{4} (sin (A+B+C) + sin (A+BC) + sin (A-B+C) + sin (ABC)) + sin A cos A)

= λ ( \frac{1}{4} (sin (π) + sin ((π-C)-C) + sin ((π-B)-B) + sin (A-(B+C)) + \frac{sin 2A}{2} )

= λ ( \frac{1}{4} (0 + sen (π-2C) + sen (π-2B) + sen (2A-π) + \frac{sin 2A}{2} )

= λ ( \frac{1}{4} (sen 2C+ sen 2B – sen 2A + \frac{sin 2A}{2} )

= \frac{\lambda}{4} (sen 2C+ sen 2B + sen 2A)

Similarmente,

b (cos C cos A + cos B) = \frac{\lambda}{4} (sen 2C+ sen 2B + sen 2A)

c (cos C cos A + cos C) = \frac{\lambda}{4} (sen 2C+ sen 2B + sen 2A)

Por lo tanto, probado!!

Pregunta 24: En △ABC, prueba lo siguiente:

a (cos C – cos B) = 2 (bc)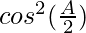cos^2(\frac{A}{2})

Solución:

Según la regla del seno

\frac{a}{sin \hspace{0.1cm}A} = \frac{b}{sin \hspace{0.1cm}B} = \frac{c}{sin \hspace{0.1cm}C} = \lambda

Teniendo en cuenta la ecuación, tenemos

a (cos C – cos B) = λ sin A (cos C – cos B)

= λ (sen A cos C – sen A cos B)

= \frac{\lambda}{2} (2 sen A cos C – 2 sen A cos B)

Usando la fórmula trigonométrica,

2 sen a cos b = sen (a+b) + sen (ab)

= \frac{\lambda}{2} (sin (A+C) + sin (AC) – (sin (A+B) + sin (AB)))

= \frac{\lambda}{2} (sin (A+C) + sin (AC) – sin (A+B) – sin (AB))

= \frac{\lambda}{2} (sen (π-B) + sen (AC) – sen (π-C) – sen (AB))

= \frac{\lambda}{2} (sen B – sen C+ sen (AC) – sen (AB))

Usando la fórmula trigonométrica,

sen a – sen b = 2 sen (\frac{a-b}{2}) cos(\frac{a+b}{2})

= \frac{\lambda}{2} (2 sin (\frac{B-C}{2}) cos(\frac{B+C}{2}) + 2 sin (\frac{A-C-(A-B)}{2}) cos(\frac{A-C+A-B}{2}))\\ = \frac{\lambda}{2} (2 sin (\frac{B-C}{2}) cos(\frac{B+C}{2}) + 2 sin (\frac{B-C)}{2}) cos(\frac{2A-(B+C)}{2}))

= λsin (\frac{B-C}{2}) (cos(\frac{\pi-A}{2}) + cos(\frac{\pi-3A}{2}))

= λsin (\frac{B-C}{2}) (cos(\frac{π}{2}-\frac{A}{2}) + cos(\frac{π}{2}-\frac{3A}{2}))

= λ sen(\frac{B-C}{2}) (sin(\frac{A}{2}) + sin(\frac{3A}{2}))

Usando la fórmula trigonométrica,

sen a + sen b = 2 sen (\frac{a+b}{2}) cos(\frac{a-b}{2})

= λ sen(\frac{B-C}{2})
(2 sin (\frac{\frac{3A}{2}+\frac{A}{2}}{2}) cos(\frac{\frac{3A}{2}-\frac{A}{2}}{2}))

= λ sen(\frac{B-C}{2})
(2 sin (\frac{\frac{4A}{2}}{2}) cos(\frac{\frac{2A}{2}}{2}))

= λ sen (\frac{B-C}{2}) (2 sen A cos (\frac{A}{2}) )

= 2 λ sen (\frac{B-C}{2}) (2 sen (\frac{A}{2}) cos (\frac{A}{2}) ) cos(\frac{A}{2})

= 4 λ sen (\frac{B-C}{2}) sen (\frac{A}{2}) [Tex]cos^2(\frac{A}{2})[/Tex]

= 4 λ sen (\frac{B-C}{2}) cos (\frac{\pi}{2}-\frac{A}{2}) [Tex]cos^2(\frac{A}{2})[/Tex]

= 4 λ sen (\frac{B-C}{2}) cos (\frac{\pi-A}{2}) [Tex]cos^2(\frac{A}{2})[/Tex]

= 4 λ sen (\frac{B-C}{2}) cos (\frac{B+C}{2}) [Tex]cos^2(\frac{A}{2})[/Tex]

= 2 λ (2 sen (\frac{B-C}{2}) cos (\frac{B+C}{2}) )cos^2(\frac{A}{2})

Usando la fórmula trigonométrica,

2 porque (\frac{a+b}{2}) sen (\frac{a-b}{2}) = sen a – sen b

= 2 λ (sen B – sen A)cos^2(\frac{A}{2})

= 2 (λ sen B – λ sen A)cos^2(\frac{A}{2})

= 2 (b – a)cos^2(\frac{A}{2})

Como LHS = RHS

Por lo tanto, probado!!

Pregunta 25: En △ABC, prueba lo siguiente:

b cos θ = c cos(A-θ)+a cos(C+θ)

Solución:

Según la regla del seno

\frac{a}{sin \hspace{0.1cm}A} = \frac{b}{sin \hspace{0.1cm}B} = \frac{c}{sin \hspace{0.1cm}C} = \lambda

Considerando RHS, ecuación, tenemos

c cos(A-θ)+a cos(C+θ) = λ sen C cos(A-θ) + λ sen A cos(C+θ)

= λ (sen C cos(A-θ) + sen A cos(C+θ))

=\frac{\lambda}{2} (2 sin C cos(A-θ) + 2 sin A cos(C+θ))

Usando la fórmula trigonométrica,

2 sen a cos b = sen (a+b) + sen (ab)

= \frac{\lambda}{2} (sin (C+A-θ) + sin (C-(A-θ)) + sin (A+C+θ) + sin (A-(C-θ)))\\ = \frac{\lambda}{2} (sin (C+A-θ) + sin (C-A+θ) + sin (A+C+θ) + sin (A-C+θ))\\ = \frac{\lambda}{2} (sin (π-B-θ) + sin (C+θ-A) + sin (π-B+θ) - sin (C+θ-A))\\ = \frac{\lambda}{2} (sin (π-(B+θ)) + sin (π-(B-θ)))\\ = \frac{\lambda}{2} (sin (B+θ) + sin (B-θ))

Usando la fórmula trigonométrica,

sen (a+b) + sen (ab) = 2 sen a cos b

=\frac{\lambda}{2} (2 sin B cos θ)

= λ sen B cos θ

= b cos θ

Como LHS = RHS

Por lo tanto, probado!!

Pregunta 26: En △ABC, si sen 2 A + sen 2 B = sen 2 C. Demuestra que el triángulo es rectángulo.

Solución:

Según la regla del seno

\frac{a}{sin \hspace{0.1cm}A} = \frac{b}{sin \hspace{0.1cm}B} = \frac{c}{sin \hspace{0.1cm}C} = \lambda

Teniendo en cuenta la ecuación, tenemos

sen 2 A + sen 2 B = sen 2 C

(\frac{a}{\lambda})^2 + (\frac{b}{\lambda})^2 = (\frac{c}{\lambda})^2

un 2 + segundo 2 = do 2

Por lo tanto, probado, el triángulo es rectángulo como c como hipotenusa.

Pregunta 27: En △ABC, si a 2 , b 2 y c 2 están en AP. Demuestre que la cuna A, la cuna B y la cuna C también están en AP.

Solución:

Tenemos a 2 , b 2 y c 2 en AP

2a 2 , 2b 2 y 2c 2 también están en AP

(a 2 +b 2 +c 2 )-2a 2 , (a 2 +b 2 +c 2 )-2b 2 y (a 2 +b 2 +c 2 )-2c 2 también están en AP

b 2 +c 2 -a 2 , a 2 +c 2 -b 2 y a 2 +b 2 -c 2 también están en AP

\frac{b^2+c^2-a^2}{2abc} , \frac{a^2+c^2-b^2}{2abc} y \frac{a^2+b^2-c^2}{2abc} también están en AP

\frac{1}{a}(\frac{b^2+c^2-a^2}{2bc}) , \frac{1}{b}(\frac{a^2+c^2-b^2}{2ac}) y \frac{1}{c}(\frac{a^2+b^2-c^2}{2ab}) también están en AP

Según la regla del coseno

cos A = \frac{b^2+c^2-a^2}{2bc}

\frac{1}{a}(cos A) , \frac{1}{b}(cos B) y \frac{1}{c}(cos C) también están en AP

\frac{\lambda}{a}(cos A) , \frac{\lambda}{a}(cos B) y \frac{\lambda}{a}(cos C) también están en AP

Según la regla del seno

\frac{a}{sin \hspace{0.1cm}A} = \frac{b}{sin \hspace{0.1cm}B} = \frac{c}{sin \hspace{0.1cm}C} = \lambda

\frac{cos A}{sin A} , \frac{cos B}{sin B} y \frac{cos C}{sin C} también están en AP

la cuna A, la cuna B y la cuna C también están en AP

Por lo tanto, probado !!

Pregunta 28: La parte superior de un árbol quebrado por el viento forma un ángulo de 30° con el suelo y la distancia desde la raíz hasta el punto donde la copa del árbol toca el suelo es de 15 m. Usando la regla del seno, encuentre la altura del árbol.

Solución:

Suponga que BD es el árbol y la parte superior del árbol es rota por el viento en el punto A.

La altura total del árbol es x+y.

En △ABC, ∠C = 30° y ∠B = 90°

∠A = 60° ( propiedad de la suma de los ángulos del triángulo )

Según la regla del seno

\frac{AB}{sin \hspace{0.1cm}30\degree} = \frac{BC}{sin \hspace{0.1cm}60\degree} = \frac{AC}{sin \hspace{0.1cm}90\degree}\\ \frac{x}{\frac{1}{2}} = \frac{15}{\frac{\sqrt{3}}{2}} = \frac{y}{1}

2x = \frac{30}{\sqrt{3}} = y

Por lo tanto, x = \frac{30}{2\sqrt{3}} = \frac{15}{\sqrt{3}} = \frac{15}{\sqrt{3}}\times\frac{\sqrt{3}}{\sqrt{3}} = \frac{15\sqrt{3}}{3} = 5√3

y y = \frac{30}{\sqrt{3}}\times\frac{\sqrt{3}}{\sqrt{3}} = \frac{30\sqrt{3}}{3} = 10√3

Entonces, la altura del árbol x+y = 5√3+10√3

= 15√3 metros

Pregunta 29: Al pie de una montaña, la elevación de su cima es de 45°, después de ascender 1000m hacia la montaña por una pendiente de 30° de inclinación, se encuentra que la elevación es de 60°. Encuentra la altura de la montaña.

Solución:

Supongamos que AB es una montaña de altura t+x.

c = 1000m

En △DFC,

sen 30° =\frac{x}{1000}

\frac{1}{2} = \frac{x}{1000}

x = \frac{1000}{2} = 500 metros

Y tan 30° =\frac{x}{y}

\frac{1}{\sqrt{3}} = \frac{500}{y}

y = 500√3m

Ahora, en △ABC

bronceado 45° =\frac{t+x}{y+z}

1 =\frac{t+500}{y+z}

500√3+z = t+500

500(√3-1)+z = t …………………..(1)

Ahora, en △ADE

bronceado 60° =\frac{t}{z}

√3 =\frac{t}{z}

t = √3z ………………….(2)

De (1) y (2), obtenemos

z = 500 m

t = 500√3m

Entonces, la altura de la montaña = t+x = 500√3 + 500 = 500(√3+1)m

Pregunta 30: Una persona observa que el ángulo de elevación del pico de una colina desde una estación es α. Camina c metros a lo largo de una pendiente inclinada en un ángulo β y encuentra que el ángulo de elevación del pico de la colina es γ. Demuestre que la altura del pico sobre el suelo es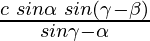\frac{c \hspace{0.1cm}sin \alpha \hspace{0.1cm}sin(\gamma-\beta)}{sin\gamma - \alpha}

Solución:

Supongamos que AB es un pico cuya altura sobre el suelo es t+x,

En △DFC,

sen β =\frac{x}{c}

x = c sen β ………………………..(1)

Y, tan β =\frac{x}{y}

y = \frac{x}{tan β} = \frac{c sin β}{tan β} = c cos β ………………………..(2)

Ahora, en △ADE

tan γ =\frac{t}{z}

z = t cot γ ………………………(3)

Ahora, en △ABC

bronceado α=\frac{t+x}{y+z}

t +x = tan α (y+z)

De (1), (2) y (3), obtenemos

t + c sen β = tan α (c cos β+t cot γ)

t + c sin β = c tan α cos β + t tan α cot γ

t – t tan α cot γ = c tan α cos β – c sin β

t(1 – tan α cot γ) = c (tan α cos β – sin β)

t(1 - \frac{sin α cos γ}{cos α sin γ}) = c (\frac{sin α cos β - cos α sin β}{cos α})\\ t(\frac{cos α sin γ-sin α cos γ}{cos α sin γ}) = c (\frac{sin (α-β)}{cos α})\\ t(\frac{sin(γ-α)}{cos α sin γ}) = c (\frac{sin (α-β)}{cos α})\\ t = c (\frac{sin (α-β)sin γ}{sin(γ-α)})

Ahora,

t+x = c (\frac{sin (α-β)sin γ}{sin(γ-α)}) + c sin β\\ = c (\frac{sin (α-β)sin γ}{sin(γ-α)} + sin β)\\ = c (\frac{sin (α-β)sin γ+sin(γ-α)sin β}{sin(γ-α)})\\ = c (\frac{sin γ(sin α cos β - cos α sin β)+sin β(sin γ cos α - cos γ sin α)}{sin(γ-α)})\\ = c (\frac{sin γ sin α cos β - sin γ cos α sin β + sin β sin γ cos α - sin β cos γ sin α}{sin(γ-α)})\\ = c (\frac{sin γ sin α cos β - sin β cos γ sin α}{sin(γ-α)})\\ = c (\frac{sin α (sin γ cos β - sin β cos γ)}{sin(γ-α)})\\ = c (\frac{sin α (sin(γ-β)}{sin(γ-α)})\\ = \frac{c sin α (sin(γ-β)}{sin(γ-α)}

Por lo tanto demostrado !!

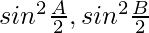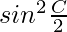Pregunta 31: Si los lados a, b y c de △ABC están en HP Demuestra que sin^2\frac{A}{2}, sin^2\frac{B}{2} y sin^2\frac{C}{2} están en HP

Solución:

Si los lados a, b y c de △ABC están en HP

Entonces, \frac{1}{a} , \frac{1}{b} y \frac{1}{c} están en AP

\frac{1}{b} - \frac{1}{a} = \frac{1}{c} - \frac{1}{b}\\ \frac{a-b}{ba} = \frac{b-c}{ca}

Según la regla del seno

\frac{a}{sin \hspace{0.1cm}A} = \frac{b}{sin \hspace{0.1cm}B} = \frac{c}{sin \hspace{0.1cm}C} = \lambda

\frac{sin \hspace{0.1cm}A-sin \hspace{0.1cm}B}{sin \hspace{0.1cm}Bsin \hspace{0.1cm}A} = \frac{sin \hspace{0.1cm}B-sin \hspace{0.1cm}C}{sin \hspace{0.1cm}Csin \hspace{0.1cm}B}

Usando la fórmula trigonométrica,

sen a – sen b = 2 sen (\frac{a-b}{2}) cos(\frac{a+b}{2})

\frac{2 sin (\frac{A-B}{2}) cos(\frac{A+B}{2})}{sin \hspace{0.1cm}A} = \frac{sin (\frac{B-C}{2}) cos(\frac{B+C}{2})}{sin \hspace{0.1cm}C}\\ \frac{sin (\frac{A-B}{2}) cos(\frac{\pi-C}{2})}{sin \hspace{0.1cm}A} = \frac{sin (\frac{B-C}{2}) cos(\frac{\pi-A}{2})}{sin \hspace{0.1cm}C}\\ \frac{sin (\frac{A-B}{2}) cos(\frac{\pi}{2}-\frac{C}{2})}{sin \hspace{0.1cm}A} = \frac{sin (\frac{B-C}{2}) cos(\frac{\pi}-\frac{A}{2})}{sin \hspace{0.1cm}C}\\ \frac{sin (\frac{A-B}{2}) sin(\frac{C}{2})}{2 sin(\frac{A}{2})cos(\frac{A}{2})} = \frac{cos(\frac{C}{2}) sin(\frac{A}{2})}{2 sin(\frac{C}{2})cos(\frac{C}{2})}\\ (sin (\frac{A-B}{2}) sin(\frac{C}{2}))(2 sin(\frac{C}{2})cos(\frac{C}{2})) = 2 sin(\frac{A}{2})sin(\frac{A}{2}) (cos(\frac{A}{2}) cos(\frac{A}{2}))\\ sin (\frac{A-B}{2}) sin^2(\frac{C}{2}) cos(\frac{C}{2}) = cos(\frac{C}{2}) sin^2(\frac{A}{2})cos(\frac{A}{2})\\ sin (\frac{A-B}{2}) sin^2(\frac{C}{2}) sin(\frac{A+B}{2}) = cos(\frac{C}{2}) sin^2(\frac{A}{2})sin(\frac{B+C}{2})\\ sin^2(\frac{C}{2})(sin^2(\frac{A}{2})-sin^2(\frac{B}{2}))= sin^2(\frac{A}{2})(sin^2(\frac{B}{2})-sin^2(\frac{C}{2}))\\ sin^2(\frac{C}{2}) sin^2(\frac{A}{2}) - sin^2(\frac{C}{2}) sin^2(\frac{B}{2}))= sin^2(\frac{A}{2}) sin^2(\frac{B}{2})-sin^2(\frac{A}{2}) sin^2(\frac{C}{2})

Dividido por sin^2\frac{A}{2} .sin^2\frac{B}{2}. sin^2\frac{C}{2} , obtenemos

\frac{1}{sin^2\frac{B}{2}} - \frac{1}{sin^2\frac{A}{2}} = \frac{1}{sin^2\frac{C}{2}} - \frac{1}{sin^2\frac{B}{2}}

Por lo tanto, sin^2\frac{A}{2}, sin^2\frac{B}{2} y sin^2\frac{C}{2} están en HP

Publicación traducida automáticamente

Artículo escrito por adi1212 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *