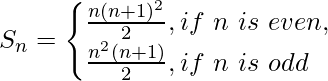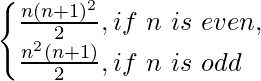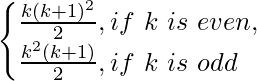Pregunta 33. Demuestra que n 11 /11 + n 5 /5 + n 3 /3 – 62/165n es cierto para todo n ∈ N.
Solución:
Sea, P(n) = n 11 /11 + n 5 /5 + n 3 /3 – 62/165n
Paso 1:
Ahora, comprobemos P(n) para n = 1.
Entonces, P(1) = 1/11 + 1/5 + 1/3 – 62/165 = 1
Entonces, P(1) es verdadero.
Paso 2:
Consideremos que P (n) es la verdadera para n = m,
Sea, P(m) = m 11 /11 + m 5 /5 + m 3 /3 – 62/165m
Entonces, m 11/11 + m 5/5 + m 3/3 – 62/165m = λ, donde λ ∈ N es un número entero positivo .
Paso 3:
Ahora, tenemos que demostrar que P(m + 1) es cierto.
P(m + 1) = (m + 1) 11 /11 + (m + 1) 5 /5 + (m + 1) 3 /3 – 62/165(m + 1)
= 1/11(m 11 + 11m 10 + 55m 9 + 165m 8 + 330m 7 + 462m 6 + 462m 5 + 330m 4 +
165m 3 + 55m 2 + 11m + 1) + 1/5(m 5 + 5m 4 + 10m 3 + 10m 2 + 5m + 1) +
1/3(m3 + 3m2 + 3m + 1) + 62/165(m + 1)
= λ + metro 6 + 3m 5 + 5m 4 + 5m 3 + 3m 2 + metro + metro 4 + 2m 3 + 2m 2 + metro + metro 2 + metro + metro + 1
Como λ es positivo, entonces es un entero positivo.
Entonces, P (n) es cierto para n = m + 1
es decir, P (n) es cierto para todo n ∈ N
Por lo tanto, por el principio de Inducción Matemática (PMI), P (n) es cierto para todo n ∈ N.
Pregunta 34. Demuestra que (1/2)tan(x/2) + (1/4)tan(x/4) +…..+ (1/2 n )tan(x/2 n ) = (1/ 2 n )cot(x/2 n ) – cotx para todo n ∈ N y 0< x < π/2.
Solución:
Sea, P(n) = (1/2)tan(x/2) + (1/4)tan(x/4) +…..+ (1/2 n )tan(x/2 n ) = ( 1/2 n )cot(x/2 n ) – cotx, para todo n ∈ N y 0< x < π/2.
Paso 1:
Ahora, comprobemos P(n) para n = 1.
IZQ = 1/2 tan(x/2)
RHS = (1/2)cot(x/2) – cuna(x) = 1/(2tan(x/2)) – 1 tan(x)
= 1/(2tan(x/2)) – 1/(2tan(x/2))/(1 – tan 2 (x/2))
= 1/(2tan(x/2)) – (1 – tan 2 (x/2))/(2tan(x/2))
=(1/2)bronceado(x/2)
Entonces, P(1) es verdadero.
Paso 2:
Consideremos que P (n) es la verdadera para n = m,
P(m) = (1/2)tan(x/2) + (1/4)tan(x/4) +…..+ (1/2 m )tan(x/2 m ) = (1/ 2 m )cuna(x/2 m ) – cunax
Paso 3:
Ahora, tenemos que demostrar que P(m + 1) es cierto.
P(m + 1) = (1/2)tan(x/2) + (1/4)tan(x/4) +…..+ (1/2 m )tan(x/2 m ) + ( 1/2 (m + 1) )tan(x/2 (m + 1) ) = (1/2 (m + 1) )cot(x/2 (m + 1) ) – cotx
Entonces, = (1/2 m )cot(x/2 m ) – cotx + (1/2 (m+1) )cot(x/2 (m+1) )
= (1/2 m )cot (x/2 m ) + (1/2 (m+1) )tan(x/2 (m+1) ) – cotx
= 1/(2 m tan(2x/2 (m+1) ) + (1/2 (m+1) )tan(x/2 (m+1) ) – cox
= [(1 – tan 2 (x/2 (m+1) ))/2 (m+1) .tan(x/2 (m+1) )] + (1/2 (m+1) )tan (x/2 (m+1) ) – cox
= (1/2 (m+1) )cota(x/2 (m+1) ) – cotax
Ahora,
(1/2)bronceado(x/2) + (1/4)bronceado(x/4)+…..+ (1/2 m )bronceado(x/2 m ) + (1/2 (m+1 ) )tan(x/2 (m+1) ) = (1/2 (m+1) )cot(x/2 (m+1) ) – cox
Entonces, P (n) es cierto para n = m + 1
es decir, P (n) es cierto para todo n ∈ N
Por lo tanto, por el principio de Inducción Matemática (PMI), P (n) es cierto para todo n ∈ N.
Pregunta 35. Demuestre que (1 – 1/2 2 )(1 – 1/3 2 )(1 – 1/4 2 )……(1 – 1/n 2 ) = (n + 1)/2n es cierto para todo n ∈ N.
Solución:
Sea, P(n) = (1 – 1/2 2 )(1 – 1/3 2 )(1 – 1/4 2 )……(1 – 1/n 2 ) = (n + 1)/2n
Paso 1:
Ahora, comprobemos P(n) para n = 2.
P(2) = 1 – 1/2 2 = (2 + 1)/2.2
o, 3/4 = 3/4
Entonces, P(2) es verdadero.
Paso 2:
Consideremos que P(n) es la verdadera para n = k, entonces, P(k) es
P(k) = (1 – 1/2 2 )(1 – 1/3 2 )(1 – 1/4 2 )……(1 – 1/k 2 ) = (k + 1)/2k
Paso 3:
Ahora, tenemos que demostrar que P(k + 1) es cierto. es decir
P(k + 1) = (1 – 1/2 2 )(1 – 1/3 2 )(1 – 1/4 2 )……(1 – 1/(k + 1) 2 ) = (k + 2 )/2k
Ahora, (1 – 1/2 2 )(1 – 1/3 2 )(1 – 1/4 2 )……(1 – 1/k 2 )(1 – 1/(k + 1) 2 )
Ahora, del paso 2, obtenemos
Entonces, (1 – 1/(k + 1) 2 )((k + 1)/2k)
o, ((k + 1)/2k)((k 2 + 1 + 2k – 1)/(k + 1) 2 )
o bien, k(k + 2)/2k(k + 1)
o, (k + 2)/2(k + 1)
Entonces, P (n) es cierto para n = k + 1
es decir, P (n) es cierto para todo n ∈ N
Por lo tanto, por el principio de Inducción Matemática (PMI), P (n) es cierto para todo n ∈ N.
Pregunta 36. Demuestra que (2n)!/2 2n (n!) 2 ≤ 1/√(3n + 1) es cierto para todo n ∈ N.
Solución:
Sea, P(n) = (2n)!/2 2n (n!) 2 ≤ 1/√(3n + 1)
Paso 1:
Ahora, comprobemos P(n) para n = 1.
P(1) = 1/2 ≤ 1/√3 + 1 = 1/2
Entonces, P(1) es verdadero.
Paso 2:
Consideremos que P (n) es la verdadera para n = m.
P(m) = (2m)!/2 2m (m!) 2 ≤ 1/√(3m + 1)
Paso 3:
Ahora, tenemos que demostrar que P(m + 1) es cierto. es decir
P(m + 1) = (2m + 2)!/2 2m+2 (m!) 2 ≤ 1/√(3m + 4)
Ahora,
P(m + 1) = ((2m + 1)(2m + 1)(2m)!)/(2m 2 .2 2 (m + 1) 2 (m!) 2 )
o, (2m + 2)!/2{2m + 2}((m + 1)!) 2 = ((2m)!/2 2m ) × (2m + 1)(m + 2)/2 2 (m + 1) 2
o, (2m + 2)!/2{2m + 2}((m + 1)!) 2 ≤ (2m + 1)/2(m + 1)√(3m + 1)
o, (2m + 2)!/2{2m + 2}((m + 1)!) 2 ≤ √((2m + 1) 2 /4(m + 1) 2 (3m + 1))
(2m + 2)!/2{2m + 2}((m + 1)!) 2 ≤ √((2m + 1) 2 /4(m + 1) 2 (3m + 1))
o, (2m + 2)!/2{2m + 2}((m + 1)!) 2 ≤ √(12m 3 + 28m 2 + 19m + 4)/(12m 3 + 28m 2 + 20m + 4)( 3 metros + 4)
ahora, (12m 3 + 28m 2 + 19m + 4)/(12m 3 + 28m 2 + 20m + 4) < 1
entonces, (2m + 2)!/2{2m + 2}((m + 1)!) 2 ≤ 1/√(3m + 4)
Entonces, P (n) es cierto para n = m + 1
es decir, P (n) es cierto para todo n ∈ N
Por lo tanto, por el principio de Inducción Matemática (PMI), P (n) es cierto para todo n ∈ N.
Pregunta 37. Demostrar que 1 + 1/4 + 1/9 + 1/16 + …..+ 1/n 2 < 2 – 1/n para todo n > 2, n ∈ N.
Solución:
Sea P(n) = 1 + 1/4 + 1/9 + 1/16 + …..+ 1/n 2 < 2 – 1/n para todo n > 2, n ∈ N
Paso 1:
Ahora, comprobemos P(n) para n = 2.
P(2) = 1/2 2 < 2 – 1/2
Entonces, P(1) es verdadero.
Paso 2:
Consideremos que P (n) es la verdadera para n = m.
P(m) = 1 + 1/4 + 1/9 + 1/16 +…..+ 1/m 2 < 2 – 1/m
Paso 3:
Ahora, tenemos que demostrar que P(m + 1) es cierto. es decir,
Del paso 2 tenemos, 1 + 1/4 + 1/9 + 1/16 +…..+ 1/m 2 < 2 – 1/m
Ahora, sumando 1/(m + 1) 2 a ambos lados, obtenemos
= 1 + 1/4 + 1/9 + 1/16 +…..+ 1/m 2 + 1/(m + 1) 2 < 2 – 1/m + 1/(m + 1) 2
o, (m + 1) 2 > m + 1
o bien, 1/(m + 1) 2 < 1/(m + 1)
o, 1/m – 1/(m + 1) 2 < 1/(m + 1)
Entonces, P(m + 1) < 2 – 1/(m + 1)
Entonces, P (n) es cierto para n = m + 1
es decir, P (n) es cierto para todo n ∈ N
Por lo tanto, por el principio de Inducción Matemática (PMI), P (n) es cierto para todo n ∈ N.
Pregunta 38. Demuestra que x 2n-1 + y 2n-1 es divisible por x + y.
Solución:
Sea P(n) x 2n-1 + y 2n-1
Paso 1:
Ahora, comprobemos P(n) para n = 1.
P(1) = x + y
Entonces, P(1) es divisible por x + y.
Entonces, P(1) es verdadera.
Paso 2:
Consideremos que P (n) es la verdadera para n = m.
P(m) = x 2m-1 + y 2m-1 = λ(x + y) ……….. (i)
Paso 3:
Ahora, tenemos que demostrar que P(m + 1) es cierto.
es decir, P(m + 1) = x 2m+1 + y 2m+1
= x2m +1 + y2m +1 – x2m -1 . y 2 + x 2m-1 . 2 años
= x2m -1 (x2 – y2 ) + y2 ( x2m -1 + y2m-1 )
= (x + y)(x 2m-1 (x – y) + λy 2 )
Entonces, P (n) es cierto para n = m + 1
es decir, P (n) es cierto para todo n ∈ N
Por lo tanto, por el principio de Inducción Matemática (PMI), P (n) es cierto para todo n ∈ N.
Pregunta 39. Demuestra que senx + sen3x + …+ sen(2n – 1)x = sen 2 nx/senx es cierto para todo n ∈ N.
Solución:
Sea, P(n) = senx + sen3x + …+ sen(2n – 1)x = sen 2 nx/senx
Paso 1:
Ahora, comprobemos P(n) para n = 1.
P(1) = sen x = sen 2 x / sen x = sen x
Entonces, P(1) es verdadera.
Paso 2:
Consideremos que P (n) es la verdadera para n = m.
P(m) = senx + sen3x + …+ sen(2m – 1)x = sen 2 mx/senx
Paso 3:
Ahora, tenemos que demostrar que P(m + 1) es cierto.
es decir,
P(m + 1) = senx + sen3x +…+ sen(2m – 1)x + sen(2m + 1)x = (sen 2 mx /senx) + sen(2m+1)x
ahora,
P(m + 1) = {(sen 2 mx + senx[sen(mx) + cos(m + 1)x + sen(m + 1)x + cos(mx)])}/senx
= {(sen 2 mx + 2senx.cosx.cos(mx) – sen 2 x.sen 2 mx + cos 2 mx.sen 2 x)}/senx
= {(sen 2 mx(1 – sen 2 x) + 2senx.cosx.cos(mx) + cos 2 mx.sen 2 x)}/senx
= {(sen 2 mx.cos 2 x + 2senx.cosx.cos(mx) + cos 2 mx.sen 2 x)}/senx
= {(sen(mx).cosx + cos(mx).senx) 2 }/senx
= {(sen(m + 1)x) 2 }/senx
Entonces, P (n) es cierto para n = m + 1
es decir, P (n) es cierto para todo n ∈ N
Por lo tanto, por el principio de Inducción Matemática (PMI), P (n) es cierto para todo n ∈ N.
Pregunta 40. Demuestra que ![Rendered by QuickLaTeX.com cosα + cos(α +β) +cos(α +2β)+....+cos(α +(n-1)β)=\frac{(cos[α +(\frac{n-1}{2})β] sin(\frac{nβ}{2}))}{sin(\frac{β}{2})}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4935bf6fbd50a85e1d662f1d5e55dec5_l3.png) es cierto para todo n ∈ N.
es cierto para todo n ∈ N.
Solución:
Sea, P(n) =
Paso 1:
Ahora, comprobemos P(n) para n = 1.
LHS = cos [α + (1 – 1)β] = cos α
lado derecho =
Entonces, P(1) es verdadero ya que LHS y RHS son iguales.
Paso 2:
Consideremos que P(n) es la verdadera para n = k.
P(k) =
Paso 3:
Ahora, tenemos que demostrar que P(k + 1) es cierto.
Entonces, sumando cos(α + kβ) a ambos lados de P(k), obtenemos
Ahora,
Entonces, P (n) es cierto para n = k + 1
es decir, P (n) es cierto para todo n ∈ N
Por lo tanto, por el principio de Inducción Matemática (PMI), P (n) es cierto para todo n ∈ N.
Pregunta 41. Demuestra que 1/(n+1) + 1/(n+2) +…..+ 1/2n > 13/24 para todos los números naturales, n > 1.
Solución:-
Sea,P(n) = 1/(n+1) + 1/(n+2) +…..+ 1/2n > 13/24
Paso 1:
Ahora, comprobemos P(n) para n = 2.
P(2) = 1/(2 + 1) + 1/(2 + 2) = 1/3 + 1/4 = 7/12 > 13/24
Entonces, P(2) es verdadero.
Paso 2:
Consideremos que P(n) es la verdadera para n = k, entonces, P(k) es
P(k) = 1/(k + 1) + 1/(k + 2) +…..+ 1/2k > 13/24
Paso 3:
Ahora, tenemos que demostrar que P(k + 1) es cierto. Cuando P(k) es verdadera.
Entonces, P(k + 1) = 1/(k + 2) + 1/(k + 3) +…..+ 1/2k + 1/2(k + 1)
Aquí, como LHS = RHS
Entonces, P (n) es cierto para n = k + 1
es decir, P (n) es cierto para todo n ∈ N
Por lo tanto, por el principio de Inducción Matemática (PMI), P (n) es cierto para todo n ∈ N.
Pregunta 42. Dado un 1 = 1/2(a 0 + A/a 0 ), un 2 = 1/2(a 1 + A/a 1 ) y un n+1 = 1/2(a n + A/ a n ), a, A > 0
Probar: 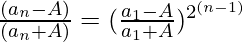
Solución:
Sea, P(n) =
Paso 1:
Ahora, comprobemos P(n) para n=1.
IZQ = (a 1 – √A) / (a 1 + √A)
lado derecho =
= (a 1 – √A) / (a 1 + √A)
Entonces, P(1) es verdadera.
Paso 2:
Consideremos que P(n) es la verdadera para n = k, entonces, P(k) es
Entonces, P(k) =
Paso 3:
Ahora, tenemos que demostrar que P(k + 1) es cierto. Cuando P(k) es verdadera.
Entonces, P(k + 1) = LHS = (a k+1 – √A) / (a k+1 + √A)
= (1/2(a k + A/a k ) – √A) / (1/2(a k + A/a k ) + √A)
= (1/2(a k 2 + A – 2a k √A)/a k ) / (1/2(a k 2 + A + 2a k √A)/a k )
= (a k+1 – √A) 2 / (a k+1 + √A) 2
=
![Rendered by QuickLaTeX.com [ [\frac{a_1 - √A}{a_1 + √A}]^{2^{k-1}}]^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4f248da419817252b03c73add237f2d2_l3.png)
=
aquí, como LHS = RHS
Entonces, P (n) es cierto para n = k + 1
es decir, P (n) es cierto para todo n ∈ N
Por lo tanto, por el principio de Inducción Matemática (PMI), P (n) es cierto para todo n ∈ N.
Pregunta 43. Sea P(n) el enunciado: 2 n ≥ 3n. Si P(r) es verdadera, entonces demuestre que P(r + 1) es verdadera. ¿Concluye que P(n) es verdadera para todo n ∈ N?.
Solución:
Sea P(n) = 2 n ≥ 3n
Paso 1:
Ahora, comprobemos P(n) para n = 1.
IZQ = 2
lado derecho = 3
Como LHS < RHS
Entonces, P(1) es verdadera.
Paso 2:
Consideremos que P (n) es la verdadera para n = r, entonces, P (r) es 2 r ≥ 3r
Paso 3:
Ahora, tenemos que demostrar que P(k + 1) es cierto. Cuando P(k) es verdadera.
Entonces, P(k + 1) = 2 r+1 = 2.2 r
Para, x > 3, 2x > x + 3
Entonces, 2.2 r > 2 r +3 para r > 1
o,2 r+1 > 2 r +3 para r > 1
o bien, 2 r+1 > 3r +3 para r > 1
o, 2 r+1 > 3(r + 1) para r >1
Entonces, P (n) es cierto para n = r + 1
es decir, P (n) es cierto para todo n ∈ N
Por lo tanto, por el principio de Inducción Matemática (PMI), P (n) es cierto para todo n ∈ N.
Pregunta 44. Demostrar por el principio de Inducción Matemática que la suma Sn de los n términos de la serie 1 2 + 2 × 2 2 + 3 2 + 2 × 4 2 + 5 2 + 2 × 6 2 + 7 2 +… es dada por
Solución:
Sea, P(n) = S n = 1 2 + 2 × 2 2 + 3 2 + 2 × 4 2 + 5 2 + 2 × 6 2 + 7 2 +… =
Paso 1:
Ahora, comprobemos P(n) para n = 1.
LHS = 1 = RHS
Entonces, P(1) es verdadera.
Paso 2:
Consideremos que P(n) es la verdadera para n = k, entonces, P(k) es
P(k) = 1 2 + 2,2 2 + 3 2 + 2,4 2 + 5 2 =
Paso 3:
Ahora, tenemos que demostrar que P(k + 1) es cierto. Cuando P(k) es verdadera.
Caso 1: cuando k es impar, entonces (k + 1) es par
P(k + 1) = LHS = 1 2 + 2.2 2 + 3 2 + 2.4 2 + 5 2 …. k 2 + 2.(k + 1) 2
= k 2 (k + 1)/2 + 2.(k + 1) 2
= {(k 2 (k + 1) + 4(k + 1) 2 )}/2
= (k + 1)(k + 2) 2 /2
ahora, RHS = (k + 1)(k + 1 + 1 ) 2/2
= (k + 1)(k + 2) 2 /2
Entonces, es cierto para n = k + 1, cuando k es impar.
Caso 2: cuando k es par, entonces (k + 1) es impar
P(k + 1) = LHS = 1 2 + 2.2 2 + 3 2 + 2.4 2 + 5 2 ….+ 2. k 2 + (k + 1) 2
= k(k + 1) 2 /2 + (k + 1) 2
= (k(k + 1) 2 + 2.(k + 1) 2 )/2
= (k + 1) 2 (k + 2)/2
RHS = (k + 1) 2 (k + 1 + 1)/2
= (k + 1) 2 (k + 2)/2
ahora, LHS = RHS.
Entonces, es cierto para n=k+1, cuando k es par.
Entonces, P (n) es cierto para n = k + 1
es decir, P (n) es cierto para todo n ∈ N
Por lo tanto, por el principio de Inducción Matemática (PMI), P (n) es cierto para todo n ∈ N.
Pregunta 45. Demostrar que el número de subconjuntos de un conjunto que contiene n elementos distintos es 2 n para todo n ∈ N.
Solución:
Sea, P(n): El número de subconjuntos de un conjunto que contiene n elementos distintos = 2 n , para todo n ∈ N.
Paso 1:
Ahora, comprobemos P(n) para n = 1.
LHS = As, los subconjuntos del conjunto que contiene solo 1 elemento son:
Φ y el propio conjunto
es decir, el número de subconjuntos de un conjunto que contiene solo el elemento = 2
lado derecho = 2 1 = 2
ahora, LHS = RHS
Entonces, P(1) es verdadera.
Paso 2:
Consideremos que P (n) es la verdadera para n = k,
Entonces, P(k) es El número de subconjuntos de un conjunto que contiene k elementos distintos = 2 k
Paso 3:
Ahora, tenemos que demostrar que P(k + 1) es cierto. Cuando P(k) es verdadera.
P(k + 1) = Sea A = {a 1 , a 2 , a 3 , a 4 ,..…, a k , b} de modo que A tiene (k + 1) elementos.
Ahora, el subconjunto t de A se puede dividir en dos conjuntos tales que
Primero contiene subconjuntos de A que no tienen b en ellos y
El segundo contiene subconjuntos de A que tienen b en ellos.
Entonces, Primera colección: {}, {a 1 }, {a 1 , a 2 }, {a 1 , a 2 , a 3 },…,{a 1 , a 2 , a 3 , a 4 ,…, a k } y
y la segunda colección: {b}, {a 1 , b}, {a 1 , a 2 , b}, {a 1 , a 2 , a 3 , b},…,{a 1 , a 2 , a 3 , a 4 ,…, a k , b}
Se puede ver claramente que:
El número de subconjuntos de A en la primera colección.
= El número de subconjuntos del conjunto con k elementos, es decir, {a 1 , a 2 , a 3 , a 4 ,…, a k } = 2k
Además, se deduce que la segunda colección debe tener
el mismo número de los subconjuntos que el del primero = 2 k
Así que el número total de subconjuntos de A = 2 k + 2 k = 2 k+1
Entonces, P (n) es cierto para n = k + 1
es decir, P (n) es cierto para todo n ∈ N
Por lo tanto, por el principio de Inducción Matemática (PMI), P (n) es cierto para todo n ∈ N.
Pregunta 46. Una sucesión a 1 , a 2 , a 3 ,….. se define haciendo a 1 = 3 y a k = 7a k-1 para todos los números naturales k ≥ 2. Demostrar que a n = 3.7 n- 1 para todo n ∈ N.
Solución:
Sea P(n) un n = 3.7 n-1 para todo n ∈ N
Paso 1:
Ahora, comprobemos P(n) para n = 1.
entonces, a 1 = 3.7 1-1 = 3
Entonces, P(1) es verdadera.
Paso 2:
Consideremos que P (n) es la verdadera para n = k,
P(k) = un k = 3,7 k-1
Paso 3:
Ahora, tenemos que demostrar que P(k + 1) es cierto. Cuando P(k) es verdadera.
P(k + 1) = un k+1 = 7.un k
= 7.3.7 k-1
= 3,7 k-1+1
= 3,7 (k+1)-1
Entonces, P (n) es cierto para n = k + 1
es decir, P (n) es cierto para todo n ∈ N
Por lo tanto, por el principio de Inducción Matemática (PMI), P (n) es cierto para todo n ∈ N.
Pregunta 47. Una sucesión x 1 , x 2 , x 3 ,….. se define haciendo x 1 = 2 y x k = x k-1 /k para todos los números naturales k, k ≥ 2. Demostrar que x n = 2/n! para todo n ∈ N.
Solución:
Sea P(n) x n = 2/n! para todo n ∈ N.
Paso 1:
Ahora, comprobemos P(n) para n = 1.
P(1) = x1 = 2/1! = 2
Entonces, P(1) es verdadera.
Paso 2:
Consideremos que P (n) es la verdadera para n = k,
P(k) = xk = 2/k!
Paso 3:
Ahora, tenemos que demostrar que P(k + 1) es cierto. Cuando P(k) es verdadera.
entonces, x k+1 = 2/(k + 1)!
o bien, 2/(k + 1).k!
o bien, 2/(k + 1)!
Entonces, P (n) es cierto para n = k + 1
es decir, P (n) es cierto para todo n ∈ N
Por lo tanto, por el principio de Inducción Matemática (PMI), P (n) es cierto para todo n ∈ N.
Pregunta 48. Una secuencia x 0 , x 1 , x 2 , x 3 , ……. se define haciendo x 0 = 5 y x k = 4 + x k -1 para todo número natural k. Demuestre que x n = 5 + 4 n para todo n ∈ N usando inducción matemática.
Solución:-
Sea, P(n) = x n = 5 + 4n para todo n ∈ N
Paso 1:
Ahora, comprobemos P(n) para n = 0.
P(0) = 5 + 4(0) = 5
Entonces, P(0) es verdadera.
Paso 2:
Consideremos que P (n) es la verdadera para n = k,
P(k) = x k = 5 + 4k
Paso 3:
Ahora, tenemos que demostrar que P(k + 1) es cierto. Cuando P(k) es verdadera.
entonces, P(k + 1) = x k+1 = 4 + x k+1 -1
= 4 + xk
= 4 + 5 + 4k
= 5 + 4(k + 1)
Entonces, P (n) es cierto para n = k + 1
es decir, P (n) es cierto para todo n ∈ N
Por lo tanto, por el principio de Inducción Matemática (PMI), P (n) es cierto para todo n ∈ N.
Pregunta 49. Usando el principio de inducción matemática, demuestre que
√n < 1/√1 + 1/√2+ 1/√3 +…..+1/√n para todos los números naturales n ≥2.
Solución:
Sea, P(n) = √n < 1/√1 + 1/√2+ 1/√3 +…..+1/√n para todo n ≥ 2.
Paso 1:
Ahora, comprobemos P(n) para n=2.
P(2) = √2 < 1 + 1/√2
o bien, 1,41 < 1 + 0,707 = 1,707
Entonces, P(2) es verdadero.
Paso 2:
Consideremos que P (n) es la verdadera para n = k,
P(k) = √k < 1/√1 + 1/√2+ 1/√3 +…..+1/√k
Paso 3:
Ahora, tenemos que demostrar que P(k+1) es cierto. Cuando P(k) es verdadera.
Ahora, LHS = √(k + 1)
Ahora, RHS = 1/√1 + 1/√2+ 1/√3 +…..+1/√k + 1/√(k + 1)
o, k/√{(k + 1)} < √k
o, k + 1/√{(k + 1)} – 1/√(k + 1) < √k
o, √(k + 1) – 1/√(k + 1)< √k
o, √(k + 1) < √k + 1/√(k + 1)
entonces, LHS < RHS.
Entonces, P (n) es cierto para n = k + 1
es decir, P (n) es cierto para todo n ≥ 2
Por lo tanto, por el principio de Inducción Matemática (PMI), P (n) es cierto para todo n ≥ 2.
Pregunta 50. La ley distributiva del álgebra establece que para todos los números reales, a 1 y a 2 , tenemos c (a 1 + a 2 ) = ca 1 + ca 2 . Utilice esta ley y la inducción matemática para demostrar que, para todos los números naturales, n ≥ 2, si c, a 1 , a 2 ,…,an son números reales cualesquiera, entonces c (a 1 +a 2 +…+a n ) = ca 1 +ca 2 +…+ca n .
Solución:
Sea, P(n) = c (a 1 +a 2 +…+a n ) = ca 1 +ca 2 +…+ca n , para todos los números naturales, n ≥ 2.
Paso 1:
Ahora, comprobemos P(n) para n=2.
IZQ = c(a 1 + a 2 )
RHS = aproximadamente 1 + aproximadamente 2
Entonces, P(2) es verdadero.
Paso 2:
Consideremos que P (n) es la verdadera para n = k,
P(k) = c(a 1 +a 2 +…+a k ) = ca 1 +ca 2 ++ …+ca k
Paso 3:
Ahora, tenemos que demostrar que P(k+1) es cierto. Cuando P(k) es verdadera.
IZQ = c(a 1 +a 2 +…+a k + a k+1 )
= c[(a 1 +a 2 +…+a k ) + a k+1 ]
= c(a 1 +a 2 +…+a k ) + ca k+1
= ca 1 +ca 2 +…+ca k + ca k+1
= lado derecho
Entonces, P (n) es cierto para n = k + 1
es decir, P (n) es cierto para todo n ≥ 2
Por lo tanto, por el principio de Inducción Matemática (PMI), P (n) es cierto para todo n ≥ 2.
Publicación traducida automáticamente
Artículo escrito por manjeetks007 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
![Rendered by QuickLaTeX.com \frac{(cos[α +(\frac{1-1}{2})β] sin(\frac{β}{2}))}{sin(\frac{β}{2})} = cosα](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-daee18569012d4d10b0dcff4bfcbe4b8_l3.png)
![Rendered by QuickLaTeX.com cosα + cos(α +β) +cos(α +2β)+....+cos(α +(k-1)β)=\frac{(cos[α +(\frac{k-1}{2})β] sin(\frac{kβ}{2}))}{sin(\frac{β}{2})}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-255b21e23014cb2917690a6798e28509_l3.png)
![Rendered by QuickLaTeX.com P(k+1)= cosα + cos(α +β) +cos(α +2β)+....+cos(α +(k-1)β) +cos(α +kβ)=\frac{(cos[α +(\frac{k-1}{2})β] sin(\frac{kβ}{2}))}{sin(\frac{β}{2})}+cos(α +kβ)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6677f9b7a0a0801716594bda085130fb_l3.png)
![Rendered by QuickLaTeX.com =\frac{(cos[α +(\frac{k-1}{2})β] sin(\frac{kβ}{2})+cos(α +kβ)sin(\frac{β}{2})}{sin(\frac{β}{2})}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ad0291220e4fb7f6242f6918ac6406ff_l3.png)
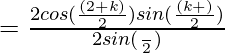
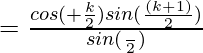
![Rendered by QuickLaTeX.com RHS= \frac{(cos[α +(\frac{kβ}{2})] sin(\frac{(k+1)β}{2}))}{sin(\frac{β}{2})}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bd7567160f9bc20f71a5877f5cfb1c3e_l3.png)