Pregunta 1. Encuentra la raíz cuadrada de los siguientes números complejos.
(i) – 5 + 12i
(ii) -7 – 24i
(iii) 1 – yo
(iv) – 8 – 6i
(v) 8 – 15i
(v) ![]()
(vii) ![]()
(viii) 4i
(ix) -yo
Solución:
Si b > 0, ![Rendered by QuickLaTeX.com \sqrt{a+ib}=\pm\left[\left(\frac{a+\sqrt{a^2+b^2}}{2}\right)^{\frac{1}{2}}+i\left(\frac{-a+\sqrt{a^2+b^2}}{2}\right)^{\frac{1}{2}}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-62b69331f0dfb4b958dfe4c45f2b5134_l3.png)
Si b < 0, ![Rendered by QuickLaTeX.com \sqrt{a+ib}=\pm\left[\left(\frac{a+\sqrt{a^2+b^2}}{2}\right)^{\frac{1}{2}}-i\left(\frac{-a+\sqrt{a^2+b^2}}{2}\right)^{\frac{1}{2}}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c1560bee11e70aa9b9555382da36939f_l3.png)
(i) – 5 + 12i
Dado:
– 5 + 12i
Sabemos, Z = a + ib
Asi que,
Aquí, b > 0
Simplifiquemos ahora,
∴ La raíz cuadrada de (– 5 + 12i) es ±[2 + 3i]
(ii) -7 – 24i
Dado:
-7-24i
Sabemos, Z = -7 – 24i
Asi que,
Aquí, b < 0
Simplifiquemos ahora,
∴ La raíz cuadrada de (-7 – 24i) es ± [3 – 4i]
(iii) 1 – yo
Dado:
1 – yo
Sabemos, Z = (1 – i)
Asi que,
Aquí, b < 0
Simplifiquemos ahora,
∴ La raíz cuadrada de (1 – i) es ±
(iv) -8 -6i
Dado:
-8 -6i
Sabemos, Z = -8 -6i
Entonces,
= -8 -6i
Aquí, b < 0
Simplifiquemos ahora,
∴ La raíz cuadrada de (-8 -6i) es ± [1 – 3i]
(v) 8 – 15i
Dado:
8-15i
Sabemos, Z = 8 – 15i
Entonces,
= 8 – 15i
Aquí, b < 0
Simplifiquemos ahora,
∴ La raíz cuadrada de (8 – 15i) es ±
(v) ![]()
Dado:
Sabemos, Z =
Asi que,
= -11 – 60i
Aquí, b < 0
Simplifiquemos ahora,
∴ La raíz cuadrada de (
) es ± (5 – 6i)
(vii) ![]()
Dado:
Sabemos, Z =
Asi que,
Aquí, b > 0
Simplifiquemos ahora,
∴ La raíz cuadrada de
es ±
(viii) 4i
Dado:
4i
Sabemos, Z = 4i
Entonces,
= 4i
Aquí, b > 0
Simplifiquemos ahora,
∴ La raíz cuadrada de 4i es ±
(ix) –i
Dado:
-i
Sabemos, Z = -i
Entonces,
= -i
Aquí, b < 0
Simplifiquemos ahora,
∴ La raíz cuadrada de –i es ±
Publicación traducida automáticamente
Artículo escrito por codersgram9 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
![Rendered by QuickLaTeX.com \sqrt{-5+12i}=\pm\left[\left(\frac{-5+\sqrt{(-5)^2+12^2}}{2}\right)^{\frac{1}{2}}+i\left(\frac{5+\sqrt{(-5)^2+12^2}}{2}\right)^{\frac{1}{2}}\right]\ \ \ [Since\ b>0]\\ =\pm\left[\left(\frac{-5+\sqrt{25+144}}{2}\right)^{\frac{1}{2}}+i\left(\frac{5+\sqrt{25+144}}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\left(\frac{-5+\sqrt{169}}{2}\right)^{\frac{1}{2}}+i\left(\frac{5+\sqrt{169}}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\left(\frac{-5+13}{2}\right)^{\frac{1}{2}}+i\left(\frac{5+13}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\left(\frac{8}{2}\right)^{\frac{1}{2}}+i\left(\frac{18}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[4^{\frac{1}{2}}+i9^{\frac{1}{2}}\right]\\ =\pm[2+3i]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-733a1fc9776eaaf5799422101c38b884_l3.png)
![Rendered by QuickLaTeX.com \sqrt{-7-24i}=\pm\left[\left(\frac{-7+\sqrt{(-7)^2+(-24)^2}}{2}\right)^{\frac{1}{2}}-i\left(\frac{7+\sqrt{(-7)^2+(-24)^2}}{2}\right)^{\frac{1}{2}}\right]\ \ \ [Since\ b<0]\\ =\pm\left[\left(\frac{-7+\sqrt{49+576}}{2}\right)^{\frac{1}{2}}-i\left(\frac{7+\sqrt{49+576}}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\left(\frac{-7+\sqrt{625}}{2}\right)^{\frac{1}{2}}-i\left(\frac{7+\sqrt{625}}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\left(\frac{-7+25}{2}\right)^{\frac{1}{2}}-i\left(\frac{7+25}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\left(\frac{18}{2}\right)^{\frac{1}{2}}-i\left(\frac{32}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[9^{\frac{1}{2}}-i16^{\frac{1}{2}}\right]\\ =\pm[3-4i]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0a20a25850a2b47665bf5d80c51b81d9_l3.png)
![Rendered by QuickLaTeX.com \sqrt{1-i}=\pm\left[\left(\frac{1+\sqrt{(1)^2+(-1)^2}}{2}\right)^{\frac{1}{2}}-i\left(\frac{-1+\sqrt{(1)^2+(-1)^2}}{2}\right)^{\frac{1}{2}}\right]\ \ \ [Since\ b<0]\\ =\pm\left[\left(\frac{1+\sqrt{1+1}}{2}\right)^{\frac{1}{2}}-i\left(\frac{-1+\sqrt{1+1}}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\left(\frac{1+\sqrt{2}}{2}\right)^{\frac{1}{2}}-i\left(\frac{-1+\sqrt{2}}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\left(\sqrt{\frac{\sqrt2+1}{2}}\right)-i\left(\sqrt{\frac{\sqrt2-1}{2}}\right)\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6b56f6ff6e111d3a4bbec4ccf98b8596_l3.png)
![Rendered by QuickLaTeX.com \pm\left[\left(\sqrt{\frac{\sqrt2+1}{2}}\right)-i\left(\sqrt{\frac{\sqrt2-1}{2}}\right)\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9ce6d301b4412e1e8529793e869c4000_l3.png)
![Rendered by QuickLaTeX.com \sqrt{-8-6i}=\pm\left[\left(\frac{-8+\sqrt{(-8)^2+(-6)^2}}{2}\right)^{\frac{1}{2}}-i\left(\frac{8+\sqrt{(-8)^2+(-6)^2}}{2}\right)^{\frac{1}{2}}\right]\ \ \ [Since\ b<0]\\ =\pm\left[\left(\frac{-8+\sqrt{64+36}}{2}\right)^{\frac{1}{2}}-i\left(\frac{8+\sqrt{64+36}}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\left(\frac{-8+\sqrt{100}}{2}\right)^{\frac{1}{2}}-i\left(\frac{8+\sqrt{100}}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\left(\frac{-8+10}{2}\right)^{\frac{1}{2}}-i\left(\frac{8+10}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\left(\frac{2}{2}\right)^{\frac{1}{2}}-i\left(\frac{10}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[1^{\frac{1}{2}}-i9^{\frac{1}{2}}\right]\\ =\pm[1-3i]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-058683232443b4679b1b6971684ee108_l3.png)
![Rendered by QuickLaTeX.com \sqrt{8-15i}=\pm\left[\left(\frac{8+\sqrt{(8)^2+(-15)^2}}{2}\right)^{\frac{1}{2}}-i\left(\frac{-8+\sqrt{(8)^2+(-15)^2}}{2}\right)^{\frac{1}{2}}\right]\ \ \ [Since\ b<0]\\ =\pm\left[\left(\frac{8+\sqrt{64+225}}{2}\right)^{\frac{1}{2}}-i\left(\frac{-8+\sqrt{64+225}}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\left(\frac{8+\sqrt{289}}{2}\right)^{\frac{1}{2}}-i\left(\frac{-8+\sqrt{289}}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\left(\frac{8+17}{2}\right)^{\frac{1}{2}}-i\left(\frac{-8+17}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\left(\frac{25}{2}\right)^{\frac{1}{2}}-i\left(\frac{9}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\frac{5}{\sqrt2}-\frac{13}{\sqrt2}\right]\\ =\pm\frac{1}{\sqrt2}(5-3i)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b33ae047c6c1833328d76ef87f5d5aae_l3.png)
![Rendered by QuickLaTeX.com \sqrt{-11-60i}=\pm\left[\left(\frac{-11+\sqrt{(-11)^2+(-60)^2}}{2}\right)^{\frac{1}{2}}-i\left(\frac{11+\sqrt{(-11)^2+(60)^2}}{2}\right)^{\frac{1}{2}}\right]\ \ \ [Since\ b<0]\\ =\pm\left[\left(\frac{-11+\sqrt{121+3600}}{2}\right)^{\frac{1}{2}}-i\left(\frac{11+\sqrt{121+3600}}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\left(\frac{-11+\sqrt{3721}}{2}\right)^{\frac{1}{2}}-i\left(\frac{11+\sqrt{3721}}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\left(\frac{-11+61}{2}\right)^{\frac{1}{2}}-i\left(\frac{11+61}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\left(\frac{50}{2}\right)^{\frac{1}{2}}-i\left(\frac{72}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[25^{\frac{1}{2}-i36^{\frac{1}{2}}}\right]\\ =\pm(5-6i)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5dc0992649e3368b8782c206085f73ac_l3.png)
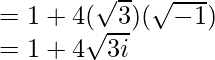
![Rendered by QuickLaTeX.com \sqrt{1+4\sqrt3i}=\pm\left[\left(\frac{1+\sqrt{(1)^2+(4\sqrt3)^2}}{2}\right)^{\frac{1}{2}}+i\left(\frac{-1+\sqrt{1^2+(4\sqrt3)^2}}{2}\right)^{\frac{1}{2}}\right]\ \ \ [Since\ b>0]\\ =\pm\left[\left(\frac{1+\sqrt{1+48}}{2}\right)^{\frac{1}{2}}+i\left(\frac{-1+\sqrt{1+48}}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\left(\frac{1+\sqrt{49}}{2}\right)^{\frac{1}{2}}+i\left(\frac{-1+\sqrt{49}}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\left(\frac{1+7}{2}\right)^{\frac{1}{2}}+i\left(\frac{-1+7}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\left(\frac{8}{2}\right)^{\frac{1}{2}}+i\left(\frac{6}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[4^{\frac{1}{2}}+i3^{\frac{1}{2}}\right]\\ =\pm[2+\sqrt3i]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-444f8b48b222cc6601d25e6aa06064ee_l3.png)
![Rendered by QuickLaTeX.com \sqrt{4i}=\pm\left[\left(\frac{0+\sqrt{(0)^2+(4)^2}}{2}\right)^{\frac{1}{2}}+i\left(\frac{0+\sqrt{0^2+(4)^2}}{2}\right)^{\frac{1}{2}}\right]\ \ \ [Since\ b>0]\\ =\pm\left[\left(\frac{0+\sqrt{0+16}}{2}\right)^{\frac{1}{2}}+i\left(\frac{0+\sqrt{0+16}}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\left(\frac{0+\sqrt{16}}{2}\right)^{\frac{1}{2}}+i\left(\frac{0+\sqrt{16}}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\left(\frac{0+4}{2}\right)^{\frac{1}{2}}+i\left(\frac{0+4}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\left(\frac{4}{2}\right)^{\frac{1}{2}}+i\left(\frac{4}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[2^{\frac{1}{2}}+i2^{\frac{1}{2}}\right]\\ =\pm[\sqrt2+\sqrt2i]\\ =\pm\sqrt2(1+i)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ca1fc56494ceb45f3ba31b84fb97ea7d_l3.png)
![Rendered by QuickLaTeX.com \sqrt{-i}=\pm\left[\left(\frac{0+\sqrt{0^2+(-1)^2}}{2}\right)^{\frac{1}{2}}-i\left(\frac{0+\sqrt{0^2+(-1)^2}}{2}\right)^{\frac{1}{2}}\right]\ \ \ [Since\ b<0]\\ =\pm\left[\left(\frac{0+\sqrt{0+1}}{2}\right)^{\frac{1}{2}}-i\left(\frac{0+\sqrt{0+1}}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\left(\frac{0+\sqrt{1}}{2}\right)^{\frac{1}{2}}-i\left(\frac{0+\sqrt{1}}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\left(\frac{0+1}{2}\right)^{\frac{1}{2}}-i\left(\frac{0+1}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\left(\frac{1}{2}\right)^{\frac{1}{2}}-i\left(\frac{1}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\frac{1}{\sqrt2}-\frac{i}{\sqrt2}\right]\\ =\pm\frac{1}{\sqrt2}(1-i)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4ececf7d8dda29280607c675f20c3109_l3.png)