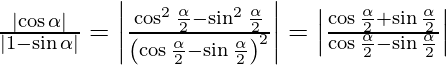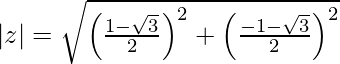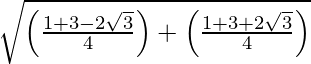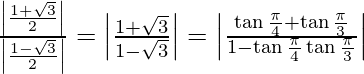Pregunta 1. Encuentre el módulo y el argumento de los siguientes números complejos y, por lo tanto, exprese cada uno de ellos en la forma polar:
(yo) 1 + yo
(ii) √3 + yo
(iii) 1 – yo
(iv) (1 – i)/(1 + i)
(v) 1/(1 + yo)
(vi) (1 + 2i)/(1 – 3i)
(vii) sen 120 o – i cos 120 o
(viii) –16/(1 + i√3)
La forma polar de un número complejo Z = x + iy viene dada por Z = |Z| (cos θ + i sen θ) donde,
Módulo de número complejo, |Z| = √( x2 + y2 )
Argumento del número complejo, θ = arg (Z) = tan –1 (y/x)
(yo) 1 + yo
Solución:
Nos dan, Z = 1 + i, por lo que x = 1 y y = 1.
|Z| = √(1 2 + 1 2 ) = √2
θ = bronceado -1 (1/1) = bronceado -1 1
Como x > 0 y y > 0, Z se encuentra en el primer cuadrante y el valor de θ es 0 ≤ θ ≤ π/2.
Entonces, θ = π/4 y Z = √2 (cos (π/4) + i sin (π/4))
Por lo tanto, la forma polar de (1 + i) es √2 (cos (π/4) + i sin (π/4)).
(ii) √3 + yo
Solución:
Nos dan, Z = √3 + i, entonces x = √3 y y = 1.
|Z| = √((√3) 2 + 1 2 ) = 2
θ = bronceado -1 (1/√3)
Como x > 0 y y > 0, Z se encuentra en el primer cuadrante y el valor de θ es 0 ≤ θ ≤ π/2.
Entonces, θ = π/6 y Z = 2 (cos (π/6) + i sin (π/6))
Por lo tanto, la forma polar de (√3 + i) es √2 (cos (π/6) + i sin (π/6)).
(iii) 1 – yo
Solución:
Nos dan, Z = 1 – i, entonces x = 1 y y = –1.
|Z| = √(1) 2 + (–1) 2 ) = √2
θ = bronceado -1 (1/1) = bronceado -1 1
Como x > 0 y y < 0, Z se encuentra en el cuarto cuadrante y el valor de θ es –π/2 ≤ θ ≤ 0.
Entonces, θ = – π/4 y,
Z = √2 (cos (–π/4) + i sin (–π/4))
= √2 (cos (π/4) – i sen (π/4))
Por lo tanto, la forma polar de (1 – i) es √2 (cos (π/4) – i sin (π/4)).
(iv) (1 – i)/(1 + i)
Solución:
Nos dan, Z = (1 – i)/(1 + i).
Multiplicando y dividiendo por (1 – i), obtenemos,
Z =
=
=
=
= 0 – yo
Entonces x = 0, y = –1 y |Z| = √(0 2 + (–1) 2 ) = 1
θ = bronceado -1 (1/0)
Como x ≥ 0 y y < 0, Z se encuentra en el cuarto cuadrante y el valor de θ es –π/2 ≤ θ ≤ 0.
Entonces, θ = –π/2 y,
Z = 1 (cos (–π/2) + i sin (–π/2))
= cos (π/2) – i sen (π/2)
Por lo tanto, la forma polar de (1 – i)/(1 + i) es cos (π/2) – i sin (π/2).
(v) 1/(1 + yo)
Solución:
Nos dan, Z = (1 – i)/(1 + i).
Multiplicando y dividiendo por (1 – i), obtenemos,
Z =
=
=
=
= 1/2 – i/2
Entonces x = 1/2, y = –1/2 y |Z| = √((1/2) 2 + (–1/2) 2 ) = √(2/4) = 1/√2
θ = bronceado -1 ((1/2)/(1/2)) = bronceado –1 1
Como x > 0 y y < 0, Z se encuentra en el cuarto cuadrante y el valor de θ es –π/2 ≤ θ ≤ 0.
Entonces, θ = –π/4 y,
Z = 1/√2 (cos (-π/4) + i sin (-π/4))
= 1/√2 (cos (π/4) – i sin (π/4))
Por lo tanto, la forma polar de 1/(1 + i) es 1/√2 (cos (π/4) – i sin (π/4)).
(vi) (1 + 2i)/(1 – 3i)
Solución:
Nos dan, Z = (1 + 2i)/(1 – 3i).
Multiplicando y dividiendo por (1 + 3i), obtenemos,
Z =
=
=
=
= –1/2 + i/2
Entonces x = –1/2, y = 1/2 y |Z| = √((–1/2) 2 + (1/2) 2 ) = √(2/4) = 1/√2
θ = tan-1 ((1/2)/(1/2)) = tan –1 1
Como x < 0 y y > 0, Z se encuentra en el segundo cuadrante y el valor de θ es π/2 ≤ θ ≤ π.
Entonces, θ = 3π/4 y Z = 1/√2 (cos (3π/4) + i sin (3π/4))
Por lo tanto, la forma polar de (1 + 2i)/(1 – 3i) es 1/√2 (cos (3π/4) + i sin (3π/4)).
(vii) sen 120 o – i cos 120 o
Solución:
Nos dan, Z = sen 120 o – i cos 120 o
= √3/2 – yo (–1/2)
= √3/2 + yo (1/2)
Entonces x = √3/2, y = 1/2 y |Z| = √((√3/2) 2 + (1/2) 2 ) = √(3/4 + 1/4) = 1
θ = bronceado -1 ((1/2)/(√3/2)) = bronceado -1 (1/√3)
Como x > 0 y y > 0, Z se encuentra en el primer cuadrante y el valor de θ es 0 ≤ θ ≤ π/2.
Entonces, θ = π/6 y Z = 1 (cos (π/6) + i sin (π/6))
Por lo tanto, la forma polar de √3/2 + i (1/2) es 1 (cos (π/6) + i sin (π/6)).
(viii) -16/(1 + i√3)
Nos dan, Z = –16/(1 + i√3).
Multiplicando y dividiendo por (1 – i√3), obtenemos,
Z =
=
=
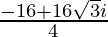
= –4 + 4√3 yo
Entonces x = –4, y = 4/√3 y |Z| = √((–4) 2 + (4√3) 2 ) = √(16 + 48) = 8
θ = bronceado -1 (4√3/4) = bronceado -1 (√3)
Como x < 0 y y > 0, Z se encuentra en el segundo cuadrante y el valor de θ es π/2 ≤ θ ≤ π.
Entonces, θ = 2π/3 y Z = 8 (cos (2π/3) + i sin (2π/3))
Por lo tanto, la forma polar de -16 / (1 + i√3) es 8 (cos (2π/3) + i sin (2π/3)).
Pregunta 2. Escribe (i 25 ) 3 en forma polar.
Solución:
Se nos da,
Z = (i 25 ) 3
= yo 75
= (yo 2 ) 37 . i
= (–1) 37 . i
= – yo
= 0 – yo
Entonces x = 0, y = –1 y,
|Z| = √( x2 + y2 )
= √(0 2 + (–1) 2 )
= 1
θ = tan –1 (|y| / |x|)
= bronceado –1 (1 / 0)
Dado que x ≥ 0 y y < 0, Z se encuentra en el cuarto cuadrante y el valor de θ es π/2 ≤ θ ≤ 0. Entonces, θ = –π/2.
Z = 1 (cos (–π/2) + i sin (–π/2))
= 1 (cos (π/2) – i sen (π/2))
Por lo tanto, la forma polar de (i 25 ) 3 es 1 (cos (π/2) – i sin (π/2)).
Pregunta 3. Exprese los siguientes números complejos en la forma r (cos θ + i sen θ ):
(i) 1 + i tan α
(ii) tan α – i
(iii) 1 − sen α + i cos α
(iv) ![]()
Solución:
(i) 1 + i tan α
Nos dan 1 + i tan α, entonces x = 1 y y = tan α.
También sabemos que tan α es una función periódica con período π.
Entonces α está en el intervalo [0, π/2) ∪ (π/2, π].
Caso 1: Si α ∈ [0, π/2)
|Z| = r = √(1 2 + tan 2 α)
= √( segundo 2 α)
= segundo α
θ = tan -1 (tan α/1)
= tan -1 (tan α)
= α
Entonces, Z = sec α (cos α + i sin α)
Por lo tanto, la forma polar es sec α (cos α + i sin α).
Caso 2: α ∈ (π/2, π]
|Z| = r = √(1 2 + tan 2 α)
= √( segundo 2 α)
= – seg α
θ = tan -1 (tan α/1)
= tan -1 (tan α)
= –π + α
Entonces, Z = –seg α (cos (α – π) + i sin (α – π))
Por lo tanto, la forma polar es –sec α (cos (α – π) + i sin (α – π)).
(ii) tan α – i
Nos dan tan α – i, entonces x = tan α e y = –1.
También sabemos que tan α es una función periódica con período π.
Entonces α está en el intervalo [0, π/2) ∪ (π/2, π].
Caso 1: Si α ∈ [0, π/2)
|Z| = r = √(tan 2 α + 1)
= √( segundo 2 α)
= segundo α
θ = tan -1 (1/tan α)
= tan -1 (cuna α)
= α – π/2
Entonces, Z = sec α (cos (α – π/2) + i sin (α – π/2))
Por lo tanto, la forma polar es sec α (cos (α – π/2) + i sin (α – π/2)).
Caso 2: α ∈ (π/2, π]
|Z| = r = √(tan 2 α + 1)
= √( segundo 2 α)
= – seg α
θ = tan -1 (1/tan α)
= tan -1 (cuna α)
= π/2 + α
Entonces, Z = –seg α (cos (π/2 + α) + i sin (π/2 + α))
Por lo tanto, la forma polar es –sec α (cos (π/2 + α) + i sin (π/2 + α)).
(iii) 1 − sen α + i cos α
Sea z = 1 − sen α + i cos α
Como las funciones seno y coseno son funciones periódicas con periodo 2π, tomemos α en [0, 2π].
Ahora, z = 1 − sen α + i cos α
Sea θ un ángulo agudo dado por,
tan θ =
tan θ =
tan θ =
Caso 1: Cuando 0 ≤ α < π/2
En este caso, tenemos,
|z| = √2(cos α/2 – sen α/2)
También,
tan θ = |tan (π/4 + α/2)| = bronceado (π/4 + α/2)
θ = π/4 + α/2
Claramente, z se encuentra en el primer cuadrante. Por lo tanto, arg(z) = π/4 + α/2
Por tanto, la forma polar de z es √2(cos α/2 – sen α/2){cos (π/4 + α/2) + i sen (π/4 + α/2)}.
Caso 2: Cuando π/2 < α < 3π/2
En este caso, tenemos,
|z| = |√2(cos α/2 – sen α/2)| = -√2(cos α/2 – sen α/2)
Y, tan θ = |tan (π/4 + α/2)| = -tan (π/4 + α/2) = tan {π – (π/4 + α/2)} = tan (α/2 – 3π/4)
θ = 3π/4 + α/2
Claramente, z se encuentra en el cuarto cuadrante. Por lo tanto, arg(z) = -θ = 3π/4 + α/2 = α/2 – 3π/4
Por lo tanto, la forma polar de z es -√2(cos α/2 – sin α/2){cos (α/2 – sin 3π/4) + i sin (α/2 – sin 3π/4)}..
Caso 3: Cuando 3π/2 < α < 2π
En este caso, tenemos,
|z| = |√2(cos α/2 – sen α/2)| = -√2(cos α/2 – sen α/2)
Y tan θ = |tan (π/4 + α/2)| = bronceado (π/4 + α/2) = – bronceado {π – (π/4 + α/2)} = bronceado (α/2 – 3π/4)
θ = α/2 – 3π/4
Claramente, z se encuentra en el primer cuadrante. Por lo tanto, arg(z) = θ = α/2 – 3π/4
Por lo tanto, la forma polar de z es -√2(cos α/2 – sen α/2){cos (α/2 – sen 3π/4) + i sen (α/2 – sen 3π/4)}.
(iv)
Sea z =
=
=
=
=
=
=
Ahora, z =
=
=
= √2
Sea θ un ángulo agudo dado por tan θ =
tan θ =
bronceado θ = | bronceado (π/4 + π/3)| = |tan 7π/12|
θ = 7π/12
Claramente, z se encuentra en el cuarto cuadrante. Por lo tanto, arg(z) = -7π/12
Por lo tanto, la forma polar de z es √2(cos 7π/12 – sen 7π/12).
Pregunta 4. Si z 1 y z 2 son dos números complejos tales que |z 1 | = |z 2 | y arg (z 1 ) + arg (z 2 ) = π, luego demuestre que 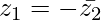 .
.
Solución:
Nos dan |z 1 | = |z 2 | y arg (z 1 ) + arg (z 2 ) = π. Supongamos que arg (z 1 ) = θ, luego arg (z 2 ) = π – θ.
Sabemos que z = |z| (cos θ + i sen θ)
z2 = | z2 | (cos (π – θ) + i sen (π – θ))
= |z 2 | (–cos θ + i sen θ)
= – |z 2 | (cos θ – i sen θ)
El conjugado de z 2 ,
= – |z 2 | (cos θ + i sen θ)
Ahora LHS = z 1 = |z 1 | (cos θ + i sen θ)
= |z 2 | (cos θ + i sen θ)
= – [– |z 2 | (cos θ + i sen θ)]
=
= lado derecho
Por lo tanto probado.
Pregunta 5. Si z 1 , z 2 y z 3 , z 4 son dos pares de números complejos conjugados, probar que arg (z 1 /z 4 ) + arg (z 2 /z 3 ) = 0
Solución:
Se nos da,
LHS = argumento (z 1 /z 4 ) + argumento (z 2 /z 3 )
= argumento (z 1 ) − argumento (z 4 ) + argumento (z 2 ) − argumento (z 3 )
= [argumento (z 1 ) + argumento (z 2 )] − [argumento (z 3 ) + argumento (z 4 )]
=
= 0 − 0
= 0
= lado derecho
Por lo tanto probado.
Pregunta 6. Exprese sen π /5 + i (1 – cos π /5) en forma polar.
Solución:
Se nos da,
Z = sen π/5 + i (1 – cos π/5)
= 2 sen π/10 cos π/10 + i (2 sen 2 π/10)
= 2 sen π/10 (cos π/10 + i sen π/10)
Sabemos que la forma polar viene dada por r (cos θ + i sen θ).
Por tanto, la forma polar de la expresión dada es 2 sen π/10 (cos π/10 + i sen π/10).
Publicación traducida automáticamente
Artículo escrito por gurjotloveparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA