Clase 11 Soluciones RD Sharma – Capítulo 15 Inecuaciones lineales – Ejercicio 15.3

Pregunta 1. Resuelve 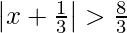$\izquierda | x + \frac{1}{3} \right | > \frac{8}{3}$

Solución:

Usando la propiedad del operador módulo, sabemos

|x| > a ⇒ x < -a o x > a

Por lo tanto, $\izquierda (x + \frac{1}{3} \derecha) < \frac{-8}{3}$ o $\izquierda (x + \frac{1}{3} \derecha) > \frac{8}{3}$

⇒ x < $\frac{-8}{3} - \frac{1}{3}$ o x > $\frac{8}{3} - \frac{1}{3}$

⇒ x < -3 o x > $\frac{7}{3}$

Por lo tanto, podemos concluir que x se encuentra en el rango ( -∞, -3) ∪ ( $\frac{7}{3}$ ,∞ )

Pregunta 2. Resolver | 4 – x | + 1 < 3

Solución:

tenemos, | 4 – x | + 1 < 3

⇒ | 4 – x | < 2

Usando la propiedad del operador módulo, sabemos

|x| < un ⇒ -a < x < un

⇒ -2 < 4 – x < 2

⇒ -6 < -x < -2

⇒ 6 > x > 2

⇒ 2 < x < 6

Por lo tanto, podemos concluir que x se encuentra en el rango (2, 6)

Pregunta 3. Resuelve 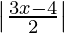$\izquierda | \frac{3x - 4}{2} \right |$ ≤ $\frac{5}{12}$

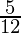
Solución:

Usando la propiedad del operador módulo, sabemos

|x| ≤ un ⇒ -a ≤ x ≤ un

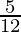
⇒ – $\frac{5}{12}$ ≤ $\frac{3x - 4}{2}$ ≤ $\frac{5}{12}$

⇒ – $\frac{5}{6}$ ≤ 3x – 4 ≤ $\frac{5}{6}$

⇒ – $\frac{5}{6}$ + 4 ≤ 3x ≤ $\frac{5}{6}$ + 4

⇒ $\frac{19}{6}$ ≤ 3x ≤ $\frac{29}{6}$

⇒ $\frac{19}{18}$ ≤ X ≤ $\frac{29}{18}$

Por lo tanto, podemos concluir que x se encuentra en el rango [ $\frac{19}{18}$ , $\frac{29}{18}$ ]

Pregunta 4. Resolver 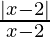$\frac{|x - 2|}{x - 2}$ > 0

Solución:

Usando la propiedad del operador módulo, tenemos

| x-2 | = x-2 cuando x ≥ 2 o 2-x cuando x < 2

ya que, $\frac{|x-2|}{x-2}$ > 0 para x > 2

Por lo tanto, podemos concluir que x se encuentra en el rango ( 2, ∞)

Pregunta 5. Resuelve 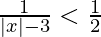$\frac{1}{|x|-3} < \frac{1}{2}$

Solución:

Se nos da, $\frac{1}{|x|-3} < \frac{1}{2}$

⇒ $\frac{1}{|x|-3} - \frac{1}{2}$ < 0

⇒ $\frac{2 - (|x|-3)}{2(|x|-3)}$ < 0

⇒ $\frac{2 - |x|+ 3}{|x|-3}$ < 0

⇒ $\frac{5 - |x|}{|x|-3}$ < 0

Ahora tenemos dos casos:

Caso 1: Cuando x ≥ 0, entonces |x| = x

$\frac{5-x}{x-3}$ < 0

⇒ (5 – x < 0 y x – 3 > 0) o ( 5 – x > 0 y x – 3 < 0)

⇒ (x > 5 y x > 3) o ( x < 5 y x < 3)

⇒ x > 5 y x < 3

Por lo tanto, podemos concluir, del caso 1, que x está en el rango [ 0,3) U (5,∞)

Caso 2: Cuando x ≤ 0 entonces |x| = -x

$\frac{5+x}{-x-3}$ < 0

⇒ $\frac{x+5}{x+3}$ > 0

⇒ (x + 5 > 0 y x + 3 > 0) o (x + 5 <0 y x + 3 < 0)

⇒ ( x > -5 y x > -3 ) o ( x < -5 y x < -3 )

⇒ x > -3 o x < -5

Por lo tanto, podemos concluir, del caso 2, que x está en el rango [ -∞, -5) U (-3,0)

Ahora, tomando la unión de los dos casos anteriores, podemos concluir que x se encuentra en el rango (-∞, -5) U (-3,3) U (5, ∞)

Pregunta 6. Resuelve 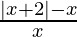$\frac{|x + 2| - x}{x}$ < 2

Solución:

Tenemos $\frac{|x + 2| - x}{x}$ < 2

⇒ $\frac{|x + 2| - x}{x}$ – 2 < 0

⇒ $\frac{|x + 2| - x -2x}{x}$ < 0

⇒ $\frac{|x + 2| - 3x}{x}$ < 0

Ahora tenemos dos casos:

Caso 1: Cuando x ≥ -2, entonces |x+2| =x+2,

$\frac{x + 2 - 3x}{x}$ < 0

⇒ $\frac{2-2x}{x}$ < 0

⇒ $\frac{-2(x-1)}{x}$ < 0

⇒ $\frac{x-1}{x}$ > 0

⇒ (x – 1 > 0 y x > 0) o (x – 1 < 0 y x < 0)

⇒ (x > 1 y x > 0) o (x < 1 y x < 0)

⇒ x > 1 o x < 0

Por lo tanto, podemos concluir, del caso 1, que x está en el rango [ -2,0) U (1,∞)

Caso 1: Cuando x ≤ -2, entonces |x+2| = -(x+2),

$\frac{-(x + 2) - 3x}{x}$ < 0

⇒ $\frac{-x-2-3x}{x}$ < 0

⇒ $\frac{-2(2x+1)}{x}$ < 0

⇒ $\frac{2x+1}{x}$ > 0

⇒ (2x -+ 1 > 0 y x > 0) o ( 2x + 1 < 0 y x < 0)

⇒ (x > -1/2 y x > 0) o (x < -1/2 y x < 0)

⇒ x > 0 o x < -1/2

Por lo tanto, podemos concluir, del caso 2, que x está en el rango ( -∞,-2 ] U (0,∞)

Ahora, tomando la unión de los dos casos anteriores, podemos concluir que x se encuentra en el rango [ -2,0 ) U (1,∞) U (-∞, -2] U ( 0, ∞) es decir, x pertenece a (- ∞,0) U (1,∞)

Pregunta 7. Resuelve 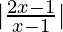$|\frac{2x-1}{x-1}|$ > 2

Solución:

Tenemos $|\frac{2x-1}{x-1}|$ > 2

⇒ $|\frac{2x-1}{x-1}|$ – 2 > 0

⇒ $\frac{2x-1}{x-1}$ > 0 o $\frac{2x-1}{x-1}$ +2 < 0

⇒ $\frac{1}{x-1}$ > 0 o $\frac{4x-3}{x-1}$ < 0

⇒ x-1 >0 o $\frac{4x-3}{x-1}$ < 0

⇒ x-1 > 0 o [ (4x-3 > 0 y x-1 < 0) o ( 4x-3 < 0 y x-1 > 0) ]

⇒ x > 1 o [ (x > 3/4 y x < 1) o ( x < 3/4 y x > 1) ]

⇒ x > 1 o [ 3/4 < x < 1 o ∅]

⇒ 3/4 < x < 1 o x > 1

Por lo tanto, podemos concluir que x se encuentra en el rango ( 3/4, 1) U (1, ∞ )

Pregunta 8. Resuelve |x-1| + |x-2| + |x-3| ≥ 6

Solución:

Tenemos, |x-1| + |x-2| + |x-3| ≥ 6 ———————sea esta la ecuación (1)

como, | x-1 | = ( x-1, cuando x ≥ 1 y 1-x cuando x < 1 )

del mismo modo, | x-2 | = ( x-2, cuando x ≥ 2 y 2-x cuando x < 2 )

y | x-3 | = ( x-3, cuando x ≥ 3 y 3-x cuando x < 3 )

Ahora tenemos cuatro casos:

Caso 1: Cuando x < 1

1 – x + 2 – x + 3 – x ≥ 6

⇒ 6 -3x ≥ 6

⇒ x ≤ 0

Entonces, vemos que x está en el rango (-∞,0]

Caso 2: cuando 1 ≤ x < 2

x – 1 + 2 – x + 3 – x ≥ 6

⇒ 4 – x ≥ 6

⇒ x ≤ -2

usando el caso 2, vemos que x no tiene valores entonces x ∈ ∅

Caso 3: cuando 2 ≤ x < 3

x – 1 + x – 2 + 3 – x ≥ 6

⇒ x ≥ 6

usando el caso 3, vemos que x no tiene valores entonces x ∈ ∅

Caso 4: cuando x ≥ 3

x-1 + x-2 + x-3 ≥ 6

⇒ 3x – 6 ≥ 6

⇒ x ≥ 4

usando el caso 4, vemos que x no tiene valores entonces x ∈ [ 4, ∞ )

Combinando todos los casos, sabemos que x está en el rango ( -∞, 0 ] U [ 4, ∞)

Pregunta 9. Resuelve 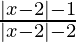$\frac{|x-2|-1}{|x-2|-2}$ ≤ 0

Solución:

Tenemos, $\frac{|x-2|-1}{|x-2|-2}$ ≤ 0

Caso 1: cuando x ≥ 2, entonces | x-2 | = x – 2

$\frac{x-2-1}{x-2-2}$ ≤ 0

⇒ $\frac{x-3}{x-4}$ ≤ 0

⇒ ( x – 3 ≤ 0 y x – 4 > 0 ) o ( x – 3 ≥ 0 y x – 4 < 0)

⇒ ( x ≤ 3 y x > 4 ) o ( x ≥ 3 y x < 4)

⇒ ∅ o ( 3 ≤ x < 4)

⇒ 3 ≤ x < 4

usando el caso 1, vemos que x está en el rango [3, 4]

Caso 2: cuando x ≤ 2, entonces | x-2| = 2 – x,

$\frac{2-x-1}{2-x-2}$ ≤ 0

⇒ $\frac{1-x}{-x}$ ≤ 0

⇒ $\frac{x-1}{x}$ ≤ 0

⇒ ( x – 1 ≤ 0 y x > 0 ) o ( x – 1 ≥ 0 y x< 0)

⇒ ( x ≤ 1 y x > 0 ) o ( x ≥ 1 y x< 0)

⇒ ( 0 < x ≤ 1) o ∅

⇒ 0 < x ≤ 1

usando el caso 2, vemos que x está en el rango (0, 1]

Combinando todos los casos, sabemos que x está en el rango ( 0, 1 ] U [ 3, 4)

Pregunta 10. Resuelve 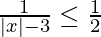$\frac{1}{|x|-3} \leq \frac{1}{2}$

Solución:

Tenemos, $\frac{1}{|x|-3} \leq \frac{1}{2}$

⇒ $\frac{1}{|x|-3} - \frac{1}{2}$ ≤ 0

⇒ $\frac{2 - (|x-3|)}{2(|x-3|)}$ ≤ 0

⇒ $\frac{5 - |x|}{|x|-3}$ ≤ 0

Caso 1: cuando x ≥ 0 entonces |x| = x

⇒ $\frac{5-x}{x-3}$ ≤ 0

⇒ ( 5 – x ≤ 0 y x – 3 > 0 ) o ( 5 – x ≥ 0 y x – 3 < 0)

⇒ ( x ≥ 5 y x > 3 ) o ( x ≤ 5 y x < 3)

⇒ x ≥ 5 o x < 3

usando el caso 1, vemos que x está en el rango ( 0, 3 ) U [5, ∞ )

Caso 2: cuando x < 0 entonces |x| = -x

⇒ $\frac{5+x}{-x-3}$ ≤ 0

⇒ $\frac{x+5}{x+3}$ ≥ 0

⇒ ( x + 5 > 0 y x + 3 > 0 ) o ( x + 5 < 0 y x + 3 < 0)

⇒ ( x > -5 y x > -3 ) o ( x < -5 y x < -3)

⇒ x > -3 o x < -5

usando el caso 2, vemos que x está en el rango ( -∞, -5 ) U (-3, ∞ )

Combinando ambos casos, sabemos que x está en el rango ( -∞, -5 ) U (-3, ∞ ) U ( 0, 3 ) U [5, ∞ )

Pregunta 11. Resuelve |x + 1| + |x| > 3

Solución:

Tenemos, |x + 1| + |x| > 3

⇒ |x + 1| = ( x + 1 cuando x ≥ -1 y -(x + 1) cuando x < -1 )

del mismo modo, |x| = (x cuando x ≥ 0 y -x cuando x < 0)

Caso 1: Cuando x < -1

|x + 1| + |x| > 3

⇒ – (x+1) -x > 3

⇒ -2x -1 > 3

⇒ x < -2

usando el caso `1, vemos que x está en el rango ( -∞, -2 )

Caso 2: Cuando -1 ≤ x < 0

|x + 1| + |x| > 3

⇒ (x+1) + x > 3

⇒ 2x > 2

⇒ x > 1

usando el caso `2, vemos que x está en el rango ( 1, ∞ )

Combinando ambos casos, sabemos que x está en el rango ( -∞, -2 ) U ( 1, ∞ )

Pregunta 12. Resuelve 1 ≤ |x – 2| ≤ 3

Solución:

Tenemos, 1 ≤ |x – 2| ≤ 3

Caso 1: |x – 2| ≥ 1

⇒ ((x – 2) ≤ -1 o (x-2) ≥ 1)

⇒ ( x ≤ 1 o x ≥ 3)

usando el caso `1, vemos que x está en el rango ( -∞,1 ] U [3,∞)

Caso 2: |x – 2| ≤ 3

⇒ (-3 ≤ (x-2) ≤ 3)

⇒ (-1 ≤ x ≤ 5)

usando el caso `2, vemos que x está en el rango [-1, 5]

Combinando ambos casos, sabemos que x se encuentra en el rango [-1, 1] U [3, 5]

Pregunta 13. Resuelve |3-4x| ≥ 9

Solución:

Tenemos, |3-4x| ≥ 9

por lo tanto, usando la propiedad del módulo sabemos, |x| ≥ un ⇒ x ≤ -a o x ≥ un

⇒ (3-4x) ≤ -9 o (3-4x) ≥ 9

⇒ -4x ≤ -12 o -4x ≥ 6

⇒ x ≥ 3 o x ≤ -3/2

Por lo tanto, podemos concluir que x se encuentra en el rango ( -∞, -3/2] U [ 3, ∞ )

Publicación traducida automáticamente

Artículo escrito por saurabh48782 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1. Resuelve

Pregunta 2. Resolver | 4 – x | + 1 < 3

Pregunta 3. Resuelve ≤

Pregunta 4. Resolver > 0

Pregunta 5. Resuelve

Pregunta 6. Resuelve < 2

Pregunta 7. Resuelve > 2

Pregunta 8. Resuelve |x-1| + |x-2| + |x-3| ≥ 6

Pregunta 9. Resuelve ≤ 0

Pregunta 10. Resuelve

Pregunta 11. Resuelve |x + 1| + |x| > 3

Pregunta 12. Resuelve 1 ≤ |x – 2| ≤ 3

Pregunta 13. Resuelve |3-4x| ≥ 9

Deja una respuesta Cancelar la respuesta

Pregunta 1. Resuelve $\izquierda | x + \frac{1}{3} \right | > \frac{8}{3}$

Pregunta 3. Resuelve $\izquierda | \frac{3x - 4}{2} \right |$ ≤ $\frac{5}{12}$

Pregunta 4. Resolver $\frac{|x - 2|}{x - 2}$ > 0

Pregunta 5. Resuelve $\frac{1}{|x|-3} < \frac{1}{2}$

Pregunta 6. Resuelve $\frac{|x + 2| - x}{x}$ < 2

Pregunta 7. Resuelve $|\frac{2x-1}{x-1}|$ > 2

Pregunta 9. Resuelve $\frac{|x-2|-1}{|x-2|-2}$ ≤ 0

Pregunta 10. Resuelve $\frac{1}{|x|-3} \leq \frac{1}{2}$