Clase 11 Soluciones RD Sharma – Capítulo 15 Inecuaciones lineales – Ejercicio 15.1

Pregunta 15. Resuelve: 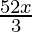$\frac{5−2x}{3}$ < $\frac{x}{6}$ − 5 en R.

Solución:

Dado: $\frac{5−2x}{3}$ < $\frac{x}{6}$ − 5

⇒ $\frac{5−2x}{3}$ < $\frac{x−30}{6}$

⇒ 6(5−2x) < 3(x−30)

⇒ 30 − 12x < 3x − 90

⇒ 15x > 120

⇒ x > 8

Así, el conjunto solución es (8, ∞).

Pregunta 16. Resuelve: 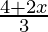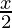$\frac{4+2x}{3}$ ≥ $\frac{x}{2}$ − 3.

Solución:

Dado: $\frac{4+2x}{3}$ ≥ $\frac{x}{2}$ − 3.

⇒ $\frac{4+2x}{3}$ ≥ $\frac{x−6}{2}$

⇒ 2(4+2x) ≥ 3(x−60)

⇒ 8 + 4x ≥ 3x − 180

⇒ x ≥ −26

Por tanto, el conjunto solución es [−26, ∞).

Pregunta 17. Resuelve: $\frac{2x+3}{5}$ − 2 < $\frac{3(x−2)}{5}$ .

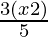Solución:

Dado: $\frac{2x+3}{5}$ − 2 < $\frac{3(x-2)}{5}$

⇒ $\frac{2x+3−10}{5}$ < $\frac{3x−6}{5}$

⇒ 2x + 3 − 10 < 3x − 6

⇒ x > −1

Por tanto, el conjunto solución es (−1, ∞).

Pregunta 18. Resuelve: x−2 ≤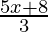 $\frac{5x+8}{3}$

Solución:

Dado: x−2 ≤ $\frac{5x+8}{3}$

⇒ 3(x−2) ≤ 5x+8

⇒ 3x − 6 ≤ 5x + 8

⇒ 2x ≥ −14

⇒ x ≥ −7

Por tanto, el conjunto solución es [−7, ∞).

Pregunta 19. Resuelve: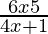 $\frac{6x−5}{4x+1}$ < 0.

Solución:

Dado: $\frac{6x−5}{4x+1}$ < 0.

Caso I: Cuando 6x − 5 > 0 y 4x +1 < 0

⇒ x > 5/6 y x < −1/4, lo cual es claramente imposible.

Caso II: Cuando 6x − 5 < 0 y 4x +1 > 0

⇒ x < 5/6 y x > −1/4

Por lo tanto, el conjunto solución es (−1/4, 5/6).

Pregunta 20. Resuelve: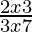 $\frac{2x−3}{3x−7}$ > 0.

Solución:

Dado: $\frac{2x−3}{3x−7}$ > 0.

Caso I: Cuando 2x−3 > 0 y 3x−7 > 0

⇒ x > 3/2 y x > 7/3

⇒ x > 7/3 ….(a)

Caso II: Cuando 2x−3 < 0 y 3x−7 < 0

⇒ x < 3/2 y x < 7/3

⇒ x < 3/2 ….(b)

De (a) y (b), obtenemos:

El conjunto solución es (− ∞, 3/2)∪ (7/3, ∞).

Pregunta 21. Resuelve: 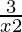$\frac{3}{x−2}$ < 1.

Solución:

Dado: $\frac{3}{x−2}$ < 1

⇒ $\frac{3}{x−2}$ −1 < 0

⇒ $\frac{3−x+2}{x−2}$ < 0

⇒ $\frac{x−5}{x−2}$ > 0

Caso I: Cuando x−5 > 0 y x−2 > 0

⇒ x > 5 y x > 2

⇒ x > 5 ….(a)

Caso II: Cuando x−5 < 0 y x−2 < 0

⇒ x < 5 y x < 2

⇒ x < 2 ….(b)

De (a) y (b), obtenemos:

El conjunto solución es (− ∞, 2)∪ (5, ∞).

Pregunta 22. Resuelve: $\frac{1}{x−1}$ ≤ 2.

Solución:

Dado: $\frac{1}{x−1}$ ≤ 2

⇒ $\frac{1}{x−1}$ − 2 ≤ 0

⇒ $\frac{1−2x+2}{x−1}$ ≤ 0

⇒ $\frac{3−2x}{x−1}$ ≤ 0

Caso I: Cuando 3−2x ≥ 0 y x−1 < 0

⇒ x ≥ 3/2 y x < 1

⇒ x < 1 …..(a)

Caso II: 3−2x ≤ 0 y x−1 > 0

⇒ x ≥ 3/2 y x > 1

⇒ x ≥ 3/2 ….(b)

De (a) y (b), obtenemos:

El conjunto solución es ( − ∞, 1)∪ (3/2, ∞).

Pregunta 23. Resuelve: $\frac{4x+3}{2x−5}$ < 6

Solución:

Dado: $\frac{4x+3}{2x−5}$ < 6

⇒ $\frac{4x+3}{2x−5}$ −6 < 0

⇒ $\frac{4x+3−12x+30}{2x−5}$ < 0

⇒ $\frac{8x−33}{2x−5}$ < 0

Caso I: Cuando 8x−33 > 0 y 2x−5 > 0

⇒ x > 33/8 y x > 5/2

⇒ x > 33/8 ….(a)

Caso II: Cuando 8x−33 < 0 y 2x−5 < 0

⇒ x < 33/8 y x < 5/2

⇒ x < 5/2 ….(b)

De (a) y (b), obtenemos:

El conjunto solución es (− ∞, 5/2)∪ (33/8, ∞).

Pregunta 24. Resuelve: $\frac{5x−6}{x+6}$ < 1.

Solución:

Dado: $\frac{5x−6}{x+6}$ < 1

⇒ $\frac{5x−6}{x+6}$ − 1 < 0

⇒ $\frac{5x−6−x−6}{x+6}$ < 0

⇒ $\frac{4x−12}{x+6}$ < 0

Caso I: Cuando 4x−12 > 0 y x+6 < 0

⇒ x > −3 y x < −6, lo que claramente no es posible.

Caso II: Cuando 4x−12 < 0 y x+6 > 0

⇒ x < −3 y x > −6

El conjunto solución es (− 3, 6).

Pregunta 25. Resuelve: 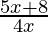$\frac{5x+8}{4−x}$ < 2.

Solución:

Dado: $\frac{5x+8}{4−x}$ < 2

⇒ $\frac{5x+8}{4−x}$ − 2 < 0

⇒ $\frac{5x+8−8+2x}{4−x}$ < 0

⇒ $\frac{7x}{4−x}$ < 0

Caso I: Cuando 7x > 0 y 4−x < 0

⇒ x > 0 y x > 4

⇒ x > 4 ….(a)

Caso II: Cuando 7x < 0 y 4−x > 0

⇒ x < 0 y x > 4

⇒ x < 0 ….(b)

De (a) y (b), obtenemos:

El conjunto solución es (− ∞, 0)∪ (4, ∞).

Pregunta 26. Resuelve: 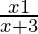$\frac{x−1}{x+3}$ > 2.

Solución:

Dado: $\frac{x−1}{x+3}$ > 2.

⇒ $\frac{x−1}{x+3}$ − 2 > 0

⇒ $\frac{x−1−2x−6}{x+3}$ > 0

⇒ $\frac{x+7}{x+3}$ < 0

Caso I: Cuando x+7 > 0 y x+3 < 0

⇒ x > −7 y x < −3

Caso II: Cuando x+7 < 0 y x+3 > 0

⇒ x < −7 y x > −3, lo que claramente no es posible.

El conjunto solución es (−7, −3).

Pregunta 27. Resuelve: $\frac{7x−5}{8x+3}$ > 4.

Solución:

Dado: $\frac{7x−5}{8x+3}$ > 4

⇒ $\frac{7x−5}{8x+3}$ − 4 > 0

⇒ $\frac{7x−5−32x−12}{8x+3}$ > 0

⇒ $\frac{−25x−17}{8x+3}$ > 0

⇒ $\frac{25x+17}{8x+3}$ < 0

Caso I: Cuando 25x+17 > 0 y 8x+3 < 0

⇒ x > −17/25 y x < −3/8

Caso II: Cuando 25x+17 < 0 y 8x+3 > 0

⇒ x < −17/25 y x > −3/8, lo que claramente no es posible.

Por lo tanto, el conjunto solución es (−17/25, −3/8).

Pregunta 28. Resuelve: 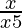$\frac{x}{x−5}$ > 1/2.

Solución:

Dado: $\frac{x}{x−5}$ > 1/2.

⇒ $\frac{x}{x−5}$ − 1/2 > 0

⇒ $\frac{x+5}{2x−10}$ > 0

Caso I: Cuando x+5 > 0 y 2x−10 > 0

⇒ x > −5 y x > 5

⇒ x > 5 ….(a)

Caso II: Cuando x+5 < 0 y 2x−10 < 0

⇒ x < −5 y x < 5

⇒ x < −5 ….(b)

De (a) y (b), obtenemos:

El conjunto solución es (− ∞, −5)∪ (5, ∞).

Publicación traducida automáticamente

Artículo escrito por prabhjotkushparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 11 Soluciones RD Sharma – Capítulo 15 Inecuaciones lineales – Ejercicio 15.1 | conjunto 2

Pregunta 15. Resuelve: $\frac{5−2x}{3}$ < $\frac{x}{6}$ − 5 en R.

Pregunta 16. Resuelve: $\frac{4+2x}{3}$ ≥ $\frac{x}{2}$ − 3.

Pregunta 17. Resuelve: $\frac{2x+3}{5}$ − 2 < $\frac{3(x−2)}{5}$ .

Pregunta 18. Resuelve: x−2 ≤ $\frac{5x+8}{3}$

Pregunta 19. Resuelve: $\frac{6x−5}{4x+1}$ < 0.

Pregunta 20. Resuelve: $\frac{2x−3}{3x−7}$ > 0.

Pregunta 21. Resuelve: $\frac{3}{x−2}$ < 1.

Pregunta 22. Resuelve: $\frac{1}{x−1}$ ≤ 2.

Pregunta 23. Resuelve: $\frac{4x+3}{2x−5}$ < 6

Pregunta 24. Resuelve: $\frac{5x−6}{x+6}$ < 1.

Pregunta 25. Resuelve: $\frac{5x+8}{4−x}$ < 2.

Pregunta 26. Resuelve: $\frac{x−1}{x+3}$ > 2.

Pregunta 27. Resuelve: $\frac{7x−5}{8x+3}$ > 4.

Pregunta 28. Resuelve: $\frac{x}{x−5}$ > 1/2.

Deja una respuesta Cancelar la respuesta

Pregunta 15. Resuelve: < − 5 en R.

Pregunta 16. Resuelve: ≥ − 3.

Pregunta 17. Resuelve: − 2 < .

Pregunta 18. Resuelve: x−2 ≤

Pregunta 19. Resuelve: < 0.

Pregunta 20. Resuelve: > 0.

Pregunta 21. Resuelve: < 1.

Pregunta 22. Resuelve: ≤ 2.

Pregunta 23. Resuelve: < 6

Pregunta 24. Resuelve: < 1.

Pregunta 25. Resuelve: < 2.

Pregunta 26. Resuelve: > 2.

Pregunta 27. Resuelve: > 4.

Pregunta 28. Resuelve: > 1/2.

Deja una respuesta Cancelar la respuesta

Pregunta 15. Resuelve: $\frac{5−2x}{3}$ < $\frac{x}{6}$ − 5 en R.

Pregunta 16. Resuelve: $\frac{4+2x}{3}$ ≥ $\frac{x}{2}$ − 3.

Pregunta 17. Resuelve: $\frac{2x+3}{5}$ − 2 < $\frac{3(x−2)}{5}$ .

Pregunta 18. Resuelve: x−2 ≤ $\frac{5x+8}{3}$

Pregunta 19. Resuelve: $\frac{6x−5}{4x+1}$ < 0.

Pregunta 20. Resuelve: $\frac{2x−3}{3x−7}$ > 0.

Pregunta 21. Resuelve: $\frac{3}{x−2}$ < 1.

Pregunta 22. Resuelve: $\frac{1}{x−1}$ ≤ 2.

Pregunta 23. Resuelve: $\frac{4x+3}{2x−5}$ < 6

Pregunta 24. Resuelve: $\frac{5x−6}{x+6}$ < 1.

Pregunta 25. Resuelve: $\frac{5x+8}{4−x}$ < 2.

Pregunta 26. Resuelve: $\frac{x−1}{x+3}$ > 2.

Pregunta 27. Resuelve: $\frac{7x−5}{8x+3}$ > 4.

Pregunta 28. Resuelve: $\frac{x}{x−5}$ > 1/2.