Clase 11 Soluciones RD Sharma – Capítulo 15 Inecuaciones lineales – Ejercicio 15.1

Pregunta 1. Resuelve: 12x < 50, cuando

(i) x ∈ R

Solución:

Dado: 12x < 50

Dividiendo ambos lados por 12, obtenemos

12x/ 12 < 50/12

⇒ x < 25/6

Cuando x es un número real, la solución de la inecuación dada es (-∞, 25/6).

(ii) x ∈ Z

Solución:

Dado que, 4 < 25/6 < 5

Entonces, cuando x es un número entero, el valor máximo posible de x es 4.

La solución de la inecuación dada es {…, –2, –1, 0, 1, 2, 3, 4}.

(iii) x ∈ N

Solución:

Dado que 4 < 25/6 < 5

Entonces, cuando x es un número natural, el máximo valor posible de x es 4.

Sabemos que los números naturales parten del 1.

Por lo tanto, la solución de la inecuación dada es {1, 2, 3, 4}.

Pregunta 2. Resuelve: − 4x > 30, cuando

(i) x ∈ R

Solución:

Dado: − 4x > 30

Entonces, cuando dividimos por 4, obtenemos

⇒ − 4x/4 > 30/4

⇒ − x > 15/2

⇒ x < – 15/2

Cuando x es un número real, la solución de la inecuación dada es (-∞, −15/2).

(ii) x ∈ Z

Solución:

Como, − 8 < − 15/2 < − 7

Entonces, cuando x es un número entero, el valor máximo posible de x es − 8.

La solución de la inecuación dada es {…, –11, –10, − 9, −8}.

(iii) x ∈ N

Solución:

Como los números naturales parten del 1 y nunca pueden ser negativos.

Por tanto, cuando x es un número natural, la solución de la inecuación dada es ∅.

Pregunta 3. Resuelve: 4x-2 < 8, cuando

(i) x ∈ R

Solución:

Dado: 4x – 2 < 8

4x – 2 + 2 < 8 + 2

⇒ 4x < 10

Entonces, dividiendo por 4 en ambos lados obtenemos,

4x/4 < 10/4

⇒ x < 5/2

Cuando x es un número real, la solución de la inecuación dada es (-∞, 5/2).

(ii) x ∈ Z

Solución:

Dado que, 2 < 5/2 < 3

Entonces, cuando x es un número entero, el valor máximo posible de x es 2.

La solución de la inecuación dada es {…, –2, –1, 0, 1, 2}.

(iii) x ∈ N

Solución:

Dado que, 2 < 5/2 < 3

Entonces, cuando x es un número natural, el máximo valor posible de x es 2.

Sabemos que los números naturales parten del 1.

La solución de la inecuación dada es {1, 2}.

Pregunta 4. Resuelve: 3x – 7 > x + 1

Solución:

Dado:

3x – 7 > x + 1

⇒ 3x – 7 + 7 > x + 1 + 7

⇒ 3x > x + 8

⇒ 3x – x > x + 8 – x

⇒ 2x > 8

Dividiendo ambos lados por 2, obtenemos

2x/2 > 8/2

⇒ x > 4

∴ La solución de la inecuación dada es (4, ∞).

Pregunta 5. Resuelve: x + 5 > 4x – 10

Solución:

Dado: x + 5 > 4x – 10

⇒ x + 5 – 5 > 4x – 10 – 5

⇒ x > 4x – 15

⇒ 4x – 15 <x

⇒ 4x – 15 – x < x – x

⇒ 3x – 15 < 0

⇒ 3x – 15 + 15 < 0 + 15

⇒ 3x < 15

Dividiendo ambos lados por 3, obtenemos

3x/3 < 15/3

⇒ x < 5

∴ La solución de la inecuación dada es (-∞, 5).

Pregunta 6. Resuelve: 3x + 9 ≥ –x + 19

Solución:

Dado: 3x + 9 ≥ –x + 19

⇒ 3x + 9 – 9 ≥ –x + 19 – 9

⇒ 3x ≥ –x + 10

⇒ 3x + x ≥ –x + 10 + x

⇒ 4x ≥ 10

Dividiendo ambos lados por 4, obtenemos

4x/4 ≥ 10/4

⇒ x ≥ 5/2

∴ La solución de la inecuación dada es [5/2, ∞).

Pregunta 7. Resuelve: 2 (3 – x) ≥ x/5 + 4

Solución:

Dado: 2 (3 – x) ≥ x/5 + 4

⇒ 6 – 2x ≥ x/5 + 4

⇒ 6 – 2x ≥ (x+20)/5

⇒ 5(6 – 2x) ≥ (x + 20)

⇒ 30 – 10x ≥ x + 20

⇒ 30 – 20 ≥x + 10x

⇒ 10 ≥11x

⇒ 11x ≤ 10

Dividiendo ambos lados por 11, obtenemos

11x/11 ≤ 10/11

⇒ x ≤ 10/11

∴ La solución de la inecuación dada es (-∞, 10/11).

Pregunta 8. Resuelve: 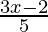$\frac{3x - 2}{5}$ ≤ $\frac{4x - 3}{2}$

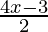
Solución:

Dado: $\frac{3x - 2}{5}$ ≤ $\frac{4x - 3}{2}$

Multiplicando ambos lados por 5 obtenemos,

$\frac{3x - 2}{5}$ × 5 ≤ $\frac{4x - 3}{2}$ × 5

⇒ (3x – 2) ≤ 5(4x – 3)/2

⇒ 3x – 2 ≤ (20x – 15)/2

Multiplicando ambos lados por 2 obtenemos,

(3x – 2) × 2 ≤ (20x – 15)/2 × 2

⇒ 6x – 4 ≤ 20x – 15

⇒ 20x – 15 ≥ 6x – 4

⇒ 20x – 15 + 15 ≥ 6x – 4 + 15

⇒ 20x ≥ 6x + 11

⇒ 20x – 6x ≥ 6x + 11 – 6x

⇒ 14x ≥ 11

Dividiendo ambos lados por 14, obtenemos

14x/14 ≥ 11/14

⇒ x ≥ 11/14

∴ La solución de la inecuación dada es [11/14, ∞).

Pregunta 9. Resuelve: –(x – 3) + 4 < 5 – 2x

Solución:

Dado: –(x – 3) + 4 < 5 – 2x

⇒ –x + 3 + 4 < 5 – 2x

⇒ –x + 7 < 5 – 2x

⇒ –x + 7 – 7 < 5 – 2x – 7

⇒ –x < –2x – 2

⇒ –x + 2x < –2x – 2 + 2x

⇒ x < –2

∴ La solución de la inecuación dada es (–∞, –2).

Pregunta 10. Resuelve: 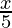$\frac{x}{5}$ < $\frac{3x-2}{4}$ – $\frac{5x-3}{5}$

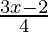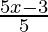
Solución:

Dado: $\frac{x}{5}$ < $\frac{3x-2}{4}$ – $\frac{5x-3}{5}$

⇒ $\frac{x}{5}$ < $\frac{[5(3x-2) - 4(5x-3)]}{4(5)}$

⇒ $\frac{x}{5}$ < $\frac{[15x - 10 - 20x + 12]}{20}$

⇒ $\frac{x}{5}$ < $\frac{[2 - 5x]}{20}$

Multiplicando ambos lados por 20 obtenemos,

$\frac{x}{5}$ × 20 < $\frac{[2 - 5x]}{20}$ × 20

⇒ 4x < 2 – 5x

⇒ 4x + 5x < 2 – 5x + 5x

⇒ 9x < 2

Dividiendo ambos lados por 9, obtenemos

9x/9 < 2/9

⇒ x < 2/9

∴ La solución de la inecuación dada es (-∞, 2/9).

Pregunta 11. Resuelve: $\frac{[2(x-1)]}{5}$ ≤ $\frac{[3(2+x)]}{7}$

Solución:

Dado: $\frac{[2(x-1)]}{5}$ ≤ $\frac{[3(2+x)]}{7}$

⇒ $\frac{(2x - 2)}{5}$ ≤ $\frac{(6 + 3x)}{7}$

Multiplicando ambos lados por 5 obtenemos,

$\frac{(2x - 2)}{5}$ × 5 ≤ $\frac{(6 + 3x)}{7}$ × 5

⇒ 2x – 2 ≤ $\frac{5(6 + 3x)}{7}$

⇒ 7 (2x – 2) ≤ 5 (6 + 3x)

⇒ 14x – 14 ≤ 30 + 15x

⇒ 14x – 14 + 14 ≤ 30 + 15x + 14

⇒ 14x ≤ 44 + 15x

⇒ 14x – 44 ≤ 44 + 15x – 44

⇒ 14x – 44 ≤ 15x

⇒ 15x ≥ 14x – 44

⇒ 15x – 14x ≥ 14x – 44 – 14x

⇒ x ≥ –44

∴ La solución de la inecuación dada es [–44, ∞).

Pregunta 12. Resuelve: 5x/2 + 3x/4 ≥ 39/4

Solución:

Dado: 5x/2 + 3x/4 ≥ 39/4

Al tomar MCM, obtenemos:

$\frac{[2(5x)+3x]}{4}$ ≥ 39/4

⇒ 13x/4 ≥ 39/4

Multiplicando ambos lados por 4 obtenemos,

13x/4 × 4 ≥ 39/4 × 4

⇒ 13x ≥ 39

Dividiendo ambos lados por 13, obtenemos

13x/13 ≥ 39/13

⇒ x ≥ 39/13

⇒ x ≥ 3

∴ La solución de la inecuación dada es [3, ∞).

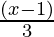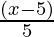Pregunta 13. Resuelve: $\frac{(x - 1)}{3}$ + 4 < $\frac{(x - 5)}{5}$ – 2

Solución:

Dado: $\frac{(x - 1)}{3}$ + 4 < $\frac{(x - 5)}{5}$ – 2

Restando ambos lados por 4 obtenemos,

⇒ $\frac{(x - 1)}{3}$ + 4 – 4 < $\frac{(x - 5)}{5}$ – 2 – 4

⇒ $\frac{(x - 1)}{3}$ < $\frac{(x - 5)}{5}$ – 6

⇒ $\frac{(x - 1)}{3}$ < $\frac{(x - 5 - 30)}{5}$

⇒ $\frac{(x - 1)}{3}$ < $\frac{(x - 35)}{5}$

Después de la multiplicación cruzada, obtenemos,

5 (x-1) < 3 (x-35)

⇒ 5x – 5 < 3x – 105

⇒ 5x – 5 + 5 < 3x – 105 + 5

⇒ 5x < 3x – 100

⇒ 5x – 3x < 3x – 100 – 3x

⇒ 2x < –100

Dividiendo ambos lados por 2, obtenemos

2x/2 < -100/2

⇒ x < -50

∴ La solución de la inecuación dada es (-∞, -50).

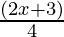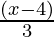Pregunta 14. Resuelve: $\frac{(2x + 3)}{4}$ – 3 < $\frac{(x - 4)}{3}$ – 2

Solución:

Dado: $\frac{(2x + 3)}{4}$ – 3 < $\frac{(x - 4)}{3}$ – 2

Sumando 3 en ambos lados obtenemos,

$\frac{(2x + 3)}{4}$ – 3 + 3 < $\frac{(x - 4)}{3}$ – 2 + 3

⇒ $\frac{(2x + 3)}{4}$ < $\frac{(x - 4)}{3}$ + 1

⇒ $\frac{(2x + 3)}{4}$ < $\frac{(x - 4 + 3)}{3}$

⇒ $\frac{(2x + 3)}{4}$ < $\frac{(x - 1)}{3}$

Después de la multiplicación cruzada, obtenemos,

3(2x + 3) < 4(x – 1)

⇒ 6x + 9 < 4x – 4

⇒ 6x + 9 – 9 < 4x – 4 – 9

⇒ 6x < 4x – 13

⇒ 6x – 4x < 4x – 13 – 4x

⇒ 2x < –13

Dividiendo ambos lados por 2, obtenemos

2x/2 < -13/2

⇒ x < -13/2

∴ La solución de la inecuación dada es (-∞, -13/2).

Publicación traducida automáticamente

Artículo escrito por prabhjotkushparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 11 Soluciones RD Sharma – Capítulo 15 Inecuaciones lineales – Ejercicio 15.1 | Serie 1

Pregunta 1. Resuelve: 12x < 50, cuando

(i) x ∈ R

(ii) x ∈ Z

(iii) x ∈ N

Pregunta 2. Resuelve: − 4x > 30, cuando

(i) x ∈ R

(ii) x ∈ Z

(iii) x ∈ N

Pregunta 3. Resuelve: 4x-2 < 8, cuando

(i) x ∈ R

(ii) x ∈ Z

(iii) x ∈ N

Pregunta 4. Resuelve: 3x – 7 > x + 1

Pregunta 5. Resuelve: x + 5 > 4x – 10

Pregunta 6. Resuelve: 3x + 9 ≥ –x + 19

Pregunta 7. Resuelve: 2 (3 – x) ≥ x/5 + 4

Pregunta 8. Resuelve: $\frac{3x - 2}{5}$ ≤ $\frac{4x - 3}{2}$

Pregunta 9. Resuelve: –(x – 3) + 4 < 5 – 2x

Pregunta 10. Resuelve: $\frac{x}{5}$ < $\frac{3x-2}{4}$ – $\frac{5x-3}{5}$

Pregunta 11. Resuelve: $\frac{[2(x-1)]}{5}$ ≤ $\frac{[3(2+x)]}{7}$

Pregunta 12. Resuelve: 5x/2 + 3x/4 ≥ 39/4

Pregunta 13. Resuelve: $\frac{(x - 1)}{3}$ + 4 < $\frac{(x - 5)}{5}$ – 2

Pregunta 14. Resuelve: $\frac{(2x + 3)}{4}$ – 3 < $\frac{(x - 4)}{3}$ – 2

Deja una respuesta Cancelar la respuesta

Pregunta 1. Resuelve: 12x < 50, cuando

(i) x ∈ R

(ii) x ∈ Z

(iii) x ∈ N

Pregunta 2. Resuelve: − 4x > 30, cuando

(i) x ∈ R

(ii) x ∈ Z

(iii) x ∈ N

Pregunta 3. Resuelve: 4x-2 < 8, cuando

(i) x ∈ R

(ii) x ∈ Z

(iii) x ∈ N

Pregunta 4. Resuelve: 3x – 7 > x + 1

Pregunta 5. Resuelve: x + 5 > 4x – 10

Pregunta 6. Resuelve: 3x + 9 ≥ –x + 19

Pregunta 7. Resuelve: 2 (3 – x) ≥ x/5 + 4

Pregunta 8. Resuelve: ≤

Pregunta 9. Resuelve: –(x – 3) + 4 < 5 – 2x

Pregunta 10. Resuelve: < –

Pregunta 11. Resuelve: ≤

Pregunta 12. Resuelve: 5x/2 + 3x/4 ≥ 39/4

Pregunta 13. Resuelve: + 4 < – 2

Pregunta 14. Resuelve: – 3 < – 2

Deja una respuesta Cancelar la respuesta

Pregunta 8. Resuelve: $\frac{3x - 2}{5}$ ≤ $\frac{4x - 3}{2}$

Pregunta 10. Resuelve: $\frac{x}{5}$ < $\frac{3x-2}{4}$ – $\frac{5x-3}{5}$

Pregunta 11. Resuelve: $\frac{[2(x-1)]}{5}$ ≤ $\frac{[3(2+x)]}{7}$

Pregunta 13. Resuelve: $\frac{(x - 1)}{3}$ + 4 < $\frac{(x - 5)}{5}$ – 2

Pregunta 14. Resuelve: $\frac{(2x + 3)}{4}$ – 3 < $\frac{(x - 4)}{3}$ – 2