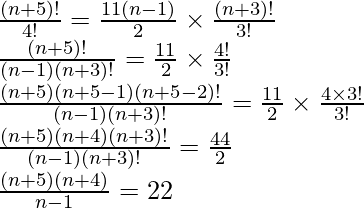Pregunta 11. Si P(n, 5) : P(n, 3) = 2 : 1, encuentra n.
Solución:
Dado:
P(n, 5) : P(n, 3) = 2 : 1
Después de aplicar la fórmula,
P (n, r) =
P (n, 5) =
P (n, 3) =
Entonces, de la pregunta,
Después de sustituir los valores en la expresión anterior obtendremos,
(n-3)(n-4) = 2
n 2 – 3n – 4n + 12 = 2
n 2 – 7n + 12 – 2 = 0
norte 2 – 7n + 10 = 0
n 2 – 5n – 2n + 10 = 0
n (n – 5) – 2 (n – 5) = 0
(n-5) (n-2) = 0
n = 5 o 2
Para, P (n, r): n ≥ r
∴ n = 5 [para, P (n, 5)]
Pregunta 12. Demostrar que:
1. PAG (1, 1) + 2. PAG (2, 2) + 3 . PAG (3, 3) + … + norte . P(n, n) = P(n + 1, n + 1) – 1.
Solución:
Usando la fórmula,
P (n, r) =
P (n, n) =
=
= n! [Ya que, 0! = 1]
Considere LHS:
= 1. P(1, 1) + 2. P(2, 2) + 3. P(3, 3) + … + norte . P(n, n)
= 1,1! + 2.2! + 3.3! +………+ nn! [Ya que, P(n, n) = n!]
= (2! – 1!) + (3! – 2!) + (4! – 3!) + ……… + (n! – (n – 1)!) + ((n+1)! – n !)
= 2! – 1! + 3! – 2! + 4! – 3! + ……… + n! – (n – 1)! + (n+1)! – n!
= (n + 1)! – 1!
= (n + 1)! – 1 [Ya que, P (n, n) = n!]
= P(n+1, n+1) – 1
= lado derecho
Por lo tanto Probado.
Pregunta 13. Si P(15, r – 1) : P(16, r – 2) = 3 : 4, encuentre r.
Solución:
Dado:
P(15, r – 1) : P(16, r – 2) = 3 : 4
Después de aplicar la fórmula,
P (n, r) =
P (15, r – 1) =
=
P (16, r – 2) =
=
Entonces, de la pregunta,
Después de sustituir los valores en la expresión anterior obtendremos,
(18 – r) (17 – r) = 12
306 – 18r – 17r + r2 = 12
306 – 12 – 35r + r2 = 0
r 2 – 35r + 294 = 0
r 2 – 21r – 14r + 294 = 0
r(r-21)-14(r-21) = 0
(r-14) (r-21) = 0
r = 14 o 21
Para, P(n, r): r ≤ n
∴ r = 14 [para, P(15, r – 1)]
Pregunta 14. n+5 P n +1 = 11(n – 1)/2 n+3 P n , encuentra n.
Solución:
Dado:
n+5 PAG n+1 = 11(n – 1)/2 n +3 PAG norte
P (n + 5, n + 1) = 11 (n – 1)/2 P (n + 3, n)
Usando la fórmula,
P (n, r) =
P(n + 5, n=1) =
P(n + 3, n) =
Entonces, de la pregunta
P(n + 5, n + 1) = 11(n -1)/2P(n + 3, n)
Después de sustituir los valores en la expresión anterior obtenemos,
(n + 5) (n + 4) = 22 (n – 1)
n2 + 4n + 5n + 20 = 22n – 22
n2 + 9n + 20 – 22n + 22 = 0
n 2 – 13 n + 42 = 0
n 2 – 6n – 7n + 42 = 0
n(n-6)-7(n-6) = 0
(n-7) (n-6) = 0
n = 7 o 6
∴ El valor de n puede ser 6 o 7.
Pregunta 15. ¿De cuántas maneras pueden hacer cola cinco niños?
Solución:
Número de arreglos de ‘n’ cosas tomadas todas a la vez = P (n, n)
Por eso,
Después de aplicar la fórmula,
P (n, r) =
El número total de formas en que cinco niños pueden hacer cola = el número de arreglos de 5 cosas tomadas todas a la vez = P (5, 5)
De este modo,
PAG (5, 5) =
=
= 5! [Ya que, 0! = 1]
= 5 × 4 × 3 × 2 × 1
= 120
Por lo tanto, el número de formas en que cinco niños pueden hacer cola son 120.
Pregunta 16. De entre los 36 maestros de una escuela, se nombrará un director y un subdirector. ¿De cuántas maneras se puede hacer esto?
Solución:
Dado:
El número total de maestros en una escuela = 36
Como sabemos que, número de arreglos de n cosas tomadas r a la vez = P(n, r)
Después de aplicar la fórmula,
P (n, r) =
∴ El número total de formas en que se puede hacer esto = el número de arreglos de 36 cosas tomadas 2 a la vez = P(36, 2)
PAG (36, 2) =
=
=
= 36 × 35
= 1260
Por lo tanto, el número de formas en que se nombrarán un director y un subdirector de un total de 36 maestros en la escuela es 1260.
Publicación traducida automáticamente
Artículo escrito por yashchuahan y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
![Procesado por QuickLaTeX.com \frac{\frac{n!}{(n-5)!}}{\frac{n!}{(n-3)!}}=\frac{2}{1}\\ \frac{n!}{(n-5)!}\times\frac{(n-3)!}{n!}=\frac{2}{1} \\\frac{(n - 3)! }{ (n - 5)!} = \frac{2}{1}\\ \frac{[(n - 3) (n - 3 - 1) (n - 3 - 2)!] }{ (n - 5)!} = \frac{2}{1}\\ \frac{[(n - 3) (n - 4) (n - 5)!]} { (n - 5)!} = \frac{2}{1}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4100bc5754b9cf07fe343e5a48c34ddb_l3.png)

![Rendered by QuickLaTeX.com \frac{\frac{15!}{(16-r)!}}{\frac{16!}{(18-r)!}}=\frac{3}{4}\\ \frac{15! }{ (16 - r)!} × \frac{(18 - r)! }{ 16!} = \frac{3}{4}\\ \frac{15! }{ (16 - r)!} × \frac{[(18 - r) (18 - r - 1) (18 - r - 2)!]}{(16×15!)} = \frac{3}{4}\\ \frac{1}{(16 - r)!} × \frac{[(18 - r) (17 - r) (16 - r)!]}{16} = \frac{3}{4}\\ (18 - r) (17 - r) = \frac{3}{4} × 16\\](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-39fac7143003a909f3a1af4ef91aaca6_l3.png)