Pregunta 1. Evalúe cada uno de los siguientes:
(i) 8 P 3
(ii) 10 P 4
(iii) 6 P 6
(iv) P (6, 4)
Solución:
(i) 8 P 3
Como sabemos que, 8 P 3 se puede escribir como P (8, 3)
Después de aplicar la fórmula,
P (n, r) =
PAG (8, 3)
= 8 × 7 × 6
= 336
∴ 8 P 3 = 336
(ii) 10 P 4
Como sabemos que, 10 P 4 se puede escribir como P (10, 4)
Después de aplicar la fórmula,
P (n, r) =
PAG (10, 4) =
= 10 × 9 × 8 × 7
= 5040
∴ 10 P 4 = 5040
(iii) 6 P 6
Como sabemos que, 6 P 6 se puede escribir como P (6, 6)
Después de aplicar la fórmula,
P (n, r) =
P (6, 6) =
{Ya que, 0! = 1}
= 6 × 5 × 4 × 3 × 2 × 1
= 720
∴ 6 P 6 = 720
(iv) P (6, 4)
Después de aplicar la fórmula,
P (n, r) =
PAG (6, 4) =
= 6 × 5 × 4 × 3
= 360
∴ PAG (6, 4) = 360
Pregunta 2. Si P (5, r) = P (6, r – 1), encuentra r.
Solución:
Dado:
PAG (5, r) = PAG (6, r – 1)
Después de aplicar la fórmula,
P (n, r) =
P (5, r) =
P (6, r-1) =
Entonces, de la pregunta,
PAG (5, r) = PAG (6, r – 1)
Entonces, después de sustituir los valores en la expresión anterior, obtendremos,
Al evaluar,
(7 – r) (6 – r) = 6
42 – 6r – 7r + r2 = 6
42 – 6 – 13r + r2 = 0
r 2 – 13r + 36 = 0
r 2 – 9r – 4r + 36 = 0
r(r-9)-4(r-9) = 0
(r-9) (r-4) = 0
r = 9 o 4
Para, P (n, r): r ≤ n
∴ r = 4 [para, P (5, r)]
Pregunta 3. Si 5 P(4, n) = 6 P(5, n – 1), encuentra n.
Solución:
Dado:
5 P(4, n) = 6 P(5, n – 1)
Después de aplicar la fórmula,
P (n, r) =
P (4, n) =
P (5, n-1) =
Entonces, de la pregunta,
5 P(4, n) = 6 P(5, n – 1)
Entonces, después de sustituir los valores en la expresión anterior, obtendremos,
Al evaluar,
(6 – n) (5 – n) = 6
30 – 6n – 5n + n2 = 6
30 – 6 – 11n + n 2 = 0
norte 2 – 11n + 24 = 0
n 2 – 8n – 3n + 24 = 0
n(n-8)-3(n-8) = 0
(n-8) (n-3) = 0
n = 8 o 3
Para, P (n, r): r ≤ n
∴ n = 3 [para, P (4, n)]
Pregunta 4. Si P(n, 5) = 20 P(n, 3), encuentra n.
Solución:
Dado:
P(n, 5) = 20 P(n, 3)
Después de aplicar la fórmula,
P (n, r) =
P (n, 5) =
P (n, 3) =
Entonces, de la pregunta,
P(n, 5) = 20 P(n, 3)
Después de sustituir los valores en la expresión anterior obtendremos,
Al evaluar,
(n-3) (n-4) = 20
n 2 – 3n – 4n + 12 = 20
n 2 – 7n + 12 – 20 = 0
n 2 – 7 n – 8 = 0
norte 2 – 8n + norte – 8 = 0
n(n-8)-1(n-8) = 0
(n-8) (n-1) = 0
n = 8 o 1
Para, P(n, r): n ≥ r
∴ n = 8 [para, P(n, 5)]
Pregunta 5. Si n P 4 = 360, encuentra el valor de n.
Solución:
Dado:
n P 4 = 360
n P 4 se puede escribir como P (n , 4)
Después de aplicar la fórmula,
P (n, r) =
P (n, 4) =
Entonces, de la pregunta,
norte PAG 4 = PAG ( n , 4) = 360
Después de sustituir los valores en la expresión anterior obtendremos,
= 360
= 360
n (n – 1) (n – 2) (n – 3) = 360
norte (n – 1) (n – 2) (n – 3) = 6×5×4×3
Al comparar,
El valor de n es 6.
Pregunta 6. Si P(9, r) = 3024, encuentre r.
Solución:
Dado:
P (9, r) = 3024
Después de aplicar la fórmula,
P (n, r) =
P (9, r) =
Entonces, de la pregunta,
P (9, r) = 3024
Sustituyendo los valores obtenidos en la expresión anterior obtenemos,
= 3024
=
=
=
(9 – r)! = 5!
9 – r = 5
-r = 5 – 9
-r = -4
∴ El valor de r es 4.
Pregunta 7. Si P (11, r) = P (12, r – 1), encuentre r.
Solución:
Dado:
PAG (11, r) = PAG (12, r – 1)
Después de aplicar la fórmula,
P (n, r) =
P (11, r) =
P (12, r-1) =
=
=
Entonces, de la pregunta,
PAG (11, r) = PAG (12, r – 1)
Después de sustituir los valores en la expresión anterior obtendremos,
Al evaluar,
= 12
(13 – r) (12 – r) = 12
156 – 12r – 13r + r2 = 12
156 – 12 – 25r + r2 = 0
r 2 – 25r + 144 = 0
r 2 – 16r – 9r + 144 = 0
r(r-16)-9(r-16) = 0
(r-9) (r-16) = 0
r = 9 o 16
Para, P (n, r): r ≤ n
∴ r = 9 [para, P (11, r)]
Pregunta 8. Si P(n, 4) = 12. P(n, 2), halla n.
Solución:
Dado:
PAG (n, 4) = 12. PAG (n, 2)
Después de aplicar la fórmula,
P (n, r) =
P (n, 4) =
P (n, 2) =
Entonces, de la pregunta,
PAG (n, 4) = 12. PAG (n, 2)
Después de sustituir los valores en la expresión anterior obtendremos,
Al evaluar,
= 12
= 12
= 12
(n-2) (n-3) = 12
n 2 – 3n – 2n + 6 = 12
n 2 – 5n + 6 – 12 = 0
n 2 – 5 n – 6 = 0
norte 2 – 6n + norte – 6 = 0
n (n – 6) – 1 (n – 6) = 0
(n-6) (n-1) = 0
n = 6 o 1
Para, P (n, r): n ≥ r
∴ n = 6 [para, P (n, 4)]
Pregunta 9. Si P(n – 1, 3) : P(n, 4) = 1 : 9, encuentre n.
Solución:
Dado:
PAG (n – 1, 3): PAG (n, 4) = 1 : 9
Después de aplicar la fórmula,
P (n, r) =
P (n – 1, 3) =
=
P (n, 4) =
Entonces, de la pregunta,
Después de sustituir los valores en la expresión anterior obtendremos,
norte = 9
∴ El valor de n es 9.
Pregunta 10. Si P(2n – 1, n) : P(2n + 1, n – 1) = 22 : 7 encuentra n.
Solución:
Dado:
P(2n – 1, n) : P(2n + 1, n – 1) = 22 : 7
Después de aplicar la fórmula,
P (n, r) =
P (2n – 1, n) =
=
P (2n + 1, n – 1) =
=
Entonces, de la pregunta,
Después de sustituir los valores en la expresión anterior obtendremos,
7(n+2) (n+1) = 22×2 (2n+1)
7(n 2 + n + 2n + 2) = 88n + 44
7(n 2 + 3n + 2) = 88n + 44
7n 2 + 21n + 14 = 88n + 44
7n 2 + 21n – 88n + 14 – 44 = 0
7n 2 – 67n – 30 = 0
7n 2 – 70n + 3n – 30 = 0
7n(n-10) + 3(n-10) = 0
(n – 10) (7n + 3) = 0
n = 10,
Como sabemos que, n ≠
∴ El valor de n es 10.
Publicación traducida automáticamente
Artículo escrito por yashchuahan y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
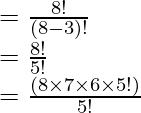
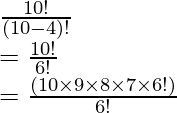
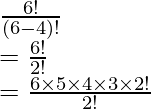
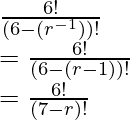
![Rendered by QuickLaTeX.com \frac{(7-r)!}{(5-r)!}=\frac{6!}{5!}\\ \frac{[(7-r)(7-r-1)(7-r-2)!]}{(5-r)!}=\frac{(6\times5!)}{5!}\\ \frac{[(7-r)(6-r)(5-r)!]}{(5-r)!}=6](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b57eab3c306a4ced71cfca075aa0b2be_l3.png)
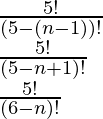
![Rendered by QuickLaTeX.com \frac{(6 - n)!}{(4 - n)!}= \frac{6}{5} × \frac{5!}{4!}\\ \frac{[(6 - n) (6 - n - 1) (6 - n - 2)!]}{(4 - n)!} = \frac{(6 × 5 × 4!)}{ (5 × 4!)}\\ \frac{[(6 - n) (5 - n) (4 - n)!]}{(4 - n)!} = 6](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-fa65f166dbe84a75808daf2b328d9db8_l3.png)
![Rendered by QuickLaTeX.com \frac{n! (n - 3)!}{n! (n - 5)!} = 20\\ \frac{[(n - 3) (n - 3 - 1) (n - 3 - 2)!]} {(n - 5)!} = 20\\ \frac{[(n - 3) (n - 4) (n - 5)!]}{(n - 5)!} = 20](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-dd32a59c1a73b7535f49452220651b48_l3.png)
![Rendered by QuickLaTeX.com \frac{\frac{[(n - 1)!}{ (n - 4)!]}} { \frac{[n!}{(n - 4)!]}} = \frac{1}{9}\\ \frac{[(n - 1)! }{ (n - 4)!]} × \frac{[(n - 4)! }{ n!]} = \frac{1}{9}\\ \frac{(n - 1)!}{n!} = \frac{1}{9}\\ \frac{(n - 1)!}{n (n - 1)!} = \frac{1}{9}\\ \frac{1}{n} = \frac{1}{9}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-39129ec1339d8399d601869706f1fb05_l3.png)
![Rendered by QuickLaTeX.com \frac{\frac{(2n - 1)! }{ (n - 1)!} }{\frac{ (2n + 1)! }{ (n + 2)!}} = \frac{22}{7}\\ \frac{(2n - 1)! }{ (n - 1)!} × \frac{(n + 2)! }{ (2n + 1)!} = \frac{22}{7}\\ \frac{(2n - 1)! }{ (n - 1)!} × \frac{[(n + 2) (n + 2 - 1) (n + 2 - 2) (n + 2 - 3)!] }{ [(2n + 1) (2n + 1 - 1) (2n + 1 - 2)]} = \frac{22}{7}\\ \frac{[(2n - 1)! }{ (n - 1)!]} × \frac{[(n + 2) (n + 1) n(n - 1)!] }{ [(2n + 1) 2n (2n - 1)!]} = \frac{22}{7}\\ \frac{[(n + 2) (n + 1)] }{ (2n + 1)2} = \frac{22}{7}\\](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-97faef314bd6636b7a028ac4bb471bdd_l3.png)