Clase 11 Soluciones RD Sharma – Capítulo 16 Permutaciones – Ejercicio 16.4

Pregunta 1. ¿De cuántas maneras se pueden ordenar las letras de la palabra ‘FRACASO’ de modo que las consonantes ocupen solo posiciones impares?

Solución:

De la palabra dada, obtenemos

F, L, R = 3 consonantes

A, I, U, E = 4 vocales

1, 3, 5, 7 = 4 posiciones impares posibles

De estas 4 posiciones, seleccione 3 posiciones para las 3 consonantes dadas = ⁴ P ₃ = 4 formas 

Ahora, para estas posiciones, ¡formas de organizar las consonantes = 3! = 6

¡Y las formas de organizar las vocales en las posiciones restantes son = 4! = 24 

Formas totales = 4 x 6 x 24 = 576 

Pregunta 2. ¿De cuántas maneras se pueden ordenar las letras de la palabra ‘EXTRAÑO’ para que

(i) ¿Las vocales se juntan?

(ii) ¿Las vocales nunca se juntan? Y

(iii) ¿Las vocales ocupan sólo los lugares impares?

Solución:

(i) Se dan 2 vocales, para que estén juntas deje que la primera de dos vocales ocupe una posición p 

Ahora, hay 6 formas en las que se puede elegir p.

(Todas las 7 posiciones excepto la última posición, porque si la primera vocal 

viene en la última posición, no quedará ninguna posición allí para la segunda vocal)

Para cada p elegida, las vocales se pueden poner en dos órdenes (AE, EA) = 2 formas

¡Las letras restantes se pueden organizar en = 5! = 120 maneras

Formas totales = Formas de elegir posiciones para las vocales x 

                      Maneras de ordenar las vocales x 

                     Formas de organizar las letras restantes.

= 6x2x120 = 1440 

(ii) Sea la primera vocal en la posición p. 

p se puede elegir de 6 maneras diferentes (1 a 6). 

Cuando la primera vocal está en p, la segunda puede estar entre p+2 y 7, de modo que no sea consecutiva.

 = 7 – (p + 2) + 1 = (6 – p) vías 

Caso 1: p = 1 ⇒ 6 – p = 5 

Caso 2: p=2 ⇒ 6 – p = 4   

y así sucesivamente hasta 6 – p = 0 para el Caso 6. 

No. de formas de seleccionar las posiciones de las vocales en la palabra = 5 + 4 + 3 + 2 + 1 + 0 = 15 

Para cada selección, formas de poner las vocales = 2 (AE y EA)

Formas de poner las letras restantes = 5! = 120

Formas totales = 15 x 2 x 120 = 3600

(iii) Elegir 2 posiciones impares de 4 = ⁴ P ₂ = 4 x 3 / 2 = 6 

Maneras de colocar dos vocales en posiciones seleccionadas = 2! = 2

¡Las formas de organizar otras letras son = 5! = 120

Formas totales = 6 x 2 x 120 = 1440

Pregunta 3. ¿Cuántas palabras se pueden formar con las letras de la palabra ‘SUNDAY’? ¿Cuántos de estos comienzan con D?

Solución:

Número total de letras presentes en la palabra dada = 6

Entonces, ¡formas de organizar 6 letras para obtener las palabras = 6! = 720

Ahora, cuando D se fija en la posición 1, ¡los 5 restantes se pueden organizar de formas = 5! = 120  

Pregunta 4. ¿Cuántas palabras se pueden formar con las letras de la palabra ‘ORIENTAL’ de modo que las vocales siempre ocupen los lugares impares?

Solución:

De la palabra dada, obtenemos 4 vocales y 4 posiciones impares posibles (1, 3, 5, 7)

Entonces, ¡las formas de ordenar las vocales = 4! = 24

Formas de organizar las letras consonantes = 4! = 24 

Formas totales = 24 x 24 = 576   

Pregunta 5. ¿Cuántas palabras diferentes se pueden formar con las letras de la palabra ‘SUNDAY’? ¿Cuántas de las palabras comienzan con N? ¿Cuántos comienzan con N y terminan con Y?

Solución:

Número total de letras presentes en la palabra dada = 6

Ahora, Formas de ordenar las 6 letras para obtener las palabras = 6! = 720 

Así que ahora encontramos cuántas palabras comienzan con N

Deje que la N fija en la primera posición y la letra restante sea 5

¡Entonces el arreglo de 5 letras puede estar en 5! caminos = 120 caminos

Ahora encuentre cuántos comienzan con N y terminan en Y

Deje que Y en la posición número 6 y N en la posición número 1 y la letra restante sea 4

Entonces, ¡el arreglo de 4 letras puede estar en 4! caminos = 24 caminos

Pregunta 6. ¿Cuántas palabras diferentes se pueden formar a partir de las letras de la palabra ‘GANESHPURI’? En cuantas de estas palabras:

(i) ¿La letra G siempre ocupa el primer lugar?

(ii) ¿La letra P y la I ocupan respectivamente el primer y último lugar?

(iii) ¿Están las vocales siempre juntas?

(iv) ¿Las vocales siempre ocupan lugares pares?

Solución:

Dado: número total de letras presentes en la palabra dada = 10

(i) Fije G en la posición número 1 y las letras restantes son 9

¡Entonces, las letras restantes se pueden organizar 9! = 51840 maneras 

(ii) La letra P y I respectivamente ocupan el primer y último lugar y las letras restantes son 8

¡Entonces, las letras restantes se pueden organizar 8! = 5760 maneras

(iii) Número total de vocales presentes = 4 

La primera vocal puede estar al máximo en la posición 7 (de lo contrario, las vocales restantes

                                                                          no tiene suficientes puestos requeridos)

Entonces, de 1 a 7 posiciones, la primera vocal se puede poner en ⁷ P ₁ = 7 formas 

El resto se colocará en las siguientes posiciones consecutivas en la palabra. (entonces 1 manera)

Formas de seleccionar las posiciones de las vocales = Formas de poner la primera vocal x Formas de poner las vocales restantes 

= 7 x 1 = 7 formas 

Formas de organizar las 4 vocales en estas 4 posiciones seleccionadas = ¡4! = 24 maneras

¡Las formas de organizar las letras consonantes serán = 6! = 720 maneras 

Total de palabras que tienen las vocales siempre juntas = Formas de elegir las posiciones de las vocales x 

                                                                            Maneras de ordenar las vocales x 

                                                                            Maneras de ordenar las consonantes. 

= 7x24x720 

= 120960

(iv) 5 posiciones posibles que son pares (2, 4, 6, 8, 10) 

Tenemos 4 vocales y necesitamos elegir 4 posiciones pares = ⁵ P ₄ = 5 formas 

¡Maneras de organizar estas 4 vocales = 4! = 24

Maneras de ordenar las 6 consonantes = 6! = 720

Palabras totales = 5 x 24 x 720 

= 86400

Pregunta 7. ¿Cuántas permutaciones se pueden formar con las letras de la palabra ‘VOCAL’, cuando 

(i) ¿No hay restricción en las letras?                                                  

(ii) Cada palabra comienza con E?

(iii) ¿Cada palabra comienza con O y termina con L?                                  

(iv) ¿Todas las vocales se juntan?

(v) ¿Todas las consonantes vienen juntas?

Solución:

Dado: Número total de letras = 6

(i) ¡Las formas de ordenar 6 letras son = 6! = 720

(ii) Fijar E en la primera posición y las letras restantes son 5 

Entonces, ¡las letras restantes se pueden ordenar = 5! = 120 maneras

(iii) Fije O en la primera y L en la última posición. Así que las 4 letras restantes

¡Estas 4 letras se pueden arreglar = 4! = 24 maneras

(iv) 2 vocales juntas pueden considerarse 1 símbolo = 2 formas para este nuevo símbolo (EO y OE)   

1 símbolo y 4 letras = 5 cosas se van a arreglar de manera que el número de formas = 5! =120

Formas totales = 120 x 2 = 240

(v) ¡Consonantes juntas = VWLS son 1 grupo = 4! maneras 

Grupo de consonantes y 2 vocales = 3 cosas = 3! maneras de arreglar

Formas totales = 4! x3! = 144

Pregunta 8. ¿Cuántas palabras se pueden formar con las letras de la palabra ‘ARTÍCULO’, de modo que las vocales ocupen lugares pares?

Solución:

En la palabra dada, tenemos 3 vocales y también 3 posiciones pares allí 

¡Así que 3! Formas de ocupar lugares para las vocales.

Para consonantes = 4! = 24 maneras  

Palabras totales = 3! ¡x4! = 144

Pregunta 9. ¿De cuántas maneras se puede formar un doble mixto de tenis sobre hierba con siete parejas casadas si ningún marido y mujer juegan en el mismo set?

Solución:

2 equipos con 1 hombre y 1 mujer

Necesito seleccionar 2 hombres, por lo que el número de formas es = ⁷ P ₂ = 21 

Necesita seleccionar 2 mujeres de 5 (excepto esposas de hombres seleccionados), formas = ⁵ P ₂ = 10 

Ahora, las formas de asignar equipos a hombres son = 2 (1er hombre al equipo A o al equipo B)

Del mismo modo, para las mujeres también = 2 formas

Número de vías requeridas = 21 x 10 x 2 x 2 = 840  

Pregunta 10. M hombres y n mujeres deben sentarse en una fila para que no se sienten dos mujeres juntas. Si m > n, demuestre que el número de maneras en que pueden sentarse como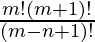    

Solución:

¡Primero sentemos a los hombres = m! maneras 

Ahora, se crean m+1 espacios para que las mujeres se sienten. 

(antes del 1er hombre, entre dos hombres consecutivos, después del último hombre sentado)  

De estos m+1 espacios, necesitamos elegir n espacios para las mujeres = ^m+1 P _n formas posibles

Organizar mujeres en n! maneras después de seleccionar asientos para ellos arriba.

Total de formas de sentarse = m! xn! x(m+1)! / ( (m + 1 – n!) xn! )

= m! (m+1)! / (m+1-n)!

Por lo tanto, se muestra.  

Pregunta 11. ¿Cuántas palabras (con o sin significado de diccionario) se pueden formar con las letras de la palabra LUNES, suponiendo que no se repita ninguna letra, si 

(i) ¿Se usan 4 letras a la vez?                                                    

(ii) ¿Se utilizan todas las letras a la vez?

(iii) ¿Se usan todas las letras, pero la primera es la vocal?

Solución:

(i) Seleccione 4 letras de 6 = ⁶ P ₄ = 6 x 5 / 2 = 15  

Maneras de organizar estos = 4! = 24

Total de tales palabras posibles = 15 x 24 = 360

(ii) ¡Número de tales palabras = 6! = 720

(iii) Posibilidades de primera posición = 2 (O o A)  

¡El número de arreglos para otras posiciones en la palabra es = 5! 

¡Palabras totales = 2 x 5! = 240            

Pregunta 12. ¿Cuántas palabras de tres letras se pueden formar con las letras de la palabra ‘ORIENTAL’?

Solución:

Número total de letras presentes en la palabra dada = 4

Seleccione 3 letras de 8 = ⁸ P ₃  = 56 formas   

¡Tenemos 3! maneras de arreglar 

Por lo tanto, el total de palabras = 56 x 3! = 336