Clase 11 Soluciones RD Sharma – Capítulo 17 Combinaciones – Ejercicio 17.3

Pregunta 1: ¿Cuántas palabras diferentes, cada una con 2 vocales y 3 consonantes, se pueden formar con 5 vocales y 17 consonantes?

Solución:

Dado, la palabra contiene 2 vocales y 3 consonantes.

Entonces, debemos elegir 2 vocales de 5 vocales y 3 consonantes de 17 consonantes.

Esto se puede hacer de $^5C_3.^{17}C_3$ maneras.

Además, necesitamos una cantidad de palabras diferentes, ¡podemos organizar palabras de 5 letras en 5! maneras.

Por lo tanto, Número total de vías = $(^5C_3.^{17}C_3)5!$

⇒ 6800 × 120 = 816000

Pregunta 2: Hay 10 personas nombradas P ₁ ,P ₂ ,P ₃ ….P ₁₀ de 10 personas, 5 personas deben colocarse en una línea tal que en cada arreglo debe ocurrir P _{1 mientras que P}₄ y P ₅ no no ocurrir Encuentre el número de tales arreglos posibles.

Solución:

Dado, necesitamos organizar 5 personas de 10 personas de manera que en cada arreglo P ₁ debe ocurrir mientras que P ₄ y P ₅ no ocurren.

Aquí, deberíamos elegir P ₁ cada vez, así que ahora, elegimos 4 personas de 9 personas.

De esas 9 personas, no necesitamos elegir P ₄ y P ₅ , por lo que esto se puede hacer de $^7C_4$ varias maneras.

Por lo tanto, número de selecciones = $^7C_4$

¡Y se pueden organizar 5 personas en 5! maneras. asi que,

Número total de formas = $^7C_4.5!$

⇒ 4200.

Por lo tanto, el número de arreglos posibles es 4200.

Pregunta 3: ¿Cuántas palabras, con o sin significado, se pueden formar a partir de las letras de la palabra “LUNES” suponiendo que no se repite ninguna letra? si

(i) Se utilizan 4 letras a la vez.

Solución:

Dado, palabra de seis letras «LUNES».

Se utilizan 4 letras a la vez de 6 letras. esto se puede hacer de $^6C_4$ maneras.

¡Estas cuatro letras se pueden organizar en 4! maneras.

Por lo tanto, número total de formas = $^6C_4.4!$

⇒ 360.

(ii) Todas las letras se utilizan a la vez.

Solución:

Dado, palabra de seis letras «LUNES».

Se utilizan 6 letras a la vez de 6 letras. esto se puede hacer de $^6C_6$ maneras.

¡Estas 6 letras se pueden organizar en 6! maneras.

Por lo tanto, Número total de vías = $^6C_6.6!$

⇒ 1 × 720 = 720

(iii) Se utilizan todas las letras, pero la primera letra es una vocal.

Solución:

Dado, palabra de seis letras «LUNES».

Todas las letras se usan a la vez, pero la primera letra es la vocal,

El número de vocales en la palabra «LUNES» es 2. Entonces, primero elegimos una vocal de estas dos de $^2C_1$ maneras.

Las 5 letras restantes de 5 letras. Esto se puede hacer de $^5C_5$ maneras.

Número de arreglos que se pueden hacer para que estas 5 letras sean 5!.

Por lo tanto, número total de formas = $^2C_1.^5C_5.5!$

⇒ 2\times1\times120=240.

Pregunta 4: Encuentra el número de permutaciones de n cosas distintas tomadas r juntas, en las que 3 cosas particulares deben ocurrir juntas.

Solución:

Dado, Número de permutaciones de n cosas distintas tomando r juntas y 3 cosas particulares ya están seleccionadas.

Entonces, ahora el número de formas de elegir (r – 3) cosas de las restantes (n – 3) cosas es,

Esto se puede hacer de $^{n-3}C_{r-3}$ maneras.

Necesitamos encontrar el número de permutaciones, hay un total (r – 2) de cosas considerando 3 cosas particulares como una sola cosa.

¡Estos se pueden organizar en (r – 2)! maneras.

¡Internamente, 3 cosas particulares se pueden organizar en 3! maneras.

Por lo tanto, Número total de permutaciones = $^{n-3}C_{r-3}\times(r-2)!\times3!$

Pregunta 5: ¿Cuántas palabras de cada 3 vocales y 2 consonantes se pueden formar a partir de las letras de la palabra INVOLUTA?

Solución:

La palabra dada es «INVOLUTA».

Número de vocales y consonantes en la palabra son 4 y 4 respectivamente.

El número de formas de elegir 3 vocales de 4 y 2 consonantes de 4 es $^4C_3\times^4C_2$

¡Estas cinco letras se pueden organizar en 5! maneras.

Por lo tanto, Número total de palabras formadas = $^4C_3\times^4C_2\times5!$

⇒ 4 × 6 × 120 = 2880

Pregunta 6: ¿Encuentre el número de permutaciones de n cosas diferentes tomadas r a la vez de modo que dos cosas específicas ocurran juntas?

Solución:

Dado, el número de permutaciones de n cosas diferentes tomadas r a la vez y dos cosas específicas ocurren juntas.

Entonces, ahora elegimos (r – 2) cosas de las (n – 2) cosas restantes.

Esto se puede hacer de $^{n-2}C_{r-2}$ maneras.

Necesitamos encontrar el número de permutaciones, hay un total (r – 1) de cosas considerando 2 cosas específicas como una sola cosa.

¡Estos se pueden organizar en (r – 1)! maneras.

¡Internamente, 2 cosas particulares se pueden organizar en 2! maneras.

Por lo tanto, Número total de permutaciones = $^{n-2}C_{r-2}\times(r-1)!\times2!$

⇒ $2(r - 1)\times ^{n-2}C_{r-2}\times(r-2)!$

⇒ $2(r - 1)\times ^{n-2}P_{r-2}$

Pregunta 7: Encuentre el número de formas en que: (a) una selección (b) un arreglo, de cuatro letras puede hacerse a partir de las letras de la palabra ‘PROPORCIÓN’.

Solución:

La palabra dada es ‘PROPORCIÓN’

hay 10 letras en esta palabra y principalmente ‘OOO’, ‘PP’, ‘RR’, ‘I’, ‘T’, ‘N’.

(a) Aquí necesitamos seleccionar 4 letras de 10 letras. pero necesitamos considerar algunos casos.

3 letras iguales y 1 letra distinta

2 letras iguales y 2 letras distintas

2 letras iguales de tipo I y 2 letras iguales de otro tipo.

todas las letras distintas.

consideremos,

caso-1 : 3 iguales y 1 distinto

aquí encontramos que sólo una 3 letras iguales en la palabra (‘OOO’).

Entonces, elegir 1 letra distinta de las 5 letras distintas restantes es $^5C_1$

⇒ 5 vías.

caso-2 : 2 letras iguales y 2 letras distintas.

Aquí, encontramos que 3 caracteres tienen 2 letras iguales, el número de formas de elegir 1 letra de 3 es $^3C_1$

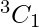
Y el número de formas de elegir 2 letras distintas de las 5 letras restantes es $^5C_2$

⇒ $^3C_1\times ^5C_2=30$ maneras.

caso-3 : 2 letras iguales de tipo I y 2 letras iguales de otro tipo.

Aquí, encontramos que 3 caracteres tienen 2 letras iguales, el número de formas de elegir 2 letras de 3 es $^3C_2$

⇒ 3 formas

Caso-4 : todas las letras distintas.

Aquí, tenemos 6 letras diferentes, el número de formas de elegir 4 letras de 6 es $^6C_4$

⇒ 15 vías.

Por lo tanto, el número total de vías es la suma del número de vías en todos los casos.

⇒ 5+30+3+15=53 vías.

(b) Aquí necesitamos organizar 4 letras de 10 letras, aquí los casos serán los mismos que en la selección, pero organizamos las letras dadas en cada caso.

caso-1 : Número de formas de seleccionar 3 letras iguales y 1 distinta es 5.

El número de formas de organizar es similar a organizar a las n personas en n lugares donde r lugares son iguales = $\frac{n!}{r!}$

Del mismo modo, la disposición de 4 letras donde 3 son iguales es $\frac{4!}{3!}$

número total de formas son $5\times \frac{4!}{3!} =20$

caso-2: Número de formas de seleccionar 2 letras iguales y 2 letras distintas es 30 formas.

formas numéricas de ordenarlos es $\frac{4!}{2!}$

El número total de formas es $30\times \frac{4!}{2!} =360$

case-3 : Número de formas de seleccionar 2 letras iguales y 2 letras iguales es 3 formas.

El número de formas de organizarlos es $\frac{4!}{2!\times2!}$

El número total de formas es $3\times \frac{4!}{2!\times2!} =18$

Caso-4 : El número de formas de seleccionar 4 letras distintas es 15 formas.

número de maneras de organizarlos es 4!

¡El número total de formas es 15 × 4! = 360

considerando todos los casos, el número total de formas es la suma de todas las formas de todos los casos

⇒ 20+360+18+360 = 758 formas.

Pregunta 8: ¿Cuántas palabras se pueden formar tomando 4 letras a la vez de las letras de la palabra ‘MORADABAD’?

Solución:

La palabra dada es ‘MORADABAD’

Hay 10 letras en esta palabra y principalmente ‘AAA’, ‘DD’, ‘M’, ‘R’, ‘B’, ‘O’.

(a) Aquí necesitamos seleccionar 4 letras de 10 letras. pero necesitamos considerar algunos casos.

3 letras iguales y 1 letra distinta

2 letras iguales y 2 letras distintas

2 letras iguales de tipo I y 2 letras iguales de otro tipo.

todas las letras distintas.

consideremos,

caso-1 : 3 iguales y 1 distinto

aquí encontramos que sólo una 3 letras iguales en la palabra (‘AAA’).

Entonces, elegir 1 letra distinta de las 5 letras distintas restantes es $^5C_1$

El número de formas de ordenarlos es $\frac{4!}{3!}$

⇒ $5\times\frac{4!}{3!}=20$ maneras.

caso-2 : 2 letras iguales y 2 letras distintas.

Aquí, encontramos que 2 caracteres tienen 2 letras iguales, el número de formas de elegir 1 letra de 2 es $^2C_1$

Y el número de formas de elegir 2 letras distintas de las 5 letras restantes es $^5C_2$

El número de formas de ordenarlos es $\frac{4!}{2!}$

⇒ $^2C_1\times ^5C_2\times\frac{4!}{2!}=240$ maneras.

caso-3 : 2 letras iguales de tipo I y 2 letras iguales de otro tipo.

Aquí, encontramos que 2 caracteres tienen 2 letras iguales, el número de formas de elegir 2 letras de 2 es $^2C_2$

El número de formas de ordenarlos es $\frac{4!}{2!\times2!}$

⇒ $^2C_2\times\frac{4!}{2!\times2!}=6$ formas

Caso-4 : todas las letras distintas.

Aquí, tenemos 6 letras diferentes, el número de formas de elegir 4 letras de 6 es $^6C_4$

¡El número de formas de organizarlos es 4!

⇒ $^6C_4\times4!= 360$ maneras.

Por lo tanto, el número total de vías es la suma del número de vías en todos los casos.

⇒ 20+240+6+360 = 626 formas.

Pregunta 9: Un hombre de negocios organiza una cena para 21 invitados. Tiene 2 mesas redondas con capacidad para 15 y 6 personas cada una. ¿De cuántas maneras puede ordenar a los invitados?

Solución:

Dado, un hombre de negocios organiza cenas para 21 invitados, donde 2 mesas redondas tienen capacidad para 16 y 6 personas.

Entonces, elegir 15 invitados de 21 para acomodar en una mesa de $^{21}C_{15}$ maneras.

¡Esos 15 invitados se pueden organizar en sí mismos en (15 – 1)! maneras. porque es una mesa redonda.

Entonces, ¡necesitamos mantener un invitado fijo y organizar los 14 invitados restantes = (15 – 1)! = 14!.

Después de acomodar a 15 invitados en una mesa, acomodar a los 6 invitados restantes de 6 en otra mesa de $^6C_6$ maneras.

¡Esos 6 invitados se pueden organizar en (6 – 1)! = 5! maneras.

Número total de formas = $^{21}C_{15}\times^6C_6\times14!\times5!=^{21}C_{15}\times14!\times5!$

Pregunta 10: Encuentra el número de combinaciones y permutaciones de 4 letras tomadas de la palabra ‘EXAMINACIÓN’.

Solución:

La palabra dada es ‘EXAMEN’

Hay 10 letras en esta palabra y principalmente ‘AA’, ‘NN’, ‘II’, ‘E’, ‘X’, ‘O’, ‘M’, ‘T’.

(a) Aquí necesitamos seleccionar 4 letras de 10 letras. pero necesitamos considerar algunos casos.

2 letras iguales y 2 letras distintas

2 letras iguales de tipo I y 2 letras iguales de otro tipo.

todas las letras distintas.

consideremos,

caso-1 : 2 letras iguales y 2 letras distintas.

Aquí, encontramos que 3 caracteres tienen 2 letras iguales, el número de formas de elegir 1 letra de 3 es $^3C_1$

Y el número de formas de elegir 2 letras distintas de las 7 letras restantes es $^7C_2$

El número de formas de ordenarlos es $\frac{4!}{2!}$

⇒ $^3C_1\times ^7C_2\times\frac{4!}{2!}=756$ maneras.

caso-2 : 2 letras iguales de tipo I y 2 letras iguales de otro tipo.

Aquí, encontramos que 3 caracteres tienen 2 letras iguales, el número de formas de elegir 2 letras de 3 es $^3C_2$

El número de formas de ordenarlos es $\frac{4!}{2!\times2!}$

⇒ $^3C_2\times\frac{4!}{2!\times2!}=18$ formas

Caso-3 : todas las letras distintas.

Aquí, tenemos 6 letras diferentes, el número de formas de elegir 4 letras de 8 es $^8C_4$

¡El número de formas de organizarlos es 4!

⇒ $^8C_4\times4!= 1680$ maneras.

Por lo tanto, el número total de vías es la suma del número de vías en todos los casos.

⇒ 756+18+1680 = 2454 vías.

Pregunta 11: Se organiza una fiesta de té para 16 personas a lo largo de dos lados de una mesa larga con 8 sillas en cada lado. Cuatro personas desean sentarse en un lado en particular y dos en otro lado. ¿De cuántas maneras se pueden sentar?

Solución:

Dado, Se organiza una fiesta de té de 16 personas a lo largo de dos lados de una mesa larga con 8 sillas en cada lado.

Sean dos lados lado A, lado B.

Además, 4 personas desean sentarse en el lado A y 2 personas en el lado B.

Los asientos restantes en el lado A y el lado B son 4, 6 respectivamente.

Ahora, elijamos 4 personas de las 10 restantes en el lado A.

Esto se puede hacer de $^{10}C_4$ maneras.

Además, eligiendo 6 personas de las 6 restantes en el lado B.

Esto se puede hacer de $^6C_6$ maneras.

¡Ahora, 8 personas en cada lado se pueden organizar en 8! maneras.

Por lo tanto, número total de formas = $^{10}C_4\times^6C_6\times8!\times8!$

⇒ $^{10}C_4\times(8!)^2$

Publicación traducida automáticamente

Artículo escrito por srinivasteja18 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1: ¿Cuántas palabras diferentes, cada una con 2 vocales y 3 consonantes, se pueden formar con 5 vocales y 17 consonantes?

Pregunta 2: Hay 10 personas nombradas P 1 ,P 2 ,P 3 ….P 10 de 10 personas, 5 personas deben colocarse en una línea tal que en cada arreglo debe ocurrir P 1 mientras que P 4 y P 5 no no ocurrir Encuentre el número de tales arreglos posibles.

Pregunta 3: ¿Cuántas palabras, con o sin significado, se pueden formar a partir de las letras de la palabra “LUNES” suponiendo que no se repite ninguna letra? si

(i) Se utilizan 4 letras a la vez.

(ii) Todas las letras se utilizan a la vez.

(iii) Se utilizan todas las letras, pero la primera letra es una vocal.

Pregunta 4: Encuentra el número de permutaciones de n cosas distintas tomadas r juntas, en las que 3 cosas particulares deben ocurrir juntas.

Pregunta 5: ¿Cuántas palabras de cada 3 vocales y 2 consonantes se pueden formar a partir de las letras de la palabra INVOLUTA?

Pregunta 6: ¿Encuentre el número de permutaciones de n cosas diferentes tomadas r a la vez de modo que dos cosas específicas ocurran juntas?

Pregunta 7: Encuentre el número de formas en que: (a) una selección (b) un arreglo, de cuatro letras puede hacerse a partir de las letras de la palabra ‘PROPORCIÓN’.

Pregunta 8: ¿Cuántas palabras se pueden formar tomando 4 letras a la vez de las letras de la palabra ‘MORADABAD’?

Pregunta 9: Un hombre de negocios organiza una cena para 21 invitados. Tiene 2 mesas redondas con capacidad para 15 y 6 personas cada una. ¿De cuántas maneras puede ordenar a los invitados?

Pregunta 10: Encuentra el número de combinaciones y permutaciones de 4 letras tomadas de la palabra ‘EXAMINACIÓN’.

Pregunta 11: Se organiza una fiesta de té para 16 personas a lo largo de dos lados de una mesa larga con 8 sillas en cada lado. Cuatro personas desean sentarse en un lado en particular y dos en otro lado. ¿De cuántas maneras se pueden sentar?

Deja una respuesta Cancelar la respuesta

Pregunta 2: Hay 10 personas nombradas P ₁ ,P ₂ ,P ₃ ….P ₁₀ de 10 personas, 5 personas deben colocarse en una línea tal que en cada arreglo debe ocurrir P _{1 mientras que P}₄ y P ₅ no no ocurrir Encuentre el número de tales arreglos posibles.