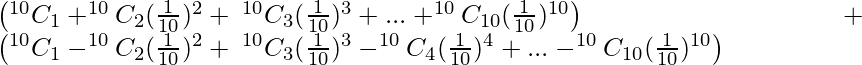Pregunta 1. Usando el teorema del binomio, escriba las expresiones de lo siguiente:
(yo) (2x + 3y) 5
Solución:
Usando el teorema del binomio, tenemos,
(2x + 3y) 5 = 5 C 0 (2x) 5 (3y) 0 + 5 C 1 (2x) 4 (3y) 1 + 5 C 2 (2x) 3 (3y) 2 + 5 C 3 (2x) 2 (3y) 3 + 5 C 4 (2x) 1 (3y) 4 + 5 C 5 (2x) 0 (3y) 5
= 32x 5 + 5 (16x 4 ) (3y) + 10 (8x 3 ) (9y) 2 + 10 (4x) 2 (27y) 3 + 5 (2x) (81y 4 ) + 243 y 5
= 32x 5 + 240x 4 y + 720x 3 y 2 + 1080x 2 y 3 + 810xy 4 + 243y 5
(ii) (2x – 3y) 4
Solución:
Usando el teorema del binomio, tenemos,
(2x – 3y) 4 = 4 C 0 (2x) 4 (3y) 0 – 4 C 1 (2x) 3 (3y) 1 + 4 C 2 (2x) 2 (3y) 2 – 4 C 3 (2x) 1 (3y) 3 + 4 C 4 (2x) 0 (3y) 4
= 16x 4 – 4 (8x 3 ) (3y) + 6 (4x 2 ) (9y 2 ) – 4 (2x) (27y 3 ) + 81y 4
= 16x 4 – 96x 3 y + 216x 2 y 2 – 216xy 3 + 81y 4
(iii) (x – 1/x) 6
Solución:
Usando el teorema del binomio, tenemos,
(x – 1/x) 6 = 6 C 0 x 6 (1/x) 0 – 6 C 1 x 5 (1/x) 1 + 6 C 2 x 4 (1/x) 2 – 6 C 3 x 3 (1/x) 3 + 6 C 4 x 2 (1/x) 4 – 6 C 5 x 1 (1/x) 5 + 6 C 6 (1/x) 6
= x 6 – 6x 5 (1/x) + 15x 4 (1/x 2 ) – 20 x 3 (1/x 3 ) + 15x 2 (1/x 4 ) – 6x (1/x 5 ) + 1/ x6 _
= x 6 – 6x 4 + 15x 2 – 20 + 15/x 2 – 6/x 4 + 1/x 6
(iv) (1 – 3x) 7
Solución:
Usando el teorema del binomio, tenemos,
(1 – 3x) 7 = 7 C 0 (3x) 0 – 7 C 1 (3x) 1 + 7 C 2 (3x) 2 – 7 C 3 (3x) 3 + 7 C 4 (3x) 4 – 7 C 5 (3x) 5 + 7 C 6 (3x) 6 – 7 C 7 (3x) 7
= 1 – 7 (3x) + 21 (9x) 2 – 35 (27x 3 ) + 35 (81x 4 ) – 21 (243x 5 ) + 7 (729x 6 ) – 2187(x 7 )
= 1 – 21x + 189x 2 – 945x 3 + 2835x 4 – 5103x 5 + 5103x 6 – 2187x 7
(v) (hacha – b/x) 6
Solución:
Usando el teorema del binomio, tenemos,
(hacha – b/x)^6 =
=
=
(vi) 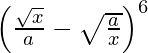
Solución:
Usando el teorema del binomio, tenemos,
=
(vii) ![Rendered by QuickLaTeX.com \left( \sqrt[3]{x} - \sqrt[3]{a} \right)^6](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0595efec6736fe18f6d2e87d28ef3007_l3.png)
Solución:
Usando el teorema del binomio, tenemos,
=
(viii) (1 + 2x – 3x 2 ) 5
Solución:
Usando el teorema del binomio, tenemos,
(1 + 2x – 3x 2 ) 5 = 5 C 0 (1 + 2x) 5 (3x 2 ) 0 – 5 C 1 (1 + 2x) 4 (3x 2 ) 1 + 5 C 2 (1 + 2x) 3 ( 3x 2 ) 2 – 5 C 3 (1 + 2x) 2 (3x 2 ) 3 + 5 C 4 (1 + 2x) 1 (3x 2 ) 4 –5 C 5 (1 + 2x) 0 (3x 2 ) 5
= (1 + 2x) 5 – 5(1 + 2x) 4 (3x 2 ) + 10 (1 + 2x) 3 (9x 4 ) – 10 (1 + 2x) 2 (27x 6 ) + 5 (1 + 2x) (81×8 ) – 243×10
= 5 C 0 (2x) 0 + 5 C 1 (2x) 1 + 5 C 2 (2x) 2 + 5 C 3 (2x) 3 + 5 C 4 (2x) 4 + 5 C 5 (2x) 5 – 15x 2 [ 4 C 0 (2x) 0 + 4 C 1 (2x) 1 + 4 C 2 (2x) 2 +4 C 3 (2x) 3 + 4 C 4 (2x) 4 ] + 90x 4 [1 + 8x 3 + 6x + 12x 2 ] – 270x 6 (1 + 4x 2 + 4x) + 405x 8 + 810x 9 – 243x 10
= 1 + 10x + 40x 2 + 80x 3 + 80x 4 + 32x 5 – 15x 2 – 120x 3 – 360 4 – 480x 5 – 240x 6 + 90x 4 + 720x 7 + 540x 5 + 1080x 6 – 270x 6 – 1080x 8 – 1080x 7 + 405x 8 + 810x 9 – 243x 10
= 1 + 10x + 25x 2 – 40x 3 – 190x 4 + 92x 5 + 570x 6 – 360x 7 – 675x 8 + 810x 9 – 243x 10
(ix) 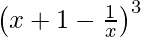
Solución:
Usando el teorema del binomio, tenemos,
(x + 1 – 1/x) 3 = 3 C 0 (x + 1) 3 (1/x) 0 – 3 C 1 (x + 1) 2 (1/x) 1 + 3 C 2 (x + 1 ) 1 (1/x) 2 – 3 C 3 (x + 1) 0 (1/x) 3
=
=
=
=
(x) (1 – 2x + 3x 2 ) 3
Solución:
Usando el teorema del binomio, tenemos,
(1 – 2x + 3 x 2 ) 3 = 3 C 0 (1 – 2x) 3 + 3 C 1 (1 – 2x) 2 (3x 2 ) + 3 C 2 (1 – 2x)(3x 2 ) 2 + 3 C 3 (3x 2 ) 3
= (1 – 2x) 3 + 9x 2 (1 – 2x) 2 + 27x 4 (1 – 2x) + 27x 6
= 1 – 8x 3 + 12x 2 – 6x + 9x 2 (1 + 4x 2 – 4x) + 27x 4 – 54x 5 + 27x 6
= 1 – 8x 3 + 12x 2 – 6x + 9x 2 + 36x 4 – 36x 3 + 27x 4 – 54x 5 + 27x 6
= 1 – 6x + 21x 2 – 44x 3 + 63x 4 – 54x 5 + 27x 6
Pregunta 2. Evalúa lo siguiente:
(i) 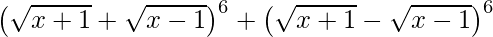
Solución:
Usando el teorema del binomio, tenemos,
=
= 2 [(x + 1) 3 + 15(x + 1) 2 (x – 1) + 15(x + 1)(x – 1 ) 2 + (x – 1 ) 3 ]
= 2 [x 3 + 1 + 3x + 3 x 2 + 15( x 2 + 2x + 1)(x – 1) + 15(x + 1)( x 2 + 1 – 2x) + x 3 – 1 + 3x – 3×2 ]
= 2 [2 x 3 + 6x + 15 x 3 – 15 x 2 + 30 x 2 – 30x + 15x – 15 + 15 x 3 + 15 x 2 – 30 x 2 – 30x + 15x + 15]
= 2 [ 32×3 – 24x]
= 16x [4x 2 – 3]
(ii) 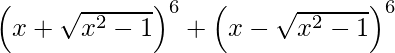
Solución:
Usando el teorema del binomio, tenemos,
= 2 [x 6 + 15 x 4 ( x 2 – 1) + 15 x 2 ( x 2 – 1 ) 2 + ( x 2 – 1 ) 3 ]
= 2 [x 6 + 15 x 6 – 15 x 4 + 15 x 2 ( x 4 – 2 x 2 + 1) + ( x 6 – 1 + 3 x 2 – 3 x 4 )]
= 2 [x 6 + 15 x 6 – 15 x 4 + 15 x 6 – 30 x 4 + 15 x 2 + x 6 – 1 + 3 x 2 – 3 x 4 ]
= 64 x 6 – 96 x 4 + 36 x 2 – 2
(iii) 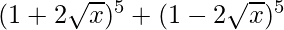
Solución:
Usando el teorema del binomio, tenemos,
= 2 [ 5 C 0 (2√x) 0 + 5 C 2 (2√x) 2 + 5 C 4 (2√x) 4 ]
= 2 [1 + 10 (4x) + 5 (16x 2 )]
= 2 [1 + 40x + 80x 2 ]
(iv) 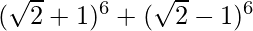
Solución:
Usando el teorema del binomio, tenemos,
= 2 [ 6 C 0 (√2) 6 + 6 C 2 (√2) 4 + 6 C 4 (√2) 2 + 6 C 6 (√2) 0 ]
= 2 [8 + 15 (4) + 15 (2) + 1]
= 2 [99]
= 198
(v) 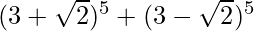
Solución:
Usando el teorema del binomio, tenemos,
= 2 [ 5 C 1 (3 4 ) (√2) 1 + 5 C 3 (3 2 ) (√2) 3 + 5 C 5 (3 0 ) (√2) 5 ]
= 2 [5 (81) (√2) + 10 (9) (2√2) + 4√2]
= 2√2 (405 + 180 + 4)
= 1178√2
(vi) 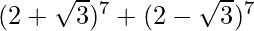
Solución:
Usando el teorema del binomio, tenemos,
= 2 [ 7 C 0 (2 7 ) (√3) 0 + 7 C 2 (2 5 ) (√3) 2 + 7 C 4 (2 3 ) (√3) 4 + 7 C 6 (2 1 ) ( √3) 6 ]
= 2 [128 + 21 (32)(3) + 35(8)(9) + 7(2)(27)]
= 2 [128 + 2016 + 2520 + 378]
= 2 [5042]
= 10084
(vii) 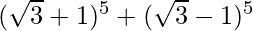
Solución:
Usando el teorema del binomio, tenemos,
= 2 [ 5 C 1 (√3) 4 + 5 C 3 (√3) 2 + 5 C 5 (√3) 0 ]
= 2 [5 (9) + 10 (3) + 1]
= 2 [76]
= 152
(viii) (0,99) 5 + (1,01) 5
Solución:
Usando el teorema del binomio, tenemos,
(0,99) 5 + (1,01) 5 = (1 – 0,01) 5 + (1 + 0,01) 5
= 2 [ 5 C 0 (0.01) 0 + 5 C 2 (0.01) 2 + 5 C 4 (0.01) 4 ]
= 2 [1 + 10 (0,0001) + 5 (0,00000001)]
= 2 [1.00100005]
= 2.0020001
(ix) 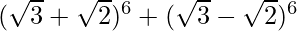
Solución:
Usando el teorema del binomio, tenemos,
= 2 [ 6 C 1 (√3) 5 (√2) 1 + 6 C 3 (√3) 3 (√2) 3 + 6 C 5 (√3) 1 (√2) 5 ]
= 2 [6 (9√3) (√2) + 20 (3√3) (2√2) + 6 (√3) (4√2)]
= 2 [√6 (54 + 120 + 24)]
= 396 √6
(X) 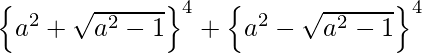
Solución:
Usando el teorema del binomio, tenemos,
= 2[ un 8 + 6 un 4 (un 2 – 1) + ( un 2 – 1 ) 2 ]
= 2[un 8 + 6 un 6 – 6 un 4 + un 4 + 1 – 2 un 2 ]
= 2 a 8 + 12 a 6 – 10 a 4 – 4 a 2 + 2
Pregunta 3. Encuentra (a + b) 4 – (a – b) 4 . Por lo tanto, evalúe (√3 + √2) 4 – (√3 – √2) 4 .
Solución:
Se nos da,
(a + b) 4 – (a – b) 4 = 2 [ 4 C 1 un 3 segundo 1 + 4 C 3 un 1 segundo 3 ]
= 2 [4a 3 b + 4ab 3 ]
= 8 (a 3 b + ab 3 )
Ahora,
(√3 + √2) 4 – (√3 – √2) 4 = 8 (a 3 b + ab 3 )
= 8 [(√3) 3 (√2) + (√3) (√2) 3 ]
= 8 [(3√6) + (2√6)]
= 8 (5√6)
= 40√6
Pregunta 4. Encuentra (x + 1) 6 + (x – 1) 6 . Por lo tanto, o de lo contrario evaluar (√2 + 1) 6 + (√2 – 1) 6 .
Solución:
Se nos da,
(x + 1) 6 + (x – 1) 6 = 2 [ 6 C 0 x 6 + 6 C 2 x 4 + 6 C 4 x 2 + 6 C 6 x 0 ]
= 2 [x 6 + 15x 4 + 15x 2 + 1]
Ahora,
(√2 + 1) 6 + (√2 – 1) 6
Así que considera, x = √2 entonces obtenemos,
(√2 + 1) 6 + (√2 – 1) 6 = 2 [x 6 + 15x 4 + 15x 2 + 1]
= 2 [(√2) 6 + 15 (√2) 4 + 15 (√2) 2 + 1]
= 2 [8 + 15 (4) + 15 (2) + 1]
= 2 [8 + 60 + 30 + 1]
= 198
Pregunta 5. Usando el teorema del binomio, evalúe cada uno de los siguientes:
(yo) (96) 3
Solución:
Al expresar la expresión dada como dos entidades distintas y aplicar el teorema del binomio, obtenemos,
(96) 3 = (100 – 4) 3
= 3 C 0 (100) 3 (4) 0 – 3 C 1 (100) 2 (4) 1 + 3 C 2 (100) 1 (4) 2 – 3 C 3 (100) 0 (4) 3
= 1000000 – 120000 + 4800 – 64
= 884736
(ii) (102) 5
Solución:
Al expresar la expresión dada como dos entidades distintas y aplicar el teorema del binomio, obtenemos,
(102) 5 = (100 + 2) 5
= 5 C 0 (100) 5 (2) 0 + 5 C 1 (100) 4 (2) 1 + 5 C 2 (100) 3 (2) 2 + 5 C 3 (100) 2 (2) 3 + 5 C 4 (100) 1 (2) 4 + 5 C 5 (100) 0 (2) 5
= 10000000000 + 1000000000 + 40000000 + 800000 + 8000 + 32
= 11040808032
(iii) (101) 4
Solución:
Al expresar la expresión dada como dos entidades distintas y aplicar el teorema del binomio, obtenemos,
(101) 4 = (100 + 1) 4
= 4 C 0 (100) 4 + 4 C 1 (100) 3 + 4 C 2 (100) 2 + 4 C 3 (100) 1 + 4 C 4 (100) 0
= 100000000 + 4000000 + 60000 + 400 + 1
= 104060401
(iv) (98) 5
Solución:
Al expresar la expresión dada como dos entidades distintas y aplicar el teorema del binomio, obtenemos,
(98) 5 = (100 – 2) 5
= 5 C 0 (100) 5 (2) 0 – 5 C 1 (100) 4 (2) 1 + 5 C 2 (100) 3 (2) 2 – 5 C 3 (100) 2 (2) 3 + 5 C 4 (100) 1 (2) 4 – 5 C 5 (100) 0 (2) 5
= 10000000000 – 1000000000 + 40000000 – 800000 + 8000 – 32
= 9039207968
Pregunta 6. Usando el teorema del binomio, demuestra que 2 3n – 7n – 1 es divisible por 49, donde n ∈ N.
Solución:
Se nos da,
2 3n – 7n – 1 = 8n – 7n – 1
= (1 + 7) n – 7n – 1
= norte C 0 + norte C 1 (7) 1 + norte C 2 (7) 2 + norte C 3 (7) 3 + norte C 4 (7) 2 + norte C 5 (7) 1 + .… + norte C norte (7) norte – 7n – 1
= 1 + 7n + 7 2 [ norte C 2 + norte C 3 (7 1 ) + norte C 4 (7 2 ) + … + norte C norte (7) n -2 ] – 7n – 1
= 49 [ n C 2 + n C 3 (7 1 ) + n C 4 (7 2 ) + … + n C n (7) n-2 ] , que es divisible por 49.
Por lo tanto, 2 3n – 1 – 7n es divisible por 49.
Por lo tanto probado.
Pregunta 7. Usando el teorema del binomio, demuestra que 3 2n+2 – 8n – 9 es divisible por 64, donde n ∈ N.
Solución:
Se nos da,
3 2n+2 – 8n – 9 = 3 2(n+1) – 8n – 9
= 9 n+1 – 8n – 9
= (1 + 8) n+1 – 8n – 9
= n+1 C 0 + n+1 C 1 (8) 1 + n+1 C 2 (8) 2 + n+1 C 3 (8) 3 + n+1 C 4 (8) 2 + n+1 C 5 (8) 1 + .… + n+1 C n+1 (8) n+1 – 8n – 9
= 1 + 8(n+1) + 8 2 [ n+1 C 2 + n+1 C 3 (8 1 ) + n+1 C 4 (8 2 ) + … + n+1 C n+1 (8 ) n-1 ] – 8n – 9
= 8n + 9 + 64 [ n+1 C 2 + n+1 C 3 (8 1 ) + n+1 C 4 (8 2 ) + … + n+1 C n+1 (8) n-1 ] – 8n-9
= 64 [ n+1 C 2 + n+1 C 3 (8 1 ) + n+1 C 4 (8 2 ) + … + n+1 C n+1 (8) n-1 ], que es divisible por 64.
Por lo tanto, 3 2n+2 – 8n – 9 es divisible por 64.
Por lo tanto probado.
Pregunta 8. Si n es un entero positivo, prueba que 3 3n – 26n – 1 es divisible por 676.
Solución:
Se nos da,
3 3n – 26n – 1 = (3 3 ) n – 26n – 1
= 27n – 26n – 1
= (1 + 26) n – 26n – 1
= norte C 0 + norte C 1 (26) 1 + norte C 2 (26) 2 + norte C 3 (26) 3 + norte C 4 (26) 2 + norte C 5 (26) 1 + .… + norte C norte (26) norte – 26n – 1
= 1 + 26n + 26 2 [ norte C 2 + norte C 3 (26 1 ) + norte C 4 (26 2 ) + … + norte C norte (26) n -2 ] – 26n – 1
= 676 [ n C 2 + n C 3 (26 1 ) + n C 4 (26 2 ) + … + n C n (26) n-2 ] , que es divisible por 676.
Por lo tanto, 3 3n – 26n – 1 es divisible por 676.
Por lo tanto probado.
Pregunta 9. Usando el teorema del binomio, indica cuál es mayor (1.1) 10000 o 1000.
Solución:
Tenemos,
(1,1) 10000 = (1 + 0,1) 10000
= 10000 C 0 + 10000 C 1 (0.1) 1 + 10000 C 2 (0.1) 2 + .… + 10000 C 10000 (0.1) 10000
= 1 + (10000) (0.1) + otros términos positivos
= 1 + 1000 + otros términos positivos
= 1001 + otros términos positivos
Por lo tanto, (1.1) 10000 es mayor que 1000.
Pregunta 10. Usando el teorema del binomio, determine qué número es mayor, (1.2) 4000 o 800.
Solución:
Tenemos,
(1,2) 4000 = (1 + 0,2) 4000
= 4000 C 0 + 4000 C 1 (0,2) 1 + 4000 C 2 (0,2) 2 + .… + 4000 C 4000 (0,2) 4000
= 1 + (4000) (0.2) + otros términos positivos
= 1 + 800 + otros términos positivos
= 801 + otros términos positivos
Por lo tanto, (1.2) 4000 es mayor que 800.
Pregunta 11. Encuentra el valor de (1.01) 10 + (1−0.01) 10 correcto con 7 decimales.
Solución:
Tenemos,
(1,01) 10 + (1−0,01) 10 = (1+0,01) 10 + (1−0,01) 10
=
=
=
=
= 2.0090042
Pregunta 12. Demuestra que 2 4n+4 − 15n − 16, donde n ∈ N es divisible por 225.
Solución:
Tenemos,
2 4n+4 − 15n − 16 = 2 4(n+1) − 15n − 16
= 16 n+1 − 15n − 16
= (1 + 15) n+1 − 15n − 16
= n+1 C 0 + n+1 C 1 (15) 1 + n+1 C 2 (15) 2 + n+1 C 3 (15) 3 + n+1 C 4 (15) 2 + n+1 C 5 (15) 1 + .… + n+1 C n+1 (15) n+1 − 15n − 16
= 1 + 15(n+1) + 15 2 [ n+1 C 2 + n+1 C 3 (15 1 ) + n+1 C 4 (15 2 ) + … + n+1 C n+1 (15 ) n-1 ] – 15n – 16
= 15n + 16 + 225 [ n+1 C 2 + n+1 C 3 (15 1 ) + n+1 C 4 (15 2 ) + … + n+1 C n+1 (15) n-1 ] – 15n – 16
= 225 [ n+1 C 2 + n+1 C 3 (15 1 ) + n+1 C 4 (15 2 ) + … + n+1 C n+1 (15) n-1 ] , que es divisible por 225.
Por lo tanto, 2 4n+4 − 15n − 16 es divisible por 225.
Por lo tanto probado.
Publicación traducida automáticamente
Artículo escrito por gurjotloveparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
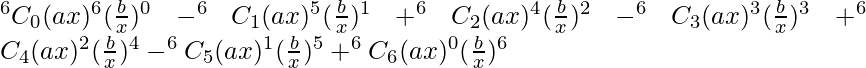

![Rendered by QuickLaTeX.com \left( \sqrt[3]{x} - \sqrt[3]{a} \right)^6 = ^{6}{}{C}_0 (\sqrt[3]{x} )^6 (\sqrt[3]{a} )^0 -^{6}{}{C}_1 (\sqrt[3]{x} )^5 (\sqrt[3]{a} )^1 +^{6}{}{C}_2 (\sqrt[3]{x} )^4 (\sqrt[3]{a} )^2 -^{6}{}{C}_3 (\sqrt[3]{x} )^3 (\sqrt[3]{a} )^3 +^{6}{}{C}_4 (\sqrt[3]{x} )^2 (\sqrt[3]{a} )^4 -^{6}{}{C}_5 (\sqrt[3]{x} )^1 (\sqrt[3]{a} )^5 + ^{6}{}{C}_6 (\sqrt[3]{x} )^0 (\sqrt[3]{a} )^6](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-de18aa60648259abb36fdbf5d0866dec_l3.png)
![Rendered by QuickLaTeX.com 2[ ^{6}{}{C}_0 (\sqrt{x + 1} )^6 (\sqrt{x - 1} )^0 + ^{6}{}{C}_2 (\sqrt{x + 1} )^4 (\sqrt{x - 1} )^2 +^{6}{}{C}_4 (\sqrt{x + 1} )^2 (\sqrt{x - 1} )^4 + ^{6}{}{C}_6 (\sqrt{x + 1} )^0 (\sqrt{x - 1} )^6 ]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ec7297ec095720948ee84f73721fc9f1_l3.png)
![Rendered by QuickLaTeX.com (x + \sqrt{x^2 - 1} )^6 + (x - \sqrt{x^2 - 1} )^6 = 2[ ^ {6}{}{C}_0 x^6 (\sqrt{x^2 - 1} )^0 +^{6}{}{C}_2 x^4 (\sqrt{x^2 - 1} )^2 +^{6}{}{C}_4 x^2 (\sqrt{x^2 - 1} )^4 + ^{6}{}{C}_6 x^0 (\sqrt{x^2 - 1} )^6 ]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-69d57ac98243e15175f6cf4cfc03285c_l3.png)
![Rendered by QuickLaTeX.com \left\{ a^2 + \sqrt{a^2 - 1} \right\}^4 + \left\{ a^2 - \sqrt{a^2 - 1} \right\}^4 = 2[ ^{4}{}{C}_0 ( a^2 )^4 (\sqrt{a^2 - 1} )^0 +^{4}{}{C}_2 ( a^2 )^2 (\sqrt{a^2 - 1} )^2 + ^{4}{}{C}_4 ( a^2 )^0 (\sqrt{a^2 - 1} )^4 ]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7ee17f903a56814624aa76b8bba5a1ec_l3.png)