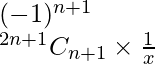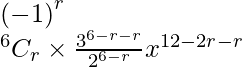Clase 11 Soluciones RD Sharma – Capítulo 18 Teorema del binomio – Ejercicio 18.2

Pregunta 14. Encuentra los términos medios en la expansión de:

(yo) (3x – x ^3/6 ) ⁹

Solución:

Tenemos,

(3x – x ^3/6 ) ⁹ donde, n = 9 (número impar).

Entonces, los términos medios son ((n + 1)/2) = ((9 + 1)/2) = 10/2 = 5 y

((n + 1)/2 + 1) = ((9 + 1)/2 + 1) = (10/2 + 1) = (5 + 1) = 6

Los términos son ^5º y ^6º .

Ahora,

T ₅ = T ₄₊₁

= ⁹ C ₄ (3x) ^9-4 (x ³ /6) ⁴

= $\frac{9×8×7×6}{5×4×3×2×1}×27×9×\frac{x^{17}}{36×36}$

= $\frac{189x^{17}}{8}$

Y, T ₆ = T ₅₊₁

= ⁹ C ₅ (3x) ^9-5 (x ³ /6) ⁵

= $-\frac{9×8×7×6}{5×4×3×2×1}×81×9×\frac{x^{19}}{216×36}$

= $-\frac{21x^{19}}{16}$

(ii) (2x ² – 1/x) ⁷

Solución:

Tenemos,

(2x ² – 1/x) ⁷ donde, n = 7 (número impar).

Entonces los términos medios son ((n + 1)/2) = ((7 + 1)/2) = 8/2 = 4 y

((n + 1)/2 + 1) = ((7 + 1)/2 + 1) = (8/2 + 1) = (4 + 1) = 5

Los términos son ^4º y ^5º .

Ahora,

T4 = T3 ₊₁

= ⁷ C ₃ (2x ² ) ^7-3 (-1/x) ³

= -\frac{7×6×5}{3×2}×16x^8×\frac{1}{x^3}

= − 560 × ⁵

Y, T ₅ = T ₄₊₁

= ⁷ C ₄ (2x ² ) ^7-4 (-1/x) ⁴

= $\frac{7×6×5}{3×2}×8×x^6×\frac{1}{x^4}$

= ^280×2

(iii) (3x – 2/x ² ) ¹⁵

Solución:

Tenemos,

(3x – 2/x ² ) ¹⁵ donde, n = 15 (número impar)

Entonces los términos medios son ((n + 1)/2) = ((15 + 1)/2) = 16/2 = 8 y

((n + 1)/2 + 1) = ((15 + 1)/2 + 1) = (16/2 + 1) = (8 + 1) = 9

Los términos son 8 ^th y 9 ^th .

Ahora,

T ₈ = T ₇₊₁

= ¹⁵ C ₇ (3x) ^15-7 (– 2/x ² ) ⁷

= $-\frac{15×14×13×12×11×10×9}{7×6×5×4×3×2×1}×3^8×2^7×x^{8-14}$

= $\frac{-6435×3^8×2^7}{x^{6}}$

Y, T ₉ = T ₈₊₁

= ¹⁵ C ₈ (3x) ^15-8 (– 2/x ² ) ⁸

= $-\frac{15×14×13×12×11×10×9}{7×6×5×4×3×2×1}×3^7×2^8×x^{7-16}$

= $\frac{6435×3^7×2^8}{x^{9}}$

(iv) (x ⁴ – 1/x ³ ) ¹¹

Solución:

(x ⁴ – 1/x ³ ) ¹¹

Entonces los términos medios son ((n + 1)/2) = ((11 + 1)/2) = 12/2 = 6 y

((n + 1)/2 + 1) = ((11 + 1)/2 + 1) = (12/2 + 1) = (6 + 1) = 7

Los términos son ^6º y ^7º .

Ahora,

T ₆ = T ₅₊₁

= ¹¹ C ₅ (x ⁴ ) ^11-5 (1/x ³ ) ⁵

= $- \frac{11 \times 10 \times 9 \times 8 \times 7}{5 \times 4 \times 3 \times 2} \times \left( x \right)^{24 - 15}$

= ^-462×9

Y, T ₇ = T ₆₊₁

= ¹¹ C ₆ (x ⁴ ) ^11-6 (1/x ³ ) ⁶

= $\frac{11 \times 10 \times 9 \times 8 \times 7}{5 \times 4 \times 3 \times 2} \left( x \right)^{20 - 18}$

= ^462×2

Pregunta 15. Encuentra los términos medios en la expansión de:

(yo) (x – 1/x) ¹⁰

Solución:

Tenemos,

(x – 1/x) ¹⁰ donde, n = 10 (número par)

Entonces el término medio es (n/2 + 1) = (10/2 + 1) = (5 + 1) = 6 ^° término

Ahora,

T ₆ = T ₅₊₁

= ¹⁰ C ₅ (x) ^10-5 (–1/x) ⁵

= $-\frac{10×9×8×7×6}{5×4×3×2×1}$

= −252

(ii) (1 – 2x + x ² ) ^norte

Solución:

Tenemos, (1 – 2x + x ² ) ⁿ

= (1 – x) ²ⁿ

Aquí, n es un número par.

2n/2 + 1 = (n + 1) ^ésimo término

Ahora,

T _norte+1 = ²ⁿ C _norte (-1) ^norte x ^norte

= $\frac{(2n)!}{(n! )^2}( - 1 )^n x^n$

^{(iii) ( 1} + 3x + 3×2 + ^x3 ) ²ⁿ

Solución:

Tenemos, (1 + 3x + 3 x ² + x ³ ) ²ⁿ

= (1 + x) ⁶ⁿ

Aquí, n es un número par.

(6n/2 + 1) = (3n + 1) ^ésimo término

Ahora,

T _3n+1 = ⁶ⁿ C _3n x ³ⁿ

= $\frac{(6n)!}{(3n! )^2} x^{3n}$

(iv) (2x – x ² /4) ⁹

Solución:

Tenemos,

(2x – x ² /4) ⁹ donde, n = 9 (número impar)

Entonces los términos medios son ((n + 1)/2) = ((9 + 1)/2) = 10/2 = 5 y

((n + 1)/2 + 1) = ((9 + 1)/2 + 1) = (10/2 + 1) = (5 + 1) = 6

Los términos son ^5º y ^6º .

Ahora,

T ₅ = T ₄₊₁

= ⁹ C ₄ (2x) ^9-4 (–x ² /4) ⁴

= $\frac{9×8×7×6}{4×3×2×1}×\frac{2^5}{4^4}×x^{5+8}$

= $\frac{63}{4}x^{13}$

Y, T ₆ = T ₅₊₁

= ⁹ C ₅ (2x) ^9-5 (–x ² /4) ⁵

= $-\frac{9×8×7×6}{4×3×2×1}×\frac{2^4}{4^5}×x^{4+10}$

= $-\frac{63}{32}x^{14}$

(v) (x – 1/x) ²ⁿ⁺¹

Solución:

Tenemos, (x – 1/x) ²ⁿ⁺¹

Aquí, 2n + 1 es un número impar.

((2n + 1 + 1)/2) y (( ²ⁿ + 1 + 1)/2 + 1) ^términos .

Los términos son (n + 1) ^th y (n + 2) ^th

Ahora

Tn ₊₁ = $^{2n + 1}{}{C}_n x^{2n + 1 - n} \times \frac{( - 1 )^n}{x^n}$

=(-1) ^norte ²ⁿ⁺¹ C _norte x

Y Tn ₊₂ = Tn ₊₁₊₁

= $^{2n + 1}{}{C}_{n + 1} x^{2n + 1 - n - 1} \frac{( - 1 )^{n + 1}}{x^{n + 1}}$

= $(- 1)^{n + 1} \\^{2n + 1}C_{n + 1} \times \frac{1}{x}$

(vi) (x/3 + 9y) ¹⁰

Solución:

Tenemos,

(x/3 + 9y) ¹⁰ donde, n = 10 (número par)

Entonces el término medio es (n/2 + 1) = (10/2 + 1) = (5 + 1) = 6 ^° término.

Ahora,

T ₆ = T ₅₊₁

= ¹⁰ C ₅ (x/3) ^10-5 (9y) ⁵

= $\frac{109876}{54323^5}9^5x^5y^5$

= 61236 x ⁵ y ⁵

(vii) (3 – x ³ /6) ⁷

Solución:

Tenemos,

(3 – x ³ /6) ⁷ donde, n = 7 (número impar).

Entonces los términos medios son ((n + 1)/2) = ((7 + 1)/2) = 8/2 = 4 y

((n + 1)/2 + 1) = ((7 + 1)/2 + 1) = (8/2 + 1) = (4 + 1) = 5

Los términos son ^4º y ^5º .

Ahora,

T4 = T3 ₊₁

= ⁷ C ₃ (3) ^7-3 (-x ³ /6) ³

= $-\frac{765}{321}3^4\frac{x^9}{216}$

= $-\frac{105}{8}x^9$

Y, T ₅ = T ₄₊₁

= ⁹ C ₄ (3) ^9-4 (-x ³ /6) ⁴

= $\frac{765}{321}3^5\frac{x^{12}}{6^4}$

= $\frac{35}{48}x^{12}$

(viii) (2ax – b/x ² ) ¹²

Solución:

Tenemos,

(2ax – b/x ² ) ¹² donde, n = 12 (número par).

Entonces los términos medios son (n/2 + 1) = (12/2 + 1) = ^7mo término

Ahora,

T ₇ = T ₆₊₁

= ¹² C ₆ (2ax) ^12-6 (-b/x ² ) ⁶

= ¹² C ₆ (2ax) ⁶ (b/x ² ) ⁶

= ¹² C ₆ (2 ⁶ a ⁶ x ⁶ )(b ⁶ /x ¹² )

= ¹² C ₆ (2 ⁶ a ⁶ b ⁶ /x ⁶ )

(ix) (p/x + x/p) ⁹

Solución:

Tenemos,

(p/x + x/p) ⁹ donde, n = 9 (número impar).

Entonces los términos medios son ((n + 1)/2) = ((9 + 1)/2) = 10/2 = 5 y

((n + 1)/2 + 1) = ((9 + 1)/2 + 1) = (10/2 + 1) = (5 + 1) = 6

Los términos son ^5º y ^6º .

Ahora,

T ₅ = T ₄₊₁

= ⁹ C ₄ (p/x) ^9-4 (x ³ /p) ⁴

= ⁹ C ₄ (p/x) ⁵ (x/p) ⁴

= ⁹ C ₄ (p/x)

Y, T ₆ = T ₅₊₁

= ⁹ C ₅ (p/x) ^9-5 (x/p) ⁵

= ⁹ C ₅ (p/x) ⁴ (x/p) ⁵

= ⁹ C ₅ (x/p)

(x) (x/a – a/x) ¹⁰

Solución:

Tenemos,

(x/a – a/x) ¹⁰ donde, n = 10 (número par).

Entonces los términos medios son (n/2 + 1) = (10/2 + 1) 6 ^° término

Ahora,

T ₆ = T ₅₊₁

= ¹⁰ C ₅ (x/a) ^10-5 (-a/x) ⁵

= – ¹⁰ C ₅ (x/a) ⁵ (a/x) ⁵

= – ¹⁰ C ₅

= -252

Pregunta 16. Encuentra el término independiente de x en la expansión de las siguientes expresiones:

(yo) (3/2 x ² – 1/3x) ⁹

Solución:

Tenemos,

(3 /2×2 – ¹ /3x) ⁹

Sabemos que el (r+1) ^ésimo término de la expresión viene dado por,

T _r+1 = ^norte C _r X ^n-r un ^r

= ⁹ C _r (3/2x ² ) ^9-r (-1/3x) ^r

= $(-1)^r (^9C_r) (\frac{3^{9-2r}}{2^{9-r}}) x^{18-2r-r}$

Para que este término sea independiente de x, debemos tener

=> 18 – 3r = 0

=> 3r = 18

=> r = 18/3

=> r = 6

Entonces, el término requerido es el ^7mo término.

Entonces, T ₇ = T ₆₊₁

= ⁹ C ₆ × (3 ^9-12 )/(2 ^9-6 )

= $\frac{9×8×7}{3×2}× 3^{-3} × 2^{-3}$

= 7/18

Por tanto, el término independiente de x es 7/18.

(ii) (2x + 1/3x ² ) ⁹

Solución:

Tenemos,

(2x + 1/3x ² ) ⁹

Sabemos que el (r+1) ^ésimo término de la expresión viene dado por,

T _r+1 = ^norte C _r X ^n-r un ^r

= ⁹ C _r (2x) ^9-r (1/3x ² ) ^r

= $^9C_r(\frac{2^{9-r}}{3^r})x^{9-r-2r}$

Para que este término sea independiente de x, debemos tener

=> 9 – 3r = 0

=> r = 3

Entonces, el término requerido es el ^4to término.

Entonces, T ₇ = T ₆₊₁

= ⁹ C ₆ × (2 ^9-3 )/(3 ³ )

= $\frac{9×8×7}{3×2×1}×\frac{64}{27}$

= 5376/27

(iii) (2x ² – 3/x ³ ) ²⁵

Solución:

Tenemos,

(2x ² – 3/x ³ ) ²⁵

Sabemos que el (r+1) ^ésimo término de la expresión viene dado por,

T _r+1 = ^norte C _r X ^n-r un ^r

= ²⁵ C _r (2x ² ) ^25-r (-3/x ³ ) ^r

= (-1) ^r ²⁵ C _r × 2 ^25-r × 3 ^r x ^50-2r-3r

Para que este término sea independiente de x, debemos tener

=> 50 – 5r = 0

=> 5r = 50

=> r = 10

Entonces, el término requerido es el término ¹¹ .

Entonces, T ₁₁ = T ₁₀₊₁

= (-1) ¹⁰ ²⁵ C ₁₀ × 2 ^25-10 × 3 ¹⁰

= ²⁵ C ₁₀ (2 ¹⁵ × 3 ¹⁰ )

(iv) (3x – 2/x ² ) ¹⁵

Solución:

Tenemos,

(3x – 2/x ² ) ¹⁵

Sabemos que el (r+1) ^ésimo término de la expresión viene dado por,

T _r+1 = ^norte C _r X ^n-r un ^r

= ¹⁵ C _r (3x) ^15-r (-2/x ² ) ^r

= (-1) ^r ¹⁵ C _r × 3 ^15-r × 2 ^r x ^15-r-2r

Para que este término sea independiente de x, debemos tener

=> 15 – 3r = 0

=> 3r = 15

=> r = 5

Entonces, el término requerido es el sexto ^término .

Entonces, T ₆ = T ₅₊₁

= (-1) ⁵ ¹⁵ C5 × 3 ^15-5 × 25

= −3003 × 3 ¹⁰ × 25

(v) 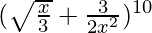$(\sqrt{\frac{x}{3}} + \frac{3}{2 x^2})^{10}$

Solución:

Tenemos

$(\sqrt{\frac{x}{3}} + \frac{3}{2 x^2})^{10}$

Sabemos que el (r+1) ^ésimo término de la expresión viene dado por,

Ahora,

Tr ₊₁ = $^{10}{}{C}_r \left( \sqrt{\frac{x}{3}} \right)^{10 - r} \left( \frac{3}{2 x^2} \right)^r$

= $^{10}{}{C}_r . \frac{3^{r - \frac{10 - r}{2}}}{2^r} x^\frac{10 - r}{2} - 2r$

Para que este término sea independiente de x, debemos tener

=> (10-r)/2 – 2r = 0

=> 10 – 5r = 0

=> r = 2

Por lo tanto, el término requerido es el 3 ^º término.

Entonces, T ₃ = T ₂₊₁

T ₃ = $^{10}{}{C}_2 \times \frac{3^{2 - \frac{10 - 2}{2}}}{2^2}$

= $\frac{10 \times 9}{2 \times 4 \times 9}$

= 5/4

(vi) $\left( x - \frac{1}{x^2} \right)^{3n}$

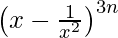
Solución:

Tenemos

$\left( x - \frac{1}{x^2} \right)^{3n}$

Sabemos que el (r+1) ^ésimo término de la expresión viene dado por,

Ahora,

Tr ₊₁ = $^{3n}{}{C}_r x^{3n - r} \left( \frac{- 1}{x^2} \right)^r$

= (-1) ^r ³ⁿ C _r x ^3n-r-2r a ^r

Para que este término sea independiente de x, debemos tener}

=> 3n – 3r = 0

=> r = norte

Entonces, el término requerido es (n + 1) el término ^th .

Asi que,

T _n+1 = (-1) ^{norte 3n} C _norte

(vii) 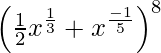$\left( \frac{1}{2} x^{\frac{1}{3}} + x^{\frac{- 1}{5}} \right)^8$

Solución:

Tenemos

$\left( \frac{1}{2} x^{\frac{1}{3}} + x^{\frac{- 1}{5}} \right)^8$

Sabemos que el (r+1) ^ésimo término de la expresión viene dado por,

Ahora,

Tr ₊₁ = $^{8}{}{C}_r \left( \frac{1}{2} x^{\frac{1}{3}} \right)^{8 - r} ( x^{\frac{- 1}{5}} )^r$

= $^{8}{}{C}_r . \frac{1}{2^{8 - r}} x^\frac{8 - r}{3} - \frac{r}{5}$

Para que este término sea independiente de x, debemos tener

=> (8 – r)/3 – r/5 = 0

=> 40 – 5r – 3r = 0

=> 8r = 40

=> r = 5

Entonces, el término requerido es el sexto ^término .

Entonces, T ₆ = T ₅₊₁

T ₆ = $^{8}{}{C}_5 \times \frac{1}{2^{8 - 5}}$

= $\frac{8 \times 7 \times 6}{3 \times 2 \times 8}$

= 7

(viii) (1 + x + 2x ³ ) (3/2x ² – 3/3x) ⁹

Solución:

Tenemos

(1 + x + 2x ³ ) (3/2x ² – 3/3x) ⁹

Sabemos que el (r+1) ^ésimo término de la expresión viene dado por,

Ahora,

V _r+1 = (1 + x + 2x ³ ) [(3/2x ² ) – ⁹ C ₁ (3/2x ² ) ⁸ (1/3x) + . . . – ⁹ C ₇ (3/2x ² ) ² (1/3x) ⁷ ]

Para que este término sea independiente de r, debemos tener

= ⁹ C ₆ (3 ³ /2 ³ ) (1/3 ⁶ ) – 2x ³ ⁹ C ₇ (2 ³ /3 ³ ) (1/3 ⁷ ) (1/x ³ )

= 18/7 – 27/2

= (189 – 36)/486

= 153/486

= 17/54

(ix) $\left( \sqrt[3]{x} + \frac{1}{2 \sqrt[3]{x}} \right)^{18}$ , x > 0

Solución:

Tenemos

$\left( \sqrt[3]{x} + \frac{1}{2 \sqrt[3]{x}} \right)^{18}$

Sabemos que el (r+1) ^ésimo término de la expresión viene dado por,

Ahora,

Tr ₊₁ = $^{18}{}{C}_r ( x^{1/3} )^{18 - r} \left( \frac{1}{2 x^{1/3}} \right)^r$

= $^{18}{}{C}_r \times \frac{1}{2^r} x^\frac{18 - r}{3} - \frac{r}{3}$

Para que este término sea independiente de r, debemos tener

=> (18 – r)/3 – r/3 = 0

=> 18 – 2r = 0

=> r = 9

Entonces, el término requerido es el ^noveno término.

Entonces, T ₉ = T ₈₊₁

T ₉ = ¹⁸ C ₉ (1/2 ⁹ )

(X) 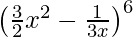$\left( \frac{3}{2} x^2 - \frac{1}{3x} \right)^6$

Solución:

Tenemos

$\left( \frac{3}{2} x^2 - \frac{1}{3x} \right)^6$

Supongamos que el (r + 1) ^enésimo término de la expresión dada es independiente de x.

Ahora,

Tr ₊₁ = $^{6}{}{C}_r \left( \frac{3}{2} x^2 \right)^{6 - r} \left( \frac{- 1}{3x} \right)^r$

= $\left( - 1 \right)^r\\^6C_r \times \frac{3^{6 - r - r}}{2^{6 - r}} x^{12 - 2r - r}$

Para que este término sea independiente de x, debemos tener

=> 12 – 3r = 0

=> r = 4

Por lo tanto, el término requerido es el cuarto ^término .

Entonces, T4 ₌ T3 ₊₁

= $^{6}{}{C}_4 \times \frac{3^{6 - 4 - 4}}{2^{6 - 4}}$

$= \frac{6 \times 5}{2 \times 1 \times 4 \times 9}$

= 5/12

Pregunta 17. Si los coeficientes de (2r + 4) ^th y (r – 2) ^th términos en la expansión de (1 + x) ¹⁸ son iguales, encuentre r.

Solución:

Se nos da,

(1 + x) ¹⁸

Sabemos que el coeficiente del término r ^-ésimo en la expansión de (1 + x) ⁿ es ⁿ C _r-1 .

Entonces, los coeficientes de (2r + 4) ^th y (r – 2) ^th términos en la expansión dada son,

¹⁸ C _2r+4-1 y ¹⁸ C _r-2-1

De acuerdo con la pregunta, tenemos,

=> ¹⁸ C _2r+4-1 = ¹⁸ C _r-2-1

=> ¹⁸ C _2r+3 = ¹⁸ C _r-3

Sabemos que si ⁿ C _r = ⁿ C _s , entonces r = s o r + s = n.

=> 2r + 3 = r – 3 o 2r + 3 + r – 3 = 18

=> 2r – r = –3 – 3 o 3r = 18 – 3 + 3

=> r = –6 o 3r = 18

=> r = –6 o r = 6

Ignorando r = – 6 ya que r no puede ser negativo.

Por lo tanto, el valor de r es 6.

Pregunta 18. Si los coeficientes de (2r + 1) ^th term y (r + 2) ^th term en la expansión de (1 + x) ⁴³ son iguales, encuentre r.

Solución:

Se nos da,

(1 + x) ⁴³

Sabemos que el coeficiente del término r ^-ésimo en la expansión de (1 + x) ⁿ es ⁿ C _r-1 .

Entonces, los coeficientes de (2r + 1) ^th y (r + 2) ^th términos en la expansión dada son,

⁴³ C _2r+1-1 y ⁴³ C _r+2-1

De acuerdo con la pregunta, tenemos,

=> ⁴³ C _2r+1-1 = ⁴³ C _r+2-1

=> ⁴³ C _2r = ⁴³ C _r+1

Sabemos que si ⁿ C _r = ⁿ C _s , entonces r = s o r + s = n.

=> 2r = r + 1 o 2r + r + 1 = 43

=> r = 1 o 3r = 42

=> r = 1 o r = 14

Ignorando r = 1 ya que da el mismo término en ambos lados.

Por lo tanto, el valor de r es 14.

Pregunta 19. Demostrar que el coeficiente de (r + 1) ^th término en la expansión de (1 + x) ⁿ⁺¹ es igual a la suma de los coeficientes de r ^th y (r+1) ^th términos en la expansión de (1 + x) ^norte .

Solución:

Sabemos que los coeficientes de (r + 1) el ^término en (1 + x) ⁿ⁺¹ es ⁿ⁺¹ C _r .

Entonces, la suma de los coeficientes de los términos r ^th y (r + 1) ^th en (1 + x) ⁿ es,

(1 + x) norte = ^norte C ^r_-1 + _norte C ^r

Como, ⁿ C _r+1 + ⁿ C _r = ⁿ⁺¹ C _r+1

= ⁿ⁺¹ C _r

Por lo tanto probado.

Pregunta 20. Demuestra que el término independiente de x en el desarrollo de (x + 1/x) ²ⁿ es 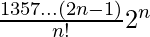$\frac{1×3×5×7...(2n-1)}{n!}×2^n$ .

Solución:

Tenemos,

(x + 1/x) ²ⁿ

Sabemos que el (r + 1) ^ésimo término está dado por,

T _r+1 = ^norte C _r X ^n-r un ^r

= ²ⁿ C _r x ^2n-r (1/x) ^r

= ²ⁿ C _r x ^2n-2r

Para que este término sea independiente de x, debemos tener,

=> 2n − 2r = 0

=> 2n = 2r

=> r = norte

Por lo tanto, el término requerido es (n+1) el ^término .

T _n+1 = ²ⁿ C norte x ^2n-n₍ 1/x) ^norte

= ²ⁿ C _norte

= $\frac{2n!}{n!n!}$

= $\frac{2n(2n-1)(2n-2)...5×4×3×2×1}{n!n!}$

= $\frac{(1×3×5×...(2n-1))×2^n(1×2×3×4...n)}{n!n!}$

= $\frac{(1×3×5×...(2n-1))×2^n×n!}{n!n!}$

= $\frac{1×3×5×7...(2n-1)}{n!}×2^n$

Por lo tanto probado.

Pregunta 21. Si los coeficientes de los términos 5º ^{, 6º} y ^7º de ^la expansión (1 + x) ⁿ están en AP, encuentre n.

Solución:

Tenemos, (1 + x) ⁿ

Sabemos que el coeficiente del r ^-ésimo término de una expresión binomial está dado por ⁿ C _r-1 .

Coeficiente del 5 ^° término = ⁿ C _5-1 = ⁿ C ₄

Coeficiente del sexto ^término = ⁿ C _6-1 = ⁿ C ₅

Coeficiente del ^7mo término = ⁿ C _7-1 = ⁿ C ₆

De acuerdo con la pregunta, tenemos,

=> 2 ^norte C ₅ = ^norte C ₄ + ^norte C ₆

=> $2[\frac{n!}{(n-5)!5!}] = \frac{n!}{(n-4)!4!} + \frac{n!}{(n-6)!6!}$

=> $\frac{2}{(n-5)!5!}=\frac{1}{(n-4)!4!} + \frac{1}{(n-6)!6!}$

=> $\frac{2}{(n-5)(n-6)!×5×4!}=\frac{1}{(n-4)(n-5)(n-6)!×4!} + \frac{1}{(n-6)!×6×5×4!}$

=> $\frac{2}{(n-5)×5}=\frac{1}{(n-4)(n-5)} + \frac{1}{6×5}$

=> $\frac{2}{5}=\frac{1}{n-4} + \frac{n-5}{30}$

=> $\frac{2}{5}=\frac{30+n^2-9n+20}{30(n-4)}$

=> 60(n−4) = 150 + 5n ² − 45n + 100

=> 60n − 240 = 250 + 5n ² − 45n

=> 5n ² − 105n + 490 = 0

=> norte ² − 21n + 98 = 0

=> norte ² − 7n − 14n + 98 = 0

=> norte (norte – 7) – 14 (norte – 7) = 0

=> (n − 7) (n − 14) = 0

=> n = 7 o n = 14

Por lo tanto, el valor de n es 7 o 14.

Pregunta 22. Si los coeficientes de los términos 2, 3 y 4 de la expansión (1 + x) ²ⁿ están en AP, demuestre que 2n ² − 9n + 7 = 0.

Solución:

Tenemos, (1 + x) ²ⁿ

Sabemos que el coeficiente del r ^-ésimo término de una expresión binomial está dado por ⁿ C _r-1 .

Coeficiente del ^2do término = ²ⁿ C _2-1 = ²ⁿ C ₁

Coeficiente del 3er ^término = ²ⁿ C _3-1 = ²ⁿ C ₂

Coeficiente del 4 ^° término = ²ⁿ C _4-1 = ²ⁿ C ₃

De acuerdo con la pregunta, tenemos,

=> 2 ²ⁿ C ₂ = ²ⁿ C ₁ + ²ⁿ C ₃

=> 2 = $\frac{^{2n}C_1}{^{2n}C_2}+\frac{^{2n}C_3}{^{2n}C_2}$

=> 2 = $\frac{2}{2n-2+1}+\frac{2n-3+1}{3}$

=> $\frac{2}{2n-1}+\frac{2n-2}{3}$ = 2

=> $\frac{6+4n^2-4n-2n+2}{3(2n-1)}$ = 2

=> 4n ² − 6n + 8 = 12n − 6

=> 4n ² − 18n + 14 = 0

=> 2 (2n ² − 9n + 7) = 0

=> 2n ² − 9n + 7 = 0

Por lo tanto probado.

Pregunta 23. En la expansión de (1 + x) ⁿ , los coeficientes binomiales de tres términos consecutivos son respectivamente 220, 495 y 792, encuentre el valor de n.

Solución:

Tenemos, (1 + x) ⁿ

Sean los tres términos consecutivos r ^th , (r+1) ^th y (r+2) ^th .

Sabemos que el coeficiente del r ^-ésimo término de una expresión binomial está dado por ⁿ C _r-1 .

Coeficiente del término r ^th = ⁿ C _r-1 = 220

Coeficiente de (r+1) ^th término = ⁿ C _r+1-1 = ⁿ C _r = 495

Coeficiente de (r+2) ^th término = ⁿ C _r+2-1 = ⁿ C _r+1 = 792

Ahora, $\frac{^nC_{r+1}}{^nC_r}=\frac{792}{495}$

=> $\frac{n-(r+1)+1}{r+1}=\frac{792}{495}$

=> $\frac{n-r}{r+1}=\frac{8}{5}$

=> 5n − 5r = 8r + 8

=> 5n – 13r = 8 . . . . (1)

También, $\frac{^nC_{r}}{^nC_{r-1}}=\frac{495}{220}$

=> $\frac{n-r+1}{r}=\frac{9}{4}$

=> 4n − 4r + 4 = 9r

=> 4n − 13r = −4 . . . . (2)

Restando (2) de (1), obtenemos,

=> norte = 8 + 4

=> norte = 12

Por lo tanto, el valor de n es 12.

Pregunta 24. Si los coeficientes de los términos 2 ^, 3 y 4 ^de la expansión (1 + x) ⁿ^están en AP, entonces encuentre el valor de n.

Solución:

Tenemos, (1 + x) ⁿ

Sabemos que el coeficiente del r ^-ésimo término de una expresión binomial está dado por ⁿ C _r-1 .

Coeficiente del segundo _término = ⁿ C _2-1 = ⁿ C ¹

Coeficiente del 3er ^término = ⁿ C _3-1 = ⁿ C ₂

Coeficiente del 4 ^° término = ⁿ C _4-1 = ⁿ C ₃

De acuerdo con la pregunta, tenemos,

=> 2 ^norte C ₂ = ^norte C ₁ + ^norte C ₃

=> $2 = \frac{^{n}C_1}{^{n}C_2}+\frac{^{n}C_3}{^{n}C_2}$

=> $2 = \frac{2}{n-2+1}+\frac{n-3+1}{3}$

=> $\frac{2}{n-1}+\frac{n-2}{3} = 2$

=> $\frac{6+n^2-3n+2}{3(n-1)}$ = 2

=> norte ² − 3n + 8 = 6 (norte − 1)

=> norte ² − 3n + 8 = 6n − 6

=> norte ² − 9n + 14 = 0

=> norte ² − 7n − 2n + 14 = 0

=> norte (n−7) − 2 (n−7) = 0

=> (norte – 2) (norte – 7) = 0

=> n = 2 o n = 7

Ignorando n = 2 ya que no satisface nuestra condición.

Por lo tanto, el valor de n es 7.

Pregunta 25. Si en el desarrollo de (1 + x) ⁿ , los coeficientes de p ^th yq ^th términos son iguales, entonces demuestre que p + q = n + 2, donde p ≠ q.

Solución:

Tenemos, (1 + x) ⁿ

Sabemos que el coeficiente del r ^-ésimo término de una expresión binomial está dado por ⁿ C _r-1 .

Coeficiente de p ^ésimo término = ⁿ C _p-1

Coeficiente de q ^th término = ⁿ C _q-1

De acuerdo con la pregunta, tenemos,

=> ⁿ C _p-1 = ⁿ C _q-1

=> pags − 1 = q − 1 o pags − 1 + q − 1 = norte

=> pags = q o pags + q − 2 = norte

=> pags + q − 2 = norte

=> pags + q = norte + 2

Por lo tanto probado.

Pregunta 26. Si en la expansión de (1 + x) ⁿ , los coeficientes binomiales de tres términos consecutivos son respectivamente 56, 70 y 56, encuentre n y la posición de los términos de estos coeficientes.

Solución:

Tenemos, (1 + x) ⁿ

Sean los tres términos consecutivos r ^th , (r+1) ^th y (r+2) ^th .

Sabemos que el coeficiente del r ^-ésimo término de una expresión binomial está dado por ⁿ C _r-1 .

Coeficiente del término r ^th = ⁿ C _r-1 = 56

Coeficiente de (r+1) ^th término = ⁿ C _r+1-1 = ⁿ C _r = 70

Coeficiente de (r+2) ^th término = ⁿ C _r+2-1 = ⁿ C _r+1 = 56

Ahora, $\frac{^nC_{r+1}}{^nC_r}=\frac{56}{70}$

=> $\frac{n-(r+1)+1}{r+1}=\frac{56}{70}$

=> $\frac{n-r}{r+1}=\frac{4}{5}$

=> 5n − 5r = 4r + 4

=> 5n – 9r = 4 . . . . (1)

También, $\frac{^nC_{r}}{^nC_{r-1}}=\frac{70}{56}$

=> $\frac{n-r+1}{r}=\frac{5}{4}$

=> 4n − 4r + 4 = 5r

=> 4n – r = -4 . . . . (2)

Restando (2) de (1), obtenemos,

=> norte = 4 + 4

=> norte = 8

Poniendo n = 8 en (1), obtenemos,

=> 5(8) − 9r = 4

=> 40 − 9r = 4

=> 9r = 36

=> r = 4

Por lo tanto, tres términos consecutivos son los términos ^4º^, 5º y ^6º .

Publicación traducida automáticamente

Artículo escrito por gurjotloveparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 11 Soluciones RD Sharma – Capítulo 18 Teorema del binomio – Ejercicio 18.2 | conjunto 2

Pregunta 14. Encuentra los términos medios en la expansión de:

(yo) (3x – x ^3/6 ) ⁹

(ii) (2x ² – 1/x) ⁷

(iii) (3x – 2/x ² ) ¹⁵

(iv) (x ⁴ – 1/x ³ ) ¹¹

Pregunta 15. Encuentra los términos medios en la expansión de:

(yo) (x – 1/x) ¹⁰

(ii) (1 – 2x + x ² ) ^norte

^{(iii) ( 1} + 3x + 3×2 + ^x3 ) ²ⁿ

(iv) (2x – x ² /4) ⁹

(v) (x – 1/x) ²ⁿ⁺¹

(vi) (x/3 + 9y) ¹⁰

(vii) (3 – x ³ /6) ⁷

(viii) (2ax – b/x ² ) ¹²

(ix) (p/x + x/p) ⁹

(x) (x/a – a/x) ¹⁰

Pregunta 16. Encuentra el término independiente de x en la expansión de las siguientes expresiones:

(yo) (3/2 x ² – 1/3x) ⁹

(ii) (2x + 1/3x ² ) ⁹

(iii) (2x ² – 3/x ³ ) ²⁵

(iv) (3x – 2/x ² ) ¹⁵

(v) $(\sqrt{\frac{x}{3}} + \frac{3}{2 x^2})^{10}$

(vi) $\left( x - \frac{1}{x^2} \right)^{3n}$

(vii) $\left( \frac{1}{2} x^{\frac{1}{3}} + x^{\frac{- 1}{5}} \right)^8$

(viii) (1 + x + 2x ³ ) (3/2x ² – 3/3x) ⁹

(ix) $\left( \sqrt[3]{x} + \frac{1}{2 \sqrt[3]{x}} \right)^{18}$ , x > 0

(X) $\left( \frac{3}{2} x^2 - \frac{1}{3x} \right)^6$

Pregunta 17. Si los coeficientes de (2r + 4) ^th y (r – 2) ^th términos en la expansión de (1 + x) ¹⁸ son iguales, encuentre r.

Pregunta 18. Si los coeficientes de (2r + 1) ^th term y (r + 2) ^th term en la expansión de (1 + x) ⁴³ son iguales, encuentre r.

Pregunta 19. Demostrar que el coeficiente de (r + 1) ^th término en la expansión de (1 + x) ⁿ⁺¹ es igual a la suma de los coeficientes de r ^th y (r+1) ^th términos en la expansión de (1 + x) ^norte .

Pregunta 20. Demuestra que el término independiente de x en el desarrollo de (x + 1/x) ²ⁿ es $\frac{1×3×5×7...(2n-1)}{n!}×2^n$ .

Pregunta 21. Si los coeficientes de los términos 5º ^{, 6º} y ^7º de ^la expansión (1 + x) ⁿ están en AP, encuentre n.

Pregunta 22. Si los coeficientes de los términos 2, 3 y 4 de la expansión (1 + x) ²ⁿ están en AP, demuestre que 2n ² − 9n + 7 = 0.

Pregunta 23. En la expansión de (1 + x) ⁿ , los coeficientes binomiales de tres términos consecutivos son respectivamente 220, 495 y 792, encuentre el valor de n.

Pregunta 24. Si los coeficientes de los términos 2 ^, 3 y 4 ^de la expansión (1 + x) ⁿ^están en AP, entonces encuentre el valor de n.

Pregunta 25. Si en el desarrollo de (1 + x) ⁿ , los coeficientes de p ^th yq ^th términos son iguales, entonces demuestre que p + q = n + 2, donde p ≠ q.

Pregunta 26. Si en la expansión de (1 + x) ⁿ , los coeficientes binomiales de tres términos consecutivos son respectivamente 56, 70 y 56, encuentre n y la posición de los términos de estos coeficientes.

Deja una respuesta Cancelar la respuesta

Pregunta 14. Encuentra los términos medios en la expansión de:

(yo) (3x – x 3/6 ) 9

(ii) (2x 2 – 1/x) 7

(iii) (3x – 2/x 2 ) 15

(iv) (x 4 – 1/x 3 ) 11

Pregunta 15. Encuentra los términos medios en la expansión de:

(yo) (x – 1/x) 10

(ii) (1 – 2x + x 2 ) norte

(iii) ( 1 + 3x + 3×2 + x3 ) 2n

(iv) (2x – x 2 /4) 9

(v) (x – 1/x) 2n+1

(vi) (x/3 + 9y) 10

(vii) (3 – x 3 /6) 7

(viii) (2ax – b/x 2 ) 12

(ix) (p/x + x/p) 9

(x) (x/a – a/x) 10

Pregunta 16. Encuentra el término independiente de x en la expansión de las siguientes expresiones:

(yo) (3/2 x 2 – 1/3x) 9

(ii) (2x + 1/3x 2 ) 9

(iii) (2x 2 – 3/x 3 ) 25

(iv) (3x – 2/x 2 ) 15

(v)

(vi)

(vii)

(viii) (1 + x + 2x 3 ) (3/2x 2 – 3/3x) 9

(ix) , x > 0

(X)

Pregunta 17. Si los coeficientes de (2r + 4) th y (r – 2) th términos en la expansión de (1 + x) 18 son iguales, encuentre r.

Pregunta 18. Si los coeficientes de (2r + 1) th term y (r + 2) th term en la expansión de (1 + x) 43 son iguales, encuentre r.

Pregunta 19. Demostrar que el coeficiente de (r + 1) th término en la expansión de (1 + x) n+1 es igual a la suma de los coeficientes de r th y (r+1) th términos en la expansión de (1 + x) norte .

Pregunta 20. Demuestra que el término independiente de x en el desarrollo de (x + 1/x) 2n es .

Pregunta 21. Si los coeficientes de los términos 5º , 6º y 7º de la expansión (1 + x) n están en AP, encuentre n.

Pregunta 22. Si los coeficientes de los términos 2, 3 y 4 de la expansión (1 + x) 2n están en AP, demuestre que 2n 2 − 9n + 7 = 0.

Pregunta 23. En la expansión de (1 + x) n , los coeficientes binomiales de tres términos consecutivos son respectivamente 220, 495 y 792, encuentre el valor de n.

Pregunta 24. Si los coeficientes de los términos 2 , 3 y 4 de la expansión (1 + x) n están en AP, entonces encuentre el valor de n.

Pregunta 25. Si en el desarrollo de (1 + x) n , los coeficientes de p th yq th términos son iguales, entonces demuestre que p + q = n + 2, donde p ≠ q.

Pregunta 26. Si en la expansión de (1 + x) n , los coeficientes binomiales de tres términos consecutivos son respectivamente 56, 70 y 56, encuentre n y la posición de los términos de estos coeficientes.

Deja una respuesta Cancelar la respuesta

(yo) (3x – x ^3/6 ) ⁹

(ii) (2x ² – 1/x) ⁷

(iii) (3x – 2/x ² ) ¹⁵

(iv) (x ⁴ – 1/x ³ ) ¹¹

(yo) (x – 1/x) ¹⁰

(ii) (1 – 2x + x ² ) ^norte

^{(iii) ( 1} + 3x + 3×2 + ^x3 ) ²ⁿ

(iv) (2x – x ² /4) ⁹

(v) (x – 1/x) ²ⁿ⁺¹

(vi) (x/3 + 9y) ¹⁰

(vii) (3 – x ³ /6) ⁷

(viii) (2ax – b/x ² ) ¹²

(ix) (p/x + x/p) ⁹

(x) (x/a – a/x) ¹⁰

(yo) (3/2 x ² – 1/3x) ⁹

(ii) (2x + 1/3x ² ) ⁹

(iii) (2x ² – 3/x ³ ) ²⁵

(iv) (3x – 2/x ² ) ¹⁵

(v) $(\sqrt{\frac{x}{3}} + \frac{3}{2 x^2})^{10}$

(vi) $\left( x - \frac{1}{x^2} \right)^{3n}$

(vii) $\left( \frac{1}{2} x^{\frac{1}{3}} + x^{\frac{- 1}{5}} \right)^8$

(viii) (1 + x + 2x ³ ) (3/2x ² – 3/3x) ⁹

(ix) $\left( \sqrt[3]{x} + \frac{1}{2 \sqrt[3]{x}} \right)^{18}$ , x > 0

(X) $\left( \frac{3}{2} x^2 - \frac{1}{3x} \right)^6$

Pregunta 17. Si los coeficientes de (2r + 4) ^th y (r – 2) ^th términos en la expansión de (1 + x) ¹⁸ son iguales, encuentre r.

Pregunta 18. Si los coeficientes de (2r + 1) ^th term y (r + 2) ^th term en la expansión de (1 + x) ⁴³ son iguales, encuentre r.

Pregunta 19. Demostrar que el coeficiente de (r + 1) ^th término en la expansión de (1 + x) ⁿ⁺¹ es igual a la suma de los coeficientes de r ^th y (r+1) ^th términos en la expansión de (1 + x) ^norte .

Pregunta 20. Demuestra que el término independiente de x en el desarrollo de (x + 1/x) ²ⁿ es $\frac{1×3×5×7...(2n-1)}{n!}×2^n$ .

Pregunta 21. Si los coeficientes de los términos 5º ^{, 6º} y ^7º de ^la expansión (1 + x) ⁿ están en AP, encuentre n.

Pregunta 22. Si los coeficientes de los términos 2, 3 y 4 de la expansión (1 + x) ²ⁿ están en AP, demuestre que 2n ² − 9n + 7 = 0.

Pregunta 23. En la expansión de (1 + x) ⁿ , los coeficientes binomiales de tres términos consecutivos son respectivamente 220, 495 y 792, encuentre el valor de n.

Pregunta 24. Si los coeficientes de los términos 2 ^, 3 y 4 ^de la expansión (1 + x) ⁿ^están en AP, entonces encuentre el valor de n.

Pregunta 25. Si en el desarrollo de (1 + x) ⁿ , los coeficientes de p ^th yq ^th términos son iguales, entonces demuestre que p + q = n + 2, donde p ≠ q.

Pregunta 26. Si en la expansión de (1 + x) ⁿ , los coeficientes binomiales de tres términos consecutivos son respectivamente 56, 70 y 56, encuentre n y la posición de los términos de estos coeficientes.