Clase 11 Soluciones RD Sharma – Capítulo 18 Teorema del binomio – Ejercicio 18.2

Pregunta 27. Si los términos 3 ^,⁴ , 5 ^y 6 ^en el desarrollo de (x + α) ⁿ son respectivamente a, b, c y d, demuestre que 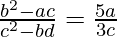$\frac{b^2-ac}{c^2-bd}=\frac{5a}{3c}$ .

Solución:

Nos dan, (x + α) ⁿ

Entonces, T ₃ = a = ⁿ C ₂ x ^n-2 α ²

T ₄ = segundo = norte C ₃ x ⁿ^-3 α ³

T ₅ = C = norte C ₄ x ⁿ^-4 α ⁴

T ₆ = re = norte C ₅ x ⁿ^-5 α ⁵

Tenemos que demostrar que, $\frac{b^2-ac}{c^2-bd}=\frac{5a}{3c}$

=> $\frac{b^2-ac}{a}=\frac{5(c^2-bd)}{3c}$

=> $\frac{b^2-ac}{ab}=\frac{5(c^2-bd)}{3bc}$

=> $\frac{b}{a}-\frac{c}{b}=\frac{5}{3}\left[\frac{c}{b}-\frac{d}{c}\right]$

=> $\frac{^nC_3x^{n-3}α^3}{^nC_2x^{n-2}α^2}-\frac{^nC_4x^{n-4}α^4}{^nC_3x^{n-3}α^3}=\frac{5}{3}\left[\frac{^nC_4x^{n-4}α^4}{^nC_3x^{n-3}α^3}-\frac{^nC_5x^{n-5}α^5}{^nC_4x^{n-4}α^4}\right]$

=> $\left[\frac{^nC_3}{^nC_2}-\frac{^nC_4}{^nC_3}\right]\frac{\alpha}{x}=\frac{5\alpha}{3x}\left[\frac{^nC_4}{^nC_3}-\frac{^nC_5}{^nC_4}\right]$

=> $\left[\frac{n-2}{3}-\frac{n-3}{4}\right]=\frac{5}{3}\left[\frac{n-3}{4}-\frac{n-4}{5}\right]$

=> $\frac{4n-8-3n+9}{12}=\frac{5}{3}\left[\frac{5n-15-4n+16}{20}\right]$

=> $\frac{n+1}{12}=\frac{5}{3}\left[\frac{n+1}{20}\right]$

=> $\frac{n+1}{12}=\frac{n+1}{12}$

Por lo tanto probado.

Pregunta 28. Si los términos 6 ^,⁷ , 8 ^y 9 ^en el desarrollo de (x + α) ⁿ son respectivamente a, b, c y d, demuestre que 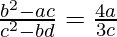$\frac{b^2-ac}{c^2-bd}=\frac{4a}{3c}$ .

Solución:

Nos dan, (x + α) ⁿ

Entonces, T ₆ = a = ⁿ C ₅ x ^n-5 α ⁵

T ₇ = segundo = norte C ₆ x ⁿ^-6 α ⁶

T ₈ = C = norte C ₇ x ⁿ^-7 α ⁷

T ₉ = re = norte C ₈ x ⁿ^-8 α ⁸

Tenemos que demostrar que, $\frac{b^2-ac}{c^2-bd}=\frac{4a}{3c}$

=> $\frac{b^2-ac}{a}=\frac{4(c^2-bd)}{3c}$

=> $\frac{b^2-ac}{ab}=\frac{4(c^2-bd)}{3bc}$

=> $\frac{b}{a}-\frac{c}{b}=\frac{4}{3}\left[\frac{c}{b}-\frac{d}{c}\right]$

=> $\frac{^nC_6x^{n-6}α^6}{^nC_5x^{n-5}α^5}-\frac{^nC_7x^{n-7}α^7}{^nC_6x^{n-6}α^6}=\frac{4}{3}\left[\frac{^nC_7x^{n-7}α^7}{^nC_6x^{n-6}α^6}-\frac{^nC_8x^{n-8}α^8}{^nC_7x^{n-7}α^7}\right]$

=> $\left[\frac{^nC_6}{^nC_5}-\frac{^nC_7}{^nC_6}\right]\frac{\alpha}{x}=\frac{4\alpha}{3x}\left[\frac{^nC_7}{^nC_6}-\frac{^nC_8}{^nC_7}\right]$

=> $\left[\frac{n-5}{6}-\frac{n-6}{7}\right]=\frac{4}{3}\left[\frac{n-6}{7}-\frac{n-7}{8}\right]$

=> $\frac{7n-35-6n+36}{42}=\frac{4}{3}\left[\frac{8n-48-7n+49}{56}\right]$

=> $\frac{n+1}{42}=\frac{4}{3}\left[\frac{n+1}{56}\right]$

=> $\frac{n+1}{42}=\frac{n+1}{42}$

Por lo tanto probado.

Pregunta 29. Si los coeficientes de tres términos consecutivos en la expansión de (1+x) ⁿ son respectivamente 76 , 95 y 76, encuentre n.

Solución:

Nos dan, (1+x) ⁿ

Sean los tres términos consecutivos r ^th , (r+1) ^th y (r+2) ^th .

Sabemos que el coeficiente del r ^-ésimo término de una expresión binomial está dado por ⁿ C _r-1 .

Coeficiente del término r ^th = ⁿ C _r-1 = 76

Coeficiente de (r+1) ^th término = ⁿ C _r+1-1 = ⁿ C _r = 95

Coeficiente de (r+2) ^th término = ⁿ C _r+2-1 = ⁿ C _r+1 = 76

Ahora, $\frac{^nC_{r+1}}{^nC_r}=\frac{76}{95}$

=> $\frac{n-(r+1)+1}{r+1}=\frac{76}{95}$

=> $\frac{n-r}{r+1}=\frac{4}{5}$

=> 5n − 5r = 4r + 4

=> 5n – 9r = 4 . . . . (1)

También, $\frac{^nC_{r}}{^nC_{r-1}}=\frac{95}{76}$

=> $\frac{n-r+1}{r}=\frac{5}{4}$

=> 4n − 4r + 4 = 5r

=> 4n – r = -4 . . . . (2)

Restando (2) de (1), obtenemos,

=> norte = 4 + 4

=> norte = 8

Por lo tanto, el valor de n es 8.

Pregunta 30. Si el 6 ^,⁷ y 8 en la ^expansión de (x + a) ⁿ son respectivamente 112, 7 y 1/4, encuentre x, a y n.

Solución:

Nos dan, (x + a) ⁿ

Además, T ₆ = ⁿ C ₅ x ^n-5 a ⁵ = 112

T ₇ = norte C ₆ x ⁿ^-6 un ⁶ = 7

T ₈ = norte C ₇ x ⁿ^-7 un ⁷ = 1/4

Ahora, $\frac{^nC_6x^{n-6}a^6}{^nC_5x^{n-5}a^5}=\frac{7}{112}$

=> $\frac{^nC_{n-6}x^{n-6}a^6}{^nC_{n-5}x^{n-5}a^5}=\frac{7}{112}$

=> $\frac{^nC_{n-6}}{^nC_{n-5}}×\frac{a}{x}=\frac{1}{16}$

=> $\frac{n-6+1}{n-(n-5)+1}×\frac{a}{x}=\frac{1}{16}$

=> $\frac{n-5}{6}×\frac{a}{x}=\frac{1}{16}$

=> $\frac{a}{x}=\frac{3}{8(n-5)}$ . . . . (1)

También, $\frac{^nC_7x^{n-7}a^7}{^nC_6x^{n-6}a^6}=\frac{\frac{1}{4}}{7}$

=> $\frac{^nC_{n-7}x^{n-7}a^7}{^nC_{n-6}x^{n-6}a^6}=\frac{1}{28}$

=> $\frac{^nC_{n-7}}{^nC_{n-6}}×\frac{a}{x}=\frac{1}{28}$

=> $\frac{n-7+1}{n-(n-6)+1}×\frac{a}{x}=\frac{1}{28}$

=> $\frac{n-6}{7}×\frac{a}{x}=\frac{1}{28}$

=> $\frac{a}{x}=\frac{1}{4(n-6)}$ . . . . (2)

De (1) y (2), obtenemos,

=> $\frac{3}{8(n-5)} = \frac{1}{4(n-6)}$

=> $\frac{3}{2(n-5)} = \frac{1}{n-6}$

=> 3n − 18 = 2n − 10

=> norte = 8

Poniendo n = 8 en (2), obtenemos,

=> $\frac{a}{x}=\frac{1}{4(8-6)}$

=> $\frac{a}{x}=\frac{1}{8}$

=> x = 8a

Ahora, ⁿ C ₅ x ^n-5 a ⁵ = 112

=> ⁸ C ₅ x ^8-5 a ⁵ = 112

=> ⁸ C ₅ (8a) ³ a ⁵ = 112

=> $\frac{8×7×6}{3×2}×512×a^3×a^5 = 112$

=> un ⁸ = $\frac{1}{256}$

=> un ⁸ = $(\frac{1}{2})^8$

=> un = 1/2

Entonces, x = 8 (1/2) = 4

Por tanto, el valor de x, a y n es 4, 1/2 y 8 respectivamente.

Pregunta 31. Si el ^2º , ^3º y 4º en la ^expansión de (x + a) ⁿ son respectivamente 240, 720 y 1080 respectivamente, encuentre x, a y n.

Solución:

Nos dan, (x + a) ⁿ

Además, T ₂ = ⁿ C ₁ x ^n-1 a = 240

T ₃ = norte C ₂ x ⁿ^-2 un ² = 720

T ₄ = norte C ₃ x ⁿ^-3 un ³ = 1080

Ahora, $\frac{^nC_3x^{n-3}a^3}{^nC_2x^{n-2}a^2}=\frac{1080}{720}$

=> $\frac{^nC_3}{^nC_2}×\frac{a}{x}=\frac{3}{2}$

=> $\frac{n-3+1}{2+1}×\frac{a}{x}=\frac{3}{2}$

=> $\frac{n-2}{3}×\frac{a}{x}=\frac{3}{2}$

=> $\frac{a}{x}=\frac{9}{2(n-2)}$ . . . . (1)

También, $\frac{^nC_2x^{n-2}a^2}{^nC_1x^{n-1}a}=\frac{720}{240}$

=> $\frac{^nC_2}{^nC_1}×\frac{a}{x}=3$

=> $\frac{n-2+1}{2}×\frac{a}{x}=3$

=> $\frac{n-1}{2}×\frac{a}{x}=3$

=> $\frac{a}{x}=\frac{6}{n-1}$ . . . . (2)

De (1) y (2), obtenemos,

=> $\frac{9}{2(n-2)}=\frac{6}{n-1}$

=> 12n − 24 = 9n − 9

=> 3n = 15

=> norte = 5

Poniendo n = 5 en (2), obtenemos,

=> $\frac{a}{x}=\frac{6}{5-1}$

=> $\frac{a}{x}=\frac{6}{4}$

=> $\frac{a}{x}=\frac{3}{2}$

=> $a = \frac{3}{2}x$

Ahora, ⁿ C ₁ x ^n-1 a = 240

=> ⁵ C ₁ x ^5-1 (3x/2) = 240

=> ⁵ C ₁ x ⁵ (3/2) = 240

=> $\frac{5×4!}{4!}×x^5×\frac{3}{2} = 240$

=> $x^5=\frac{240×2}{5×3}$

=> x ⁵ = 32

=> x ⁵ = 2 ⁵

=> x = 2

Entonces, a = (3/2) (2) = 3

Por lo tanto, el valor de x, a y n es 2, 3 y 5 respectivamente.

Pregunta 32. Encuentra a, b y n en la expansión de (a+b) ⁿ si los primeros tres términos son 729, 7290 y 30375 respectivamente.

Solución:

Nos dan, (a+b) ⁿ

Además, T ₁ = ⁿ C ₀ a ⁿ = 729

T ₂ = ^norte C ₁ un ^{norte-1 segundo}¹ = 7290

T ₃ = norte C ₂ un ⁿ^-2^{segundo 2} = 30375

Ahora, $\frac{^nC_1a^{n-1}b^1}{^nC_0a^n} = \frac{7290}{729}$

=> $^nC_{n-1}×\frac{b}{a} = 10$

=> $\frac{b}{a} = \frac{10}{n}$ . . . . (1)

También, $\frac{^nC_2a^{n-2}b^2}{^nC_1a^{n-1}b} = \frac{30375}{7290}$

=> $\frac{^nC_{n-2}}{^nC_{n-1}}×\frac{b}{a} = \frac{25}{6}$

=> $\frac{n-2+1}{n-(n-1)+1}×\frac{b}{a} = \frac{25}{6}$

=> $\frac{n-1}{2}×\frac{b}{a} = \frac{25}{6}$

=> $\frac{b}{a} = \frac{25}{3(n-1)}$ . . . . (2)

De (1) y (2), obtenemos,

=> $\frac{10}{n} = \frac{25}{3(n-1)}$

=> 30n − 30 = 25n

=> 5n = 30

=> norte = 6

Entonces, ⁿ C ₀ a ⁿ = 729

=> un ⁶ = 3 ⁶

=> un = 3

Poniendo a = 3 en (2), obtenemos,

=> $\frac{b}{3} = \frac{25}{3(6-1)}$

=> $\frac{b}{3} = \frac{5}{3}$

=> segundo = 5

Por lo tanto, el valor de a, b y n es 3, 5 y 6 respectivamente.

Pregunta 33. Encuentra a, si los coeficientes de x ² y x ³ en la expansión de (3+ax) ⁹ son iguales.

Solución:

Tenemos, (3+ax) ⁹ = ⁹ C ₀ 3 ⁹ + ⁹ C ₁ 3 ⁸ (ax) ¹ + ⁹ C ₂ 3 ⁷ (ax) ² + ⁹ C ₃ 3 ⁶ (ax) ³ + . . . .

Coeficiente de x ² = ⁹ C ₂ 3 ⁷ a ²

Coeficiente de x ³ = ⁹ C ₃ 3 ⁶ a ³

De acuerdo con la pregunta, tenemos,

=> ⁹ C ₂ 3 ⁷ un ² = ⁹ C ₃ 3 ⁶ un ³

=> $\frac{9×8}{2×1}×3=\frac{9×8×7}{3×2×1}×a$

=> 81 = 63a

=> un = 9/7

Por lo tanto, el valor de a es 9/7.

Pregunta 34. Encuentra a, si los coeficientes de x y x ³ en la expansión de (2+ax) ⁴ son iguales.

Solución:

Tenemos, (2+ax) ⁴ = ⁴ C ₀ 2 ⁴ + ⁴ C ₁ 2 ³ (ax) ¹ + ⁴ C ₂ 2 ² (ax) ² + ⁴ C ₃ 2 (ax) ³ + . . . .

Coeficiente de x = ⁴ C ₁ 2 ³ a

Coeficiente de x ³ = ⁴ C ₃ 2 a ³

De acuerdo con la pregunta, tenemos,

=> ⁴ C ₁ 2 ³ un = ⁴ C ₃ 2 un ³

=> ⁴ C ₃ 2 ³ un = ⁴ C ₃ 2 un ³

=> 8a = 2a ³

=> 2a (a − 4) = 0

=> a = 0 o a = 4

Por lo tanto, el valor de a es 0 o 4.

Pregunta 35. Si el término libre de x en la expansión de 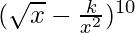$(\sqrt{x}-\frac{k}{x^2})^{10}$ es 405, encuentre el valor de k.

Solución:

Tenemos, $(\sqrt{x}-\frac{k}{x^2})^{10}$

El término general de esta expresión será,

Tr ₊₁ = $^{10}C_r(\sqrt{x})^{10-r}(-\frac{k}{x^2})^{r}$

= $^{10}C_r.(x)^{\frac{10-r}{2}-2r}(-k)^r$

Si el término es independiente de x , debemos tener,

=> $\frac{10-r}{2}-2r=0$

=> 10 − r − 4r = 0

=> 5r = 10

=> r = 2

Por lo tanto, el término requerido es el 3er ^término .

Entonces tenemos,

=> $^{10}C_2(\sqrt{x})^{10-2}(-\frac{k}{x^2})^{2}$ = 405

=> $^{10}C_2(\sqrt{x})^{8}(\frac{k^2}{x^4})$ = 405

=> $^{10}C_2(x^{4})(\frac{k^2}{x^4})$ = 405

=> $\frac{10×9}{2×1}×k^2$ = 405

=> 45k ² = 405

=> k2 = ⁹

=> k = 3

Por lo tanto, el valor de k es 3.

Pregunta 36. Encuentra el sexto término en la expansión (y ^1/2 + x ^1/3 ) ⁿ , si el coeficiente binomial del tercer término desde el final es 45.

Solución:

Tenemos, (y + x) ⁿ

El tercer término de la expansión desde el final es (n + 1 − 3 + 1) ^th term = (n − 1) ^th term.

=> T _n-1 = T _n-2+1 = norte C ⁿ_-2 (y ^1/2 ) ^n-(n-2) (x ^1/3 ) ^n-2

Se da el coeficiente de este término, es decir, 45.

=> ⁿ C _n-2 = 45

=> n (n − 1)/2 = 45

=> norte (norte – 1) = 90

=> norte ² – norte – 90 = 0

=> norte ² − 10n + 9n − 90 = 0

=> n(n−10) + 9 (n−10) = 0

=> n = 10 o n = −9 (ignorado)

Entonces, el sexto término de la expansión es T ₆ = T ₅₊₁

= ¹⁰ C _10-5 (y ^1/2 ) ^10-(10-5) (x ^1/3 ) ^10-5

= ¹⁰ C ₅ (y ^1/2 ) ⁵ (x ^1/3 ) ⁵

= 252 (y ^5/2 ) (x ^5/3 )

Pregunta 37. Si p es un número real y si el término medio en la expansión de (p/2 + 2) ⁸ es 1120, encuentra p.

Solución:

Tenemos, (p/2 + 2) ⁸

El número total de términos es 8 + 1 = 9 (número impar).

El término medio es (9+1)/2 = 5to término.

Por lo tanto, obtenemos T ₅ = T ₄₊₁ =1120

=> ⁸ C ₄ (p/2) ^8-4 (2) ⁴ = 1120

=> 70 (p/2) ⁴ (2) ⁴ = 1120

=> 70p ⁴ = 1120

=> pag ⁴ = 16

=> pag ⁴ = 2 ⁴

=> p = 2

Por lo tanto, el valor de p es 2.

Pregunta 38. Encuentra n en el binomio $(\sqrt[2]2+\frac{1}{\sqrt[3]3})^n$ , si la razón del 7º término desde el principio hasta el final es 1/6.

Solución:

Tenemos, $(\sqrt[2]2+\frac{1}{\sqrt[3]3})^n$

^{El 7mo} término desde el principio es $^nC_6(\sqrt[3]2)^{n-6}(\frac{1}{\sqrt[3]3})^6$ .

Y el séptimo ^término desde el final es $^nC_{n-6}(\sqrt[3]2)^{6}(\frac{1}{\sqrt[3]3})^{n-6}$ .

De acuerdo con la pregunta, tenemos,

=> $\frac{^nC_6(\sqrt[3]2)^{n-6}(\frac{1}{\sqrt[3]3})^6}{^nC_{n-6}(\sqrt[3]2)^{6}(\frac{1}{\sqrt[3]3})^{n-6}}=\frac{1}{6}$

=> $(\sqrt[3]2)^{n-12}(\frac{1}{\sqrt[3]3})^{12-n}=\frac{1}{6}$

=> $(\sqrt[3]2)^{n-12}(\sqrt[3]3)^{n-12}=\frac{1}{6}$

=> $(6)^{\frac{n-12}{3}}=6^{-1}$

=> (n − 12)/3 = −1

=> norte − 12 = −3

=> norte = 9

Por lo tanto, el valor de n es 9.

Pregunta 39. Si el séptimo término desde el principio y el final en la expansión binomial de $(\sqrt[2]2+\frac{1}{\sqrt[3]2})^n$ son iguales, encuentra n.

Solución:

Tenemos, $(\sqrt[2]2+\frac{1}{\sqrt[3]2})^n$

^{El 7mo} término desde el principio es $^nC_6(\sqrt[3]2)^{n-6}(\frac{1}{\sqrt[3]2})^6$ .

Y el séptimo ^término desde el final es $^nC_{n-6}(\sqrt[3]2)^{6}(\frac{1}{\sqrt[3]2})^{n-6}$ .

De acuerdo con la pregunta, tenemos,

=> $^nC_6(\sqrt[3]2)^{n-6}(\frac{1}{\sqrt[3]2})^6 = \hspace{0.1cm}^nC_{n-6}(\sqrt[3]2)^{6}(\frac{1}{\sqrt[3]2})^{n-6}$

=> $(\sqrt[3]2)^{n-12}=(\sqrt[3]2)^{12-n}$

=> norte – 12 = 12 – norte

=> 2n = 24

=> norte = 12

Por lo tanto, el valor de n es 12.

Publicación traducida automáticamente

Artículo escrito por gurjotloveparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 11 Soluciones RD Sharma – Capítulo 18 Teorema del binomio – Ejercicio 18.2 | conjunto 3

Pregunta 27. Si los términos 3 ^,⁴ , 5 ^y 6 ^en el desarrollo de (x + α) ⁿ son respectivamente a, b, c y d, demuestre que $\frac{b^2-ac}{c^2-bd}=\frac{5a}{3c}$ .

Pregunta 28. Si los términos 6 ^,⁷ , 8 ^y 9 ^en el desarrollo de (x + α) ⁿ son respectivamente a, b, c y d, demuestre que $\frac{b^2-ac}{c^2-bd}=\frac{4a}{3c}$ .

Pregunta 29. Si los coeficientes de tres términos consecutivos en la expansión de (1+x) ⁿ son respectivamente 76 , 95 y 76, encuentre n.

Pregunta 30. Si el 6 ^,⁷ y 8 en la ^expansión de (x + a) ⁿ son respectivamente 112, 7 y 1/4, encuentre x, a y n.

Pregunta 31. Si el ^2º , ^3º y 4º en la ^expansión de (x + a) ⁿ son respectivamente 240, 720 y 1080 respectivamente, encuentre x, a y n.

Pregunta 32. Encuentra a, b y n en la expansión de (a+b) ⁿ si los primeros tres términos son 729, 7290 y 30375 respectivamente.

Pregunta 33. Encuentra a, si los coeficientes de x ² y x ³ en la expansión de (3+ax) ⁹ son iguales.

Pregunta 34. Encuentra a, si los coeficientes de x y x ³ en la expansión de (2+ax) ⁴ son iguales.

Pregunta 35. Si el término libre de x en la expansión de $(\sqrt{x}-\frac{k}{x^2})^{10}$ es 405, encuentre el valor de k.

Pregunta 36. Encuentra el sexto término en la expansión (y ^1/2 + x ^1/3 ) ⁿ , si el coeficiente binomial del tercer término desde el final es 45.

Pregunta 37. Si p es un número real y si el término medio en la expansión de (p/2 + 2) ⁸ es 1120, encuentra p.

Pregunta 38. Encuentra n en el binomio $(\sqrt[2]2+\frac{1}{\sqrt[3]3})^n$ , si la razón del 7º término desde el principio hasta el final es 1/6.

Pregunta 39. Si el séptimo término desde el principio y el final en la expansión binomial de $(\sqrt[2]2+\frac{1}{\sqrt[3]2})^n$ son iguales, encuentra n.

Deja una respuesta Cancelar la respuesta

Pregunta 27. Si los términos 3 , 4 , 5 y 6 en el desarrollo de (x + α) n son respectivamente a, b, c y d, demuestre que .

Pregunta 28. Si los términos 6 , 7 , 8 y 9 en el desarrollo de (x + α) n son respectivamente a, b, c y d, demuestre que .

Pregunta 29. Si los coeficientes de tres términos consecutivos en la expansión de (1+x) n son respectivamente 76 , 95 y 76, encuentre n.

Pregunta 30. Si el 6 , 7 y 8 en la expansión de (x + a) n son respectivamente 112, 7 y 1/4, encuentre x, a y n.

Pregunta 31. Si el 2º , 3º y 4º en la expansión de (x + a) n son respectivamente 240, 720 y 1080 respectivamente, encuentre x, a y n.

Pregunta 32. Encuentra a, b y n en la expansión de (a+b) n si los primeros tres términos son 729, 7290 y 30375 respectivamente.

Pregunta 33. Encuentra a, si los coeficientes de x 2 y x 3 en la expansión de (3+ax) 9 son iguales.

Pregunta 34. Encuentra a, si los coeficientes de x y x 3 en la expansión de (2+ax) 4 son iguales.

Pregunta 35. Si el término libre de x en la expansión de es 405, encuentre el valor de k.

Pregunta 36. Encuentra el sexto término en la expansión (y 1/2 + x 1/3 ) n , si el coeficiente binomial del tercer término desde el final es 45.

Pregunta 37. Si p es un número real y si el término medio en la expansión de (p/2 + 2) 8 es 1120, encuentra p.

Pregunta 38. Encuentra n en el binomio , si la razón del 7º término desde el principio hasta el final es 1/6.

Pregunta 39. Si el séptimo término desde el principio y el final en la expansión binomial de son iguales, encuentra n.

Deja una respuesta Cancelar la respuesta

Pregunta 27. Si los términos 3 ^,⁴ , 5 ^y 6 ^en el desarrollo de (x + α) ⁿ son respectivamente a, b, c y d, demuestre que $\frac{b^2-ac}{c^2-bd}=\frac{5a}{3c}$ .

Pregunta 28. Si los términos 6 ^,⁷ , 8 ^y 9 ^en el desarrollo de (x + α) ⁿ son respectivamente a, b, c y d, demuestre que $\frac{b^2-ac}{c^2-bd}=\frac{4a}{3c}$ .

Pregunta 29. Si los coeficientes de tres términos consecutivos en la expansión de (1+x) ⁿ son respectivamente 76 , 95 y 76, encuentre n.

Pregunta 30. Si el 6 ^,⁷ y 8 en la ^expansión de (x + a) ⁿ son respectivamente 112, 7 y 1/4, encuentre x, a y n.

Pregunta 31. Si el ^2º , ^3º y 4º en la ^expansión de (x + a) ⁿ son respectivamente 240, 720 y 1080 respectivamente, encuentre x, a y n.

Pregunta 32. Encuentra a, b y n en la expansión de (a+b) ⁿ si los primeros tres términos son 729, 7290 y 30375 respectivamente.

Pregunta 33. Encuentra a, si los coeficientes de x ² y x ³ en la expansión de (3+ax) ⁹ son iguales.

Pregunta 34. Encuentra a, si los coeficientes de x y x ³ en la expansión de (2+ax) ⁴ son iguales.

Pregunta 35. Si el término libre de x en la expansión de $(\sqrt{x}-\frac{k}{x^2})^{10}$ es 405, encuentre el valor de k.

Pregunta 36. Encuentra el sexto término en la expansión (y ^1/2 + x ^1/3 ) ⁿ , si el coeficiente binomial del tercer término desde el final es 45.

Pregunta 37. Si p es un número real y si el término medio en la expansión de (p/2 + 2) ⁸ es 1120, encuentra p.

Pregunta 38. Encuentra n en el binomio $(\sqrt[2]2+\frac{1}{\sqrt[3]3})^n$ , si la razón del 7º término desde el principio hasta el final es 1/6.

Pregunta 39. Si el séptimo término desde el principio y el final en la expansión binomial de $(\sqrt[2]2+\frac{1}{\sqrt[3]2})^n$ son iguales, encuentra n.