Pregunta 11. Encuentra la suma de todos los números enteros entre 100 y 550 que son divisibles por 9.
Solución:
segun pregunta
PA = 108, 117…549
a(primer término) = 108, d(diferencia común) = 9, a n (n-ésimo término) = 549
un norte = un + ( n – 1)d
549 = 108 + (n – 1)(9)
441 = 9n – 9
450 = 9n
norte = 50
S = n/2 [2a + (n -1)d]
S = 50/2 [2(108) + (50 – 1)(9)]
= 25 [216 + (49)(9)]
= 25 [216 + 441]
= 25 [657]
= 16425
Por lo tanto, la suma de todos los números enteros entre 100 y 550 que son divisibles por 9 = 16425
Pregunta 12. Encuentra la suma de la serie:
3 + 5 + 7 + 6 + 9 + 12 + 9 + 13 + 17 + … a 3n términos.
Solución:
AP = 3 +5 +7 + 9 + … a 3n
a = 3, d = 2, n = 3n
S = n/2 [2a + (n – 1)d]
= 3n/2 [2(3) + (3n – 1)(2)]
= 3n [3 + (3n – 1)]
= 3n [3n + 2]
Por lo tanto, la suma de los AP dados = 3n [3n + 2]
Pregunta 13. Encuentra la suma de todos aquellos números enteros entre 100 y 800 cada uno de los cuales al dividir por 16 deja el resto 7.
Solución:
segun pregunta
AP = 103, 119,…,791
a = 103, l = 791
un norte = un + ( n – 1)d
791 = 103 + (n – 1)16
norte = 44
S = n/2 [a + l]
S = 44/2 [103 + 791]
= 22 [894]
= 19668
Por lo tanto, la suma de todos los números enteros entre 100 y 800
cada uno de los cuales al dividir por 16 deja el resto 7 = 19668
Pregunta 14. Resuelve:
(i) 25 + 22 + 19 + 16 + … + x = 115
(ii) 1 +4+7+ 10 + … + x = 590
Solución:
(i) Ap= 25 + 22 + 19 + 16 +…+x = 115
a = 25, d = -3, S = 115
Usando la fórmula
S = n/2[2a + (n – 1)d]
⇒ 115 = n/2 [2 x 25+ (n – 1)(-3)]
⇒ 115 x 2 = n[50 – 3n + 3]
⇒ 230 = n(53 – 3n)
⇒ 230 = 53n – 3n 2
⇒ 3n 2 – 53n + 230 = 0
Usando fórmula cuadrática:
Ahora, pon el valor de a = 3, b = – 53 y c = 230, obtenemos
n = 46/6,10
⇒ n = 10 cuando n ≠ 46/6
Entonces, a n = x = a + (n – 1)d
⇒ x = 25 + (10 – 1)(-3)
⇒ x = 25 – 27 = -2
Por lo tanto, el valor de x = -2
(ii) PA = 1 + 4 + 7 + 10 +….+ x = 590
a = 1, d = 3
Usando la fórmula
S = n/2 [2a + (n – 1)d]
⇒ 590 = n/2[2 x 1 + (n – 1)(3)]
⇒ 590 x 2 = n[2 + 3n – 3]
⇒ 1180 = n(3n – 1)
⇒ 1180 = 3n 2 – n
⇒ 3n 2 – n -1180 = 0
Usando fórmula cuadrática:
Ahora, pon el valor de a = 3, b = – 1 y c = -1180, obtenemos
n = -118/6, 20
⇒ n = 20, ya que n ≠ -118/6
un norte = x = un + (n – 1) d
⇒ x = 1 + (20 – 1)(3)
⇒ x = 1 + 60 – 3 = 58
Por lo tanto, el valor de x = 58
Pregunta 15. Encuentra el r -ésimo término de un AP, la suma de cuyos primeros n términos es 3n 2 + 2n.
Solución:
Según la pregunta
Como, S n = 3n 2 + 2n
Entonces, a = S 1 = 3 x 1 2 + 2 x 1 = 3 + 2 = 5 y
S 2 = 3 x 2 2 +2 x 2 = 12+4 = 16
⇒ a + a2 = 16
⇒ a + a + d = 16
⇒ 2a + d = 16
⇒ 2 x 5 + d = 16
⇒ re = 16 – 10
⇒ re = 6
Ahora,
una r = una + (r – 1)d
= 5+ (r -1) x 6
= 5 + 6r – 6
Por lo tanto, el a r = 6r – 1
Pregunta 16. ¿Cuántos términos hay en el AP cuyo primer y quinto término son -14 y 2 respectivamente y la suma de los términos es 40?
Solución:
Según la pregunta tenemos
a = -14 y S n = 40 ………………………. (i)
un 5 = 2
Mediante el uso de la fórmula
⇒ a + (5 – 1)d = 2
⇒ -14 + 4d = 2
⇒ 4d = 16
⇒ d = 4 …………………………..(ii)
Mediante el uso de la fórmula
S norte = n /2 [2a + (n – 1) d]
⇒ 40 = n/2 [2(-14) + (n – 1) x 4] (De la ecuación (i) y (ii))
⇒ 80 = n[-28 + 4n – 4]
⇒ 80 = 4n 2 – 32n
⇒ n 2 – 8n – 20 = 0
⇒ (n -10)(n + 2) = 0
⇒ n = 10, -2
Pero n no puede ser negativo.
Por lo tanto, el número total de términos en el AP = 10
Pregunta 17. La suma de los primeros 7 términos de un AP es 10 y la de los siguientes 7 términos es 17. Encuentra la progresión.
Solución:
Según la pregunta tenemos
S 7 = 10
Mediante el uso de la fórmula
S norte = n /2 [2a + (n – 1) d]
⇒ 7/2 [2a + (7 – 1)d] = 10
⇒ 7/2 [2a + 6d] = 10
⇒ a + 3d = 10/7 ………………………………… (yo)
Además, la suma de los siguientes siete términos = S 14 – S 7 = 17
⇒ 14/2 [2a + (14 – 1)d] – 7/2 [2a + (7 – 1)d] = 17
⇒ 7[2a + 13d] – 7/2[2a + 6d] = 17
14a + 91d – 7a – 21d = 17
7a + 70d = 17
a + 10d = 17/7 ………………………………….. (ii)
De la ecuación (i) y (ii), obtenemos:
10/7 – 3 días = 17/7 – 10 días
⇒ 7d = 1
⇒ re = 1/7
Al poner el valor en la ecuación (i), obtenemos:
a + 3d = 10/7
⇒ a+ 3/7 = 10/7
⇒ a = 1, d = 1/7
Por tanto, la progresión = 1, 8/7, 9/7, 10/7…
Pregunta 18. El tercer término de un AP es 7 y el séptimo término excede tres veces el tercer término en 2. Encuentra el primer término, la diferencia común y la suma de los primeros 20 términos.
Solución:
Según la pregunta tenemos
un 3 = 7, un 7 – 3un 3 = 2
Mediante el uso de la fórmula
un norte = un + ( n – 1)d
⇒ a + (3 – 1)d = 7
⇒ a + 2d = 7 …………………………………… (yo)
También,
un 7 – 3a 3 = 2
⇒ a 7 – 21 = 2 (Dado)
⇒ a + (7 – 1)d = 23
⇒ a + 6d = 23 ………………………………………. (ii)
De la ecuación (i) y (ii), obtenemos
4d = 16
⇒ re = 4
Al poner el valor en la ecuación (i), obtenemos
un + 2 (4) = 7
un = -1
Mediante el uso de la fórmula
S norte = n /2 [2a + (n – 1) d]
S 20 = 20/2 [2(-1) + (20-1)(4)]
⇒ S 20 = 10[-2 + 76]
⇒ S 20 = 10[74] = 740
Por eso,
a = -1, d = 4, S 20 = 740
Pregunta 19. El primer término de un AP es 2 y el último término es 50. La suma de todos estos términos es 442. Encuentra la diferencia común.
Solución:
Según la pregunta tenemos
a = 2, l = 50, S n = 442
Ahora, S n = 442
⇒ n/2[a + l] = 442
⇒ n/2 [2 + 50] = 442
⇒ n = 17
un 17 = 50
Al usar la fórmula, obtenemos
⇒ a + (17 – 1) d = 50
⇒ 2 + 16d = 50
⇒ re = 3
Pregunta 20. El número de términos de un AP es par; la suma de los términos impares es 24, la de los términos pares es 30 y el último término excede al primero en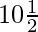 
, encuentre el número de términos y la serie.
Solución:
Según la pregunta, tenemos
a 1 + a 3 +… +a 2n-1 = 24 ……………..(1)
a 2 + a 4 +… +a 2n = 30 ……………..(2)
Ahora, restando la ecuación (1) de (2), obtenemos:
(d + d+…+ hasta n términos) = 6
⇒ n = 6 ………….(3)
Dado :
un 2n = un 1 + 21/2
⇒ un 2n – un 1 = 21/2
⇒ a + (2n – 1)d – a = 21/2 [a 2n = a + (2n – 1)d, a 1 = a]
⇒ 2º – d = 21/2
⇒ 2 x 6 – d = 21/2 (De la ecuación (3))
⇒ re = 3/2
Al poner el valor en la ecuación (3), obtenemos
norte = 4
⇒ 2n = 8
Por lo tanto, hay 8 términos en la progresión.
Para encontrar el valor del primer término:
un 2 + un 4 +…+un 2n = 30
⇒ (a + d) + (a + 3d)+… +[a + (2n – 1)d] = 30
⇒ n/2 [(a + d) + a + (2n – 1)d] = 30
Al poner n = 4 y d = 3/2, obtenemos
un = 3/2
Por lo tanto, la serie será 1, 1/2, 3,
…
Pregunta 21. Si S n = n 2 p y S m = m 2 p, m ≠ n, en un AP, demuestre que S p = p 3 .
Solución:
S norte = norte 2 pags
⇒ n/2 [2a + (n – 1)d] = n 2 p
⇒ 2np = 2a + (n – 1)d ………………. (i)
S metro = metro 2 pags
⇒ n/2 [2a + (m – 1)d] = m 2 p
⇒ 2mp = 2a + (m – 1)d ……………….. (ii)
Al restar la ecuación (ii) de la ecuación (i), obtenemos
2p(n-m) = (n-m)d
2p = d ………………..(iii)
Al sustituir el valor en la ecuación (i), obtenemos
n = 2a + (n – 1)d
⇒ segundo – segundo + re = 2a
⇒ a = d/2 = p [de la ecuación (iii)] ……………….(iv)
Sp = p /2[2a + (p – 1)d]
⇒ Sp = p/2[2p + (p – 1)2p ]
⇒ S p = p/2[2p + 2p 2 -2p]
⇒ Sp = p/2[ 2p 2 ]
⇒ S pag = pag 3
Por lo tanto probado
Pregunta 22. Si el término 12 de un AP es -13 y la suma de los primeros cuatro términos es 24, ¿cuál es la suma de los primeros 10 términos?
Solución:
Consideremos primer término = a y diferencia común = d
Dado que a 12 = -13
Usando la fórmula
⇒ a + (12 – 1)d = -13
⇒ a + 11d = -13 ………………. (i)
Además, S 4 = 24 (dado)
Usando la fórmula
⇒ 4/2 [2a + (4 – 1)d] = 24
⇒ 2(2a + 3d) = 24
⇒ 2a + 3d = 12 ………………. (ii)
De la ecuación (i) y (ii), obtenemos
19d = -38
d = -2
Ahora pon el valor de d en la ecuación (i), obtenemos
a + 11(-2) = -13
⇒ un = 9
S 10 = 10/2 [(2)(9) + (10 – 1)(-2)]
⇒ S 10 = 5[18 – 18] = 0
Por lo tanto, la suma de los primeros diez términos = 0
Publicación traducida automáticamente
Artículo escrito por manandeep1610 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA