Pregunta 1. Encuentra la suma de las siguientes series hasta el infinito:
(i) 1 – 1/3 + 1/3 2 – 1/3 3 + 1/3 4 + … ∞
Solución:
La serie dada es un GP infinito con el primer término (a) = 1 y la razón común (r) = –1/3.
Sabemos que la suma de un GP hasta el infinito viene dada por S = a/(1 – r).
= 1/[1 – ( – 1/3)]
= 1/(4/3)
= 3/4
Por lo tanto, la suma de la serie hasta el infinito es 3/4.
(ii) 8 + 4√2 + 4 + …. ∞
Solución:
La serie dada es un GP infinito con el primer término (a) = 8 y la razón común (r) = 4√2/8 = 1/√2
Sabemos que la suma de un GP hasta el infinito viene dada por S = a/(1 – r).
= 8/[1 – (1/√2)]
= 8/[(√2 – 1)/√2]
= 8√2/(√2 – 1)
=
=
= 8(2 + √2)
Por tanto, la suma de la serie hasta el infinito es 8(2 + √2).
(iii) 2/5 + 3/5 2 + 2/5 3 + 3/5 4 + …. ∞
Solución:
La serie dada tiene suma, S = 2/5 + 3/5 2 + 2/5 3 + 3/5 4 + …. ∞
=> S = (2/5 + 2/5 3 + … ∞) + (3/5 2 + 3/5 4 + … ∞)
Sabemos que la suma de un GP hasta el infinito viene dada por S = a/(1–r).
Sea S 1 = 2/5 + 2/5 3 + … ∞
Este es un GP infinito con el primer término (a) = 2/5 y razón común (r) = 1/5 2 = 1/25.
Entonces, S 1 =
=
=
Sea S 2 = 3/5 2 + 3/5 4 + … ∞
Este es un GP infinito con el primer término (a) = 3/5 y razón común (r) = 1/5 2 = 1/25.
Entonces, S 2 =
=
=
Ahora, suma requerida, S = S 1 + S 2
=
= 13/24
Por lo tanto, la suma de la serie hasta el infinito es 13/24.
(iv) 10 – 9 + 8,1 – 7,29 + …. ∞
Solución:
La serie dada es un GP infinito con el primer término (a) = 10 y la razón común (r) = – 9/10
Sabemos que la suma de un GP hasta el infinito viene dada por S = a/(1 – r).
= 10/[1 – (–9/10)]
= 10/[1 + 9/10]
= 100/19
= 5.263
Por lo tanto, la suma de la serie hasta el infinito es 5.263.
(v) 1/3 + 1/5 2 + 1/3 3 + 1/5 4 + + 1/3 5 + 1/5 6 …. ∞
Solución:
La serie dada tiene suma, S = 1/3 + 1/5 2 + 1/3 3 + 1/5 4 + + 1/3 5 + 1/5 6 …. ∞
=> S = (1/3 + 1/3 3 + 1/3 5 … ∞) + (1/5 2 + 1/5 4 + 1/5 6 … ∞)
Sabemos que la suma de un GP hasta el infinito viene dada por S = a/(1–r).
Sea S 1 = 1/3 + 1/3 3 + 1/3 5 … ∞
Este es un GP infinito con el primer término (a) = 1/3 y la razón común (r) = 1/3 2 = 1/9.
Entonces, S 1 =
= 3/8
Sea S 2 = 1/5 2 + 1/5 4 + 1/5 6 … ∞
Este es un GP infinito con el primer término (a) = 1/5 2 y razón común (r) = 1/5 2 = 1/25.
Entonces, S 2 =
= 1/24
Ahora, suma requerida, S = S 1 + S 2
=
= 10/24
= 5/12
Por lo tanto, la suma de la serie hasta el infinito es 5/12.
Pregunta 2. Demuestra que:
Solución:
Podemos escribir el LHS como,
Tenemos S = 1/3 + 1/9 + 1/27 + . . . .∞
que forma un GP infinito con el primer término (a) = 1/3 y la razón común (r) = 1/3.
Además, la suma de un GP hasta el infinito viene dada por S = a/(1–r).
=
=
=
Entonces, LHS se convierte en, 9 S = 9 1/2 = 3 = RHS
Por lo tanto probado.
Pregunta 3. Demuestra que:
Solución:
El LHS se puede escribir como,
IZQ =
=
Tenemos, S = 1/4 + 2/8 + 3/16 + 4/32 + …∞. . . . . (1)
Dividiendo ambos lados por 2, obtenemos,
S/2 = 1/8 + 2/16 + 3/32 + …∞ . . . . (2)
Restando (2) de (1) obtenemos,
Ahora bien, este es un GP infinito con el primer término (a) = 1/4 y razón común (r) = 1/2.
Además, la suma de un GP hasta el infinito viene dada por a/(1–r).
=> S/2 = 1/2
=> S = 1
Entonces, LHS se convierte en, 2 S = 2 = RHS
Por lo tanto probado.
Pregunta 4. Si S p denota la suma de la serie 1 + r p + r 2p + … hasta ∞ y s p la suma de la serie 1 – r p + r 2p – … hasta ∞, demuestre que s p + S p = 2 S 2p .
Solución:
Sabemos que la suma de un GP hasta el infinito viene dada por S = a/(1 – r).
Entonces, S p = 1 + r p + r 2p + … a ∞
Este es un GP infinito con el primer término (a) = 1 y razón común (r) = r p .
Entonces, S p = 1/(1 – r p )
Además, s p = 1 – r p + r 2p – … a ∞
Esto es GP con el primer término (a) = 1 y razón común (r) = –r p .
Entonces, s p = 1/[1 – (-r p )] = 1/(1 + r p )
Por lo tanto, LHS = s p + S p
=
=
=
Ahora, RHS = 2 S 2p
=
= LHS
Por lo tanto probado.
Pregunta 5. Encuentra la suma de los términos de un GP decreciente infinito en el que todos los términos son positivos, el primer término es 4 y la diferencia entre el tercer y quinto término es igual a 32/81.
Solución:
Dado que GP tiene el primer término (a) = 4 y,
=> ar 4 – ar 2 = 32/81
=> 4(r 4 – r 2 ) = 32/81
=> r 2 (r 2 – 1) = 8/81
Supongamos que r 2 = x, por lo que la ecuación se convierte en,
=> x(x – 1) = 8/81
=> 81x 2 – 81x – 8 = 0
Resolviendo para x, obtenemos,
=>
=>
=> x = 1/9 o x = 8/9
Entonces, r 2 = 1/9 o r 2 = 8/9
=> r = 1/3 o r = 2√2/3
Sabemos que la suma de un GP hasta el infinito viene dada por S = a/(1 – r).
Cuando a = 4 y r = 1/3,
S = 4/(1 – (1/3))
= 4/(2/3)
= 6
Cuando a = 4 y r = 2√2/3,
S = 4/[1 – (2√2/3)]
= 12/(3 – 2√2)
Pregunta 6. Exprese el decimal periódico 0.125125125… como un número racional.
Solución:
Nos dan, 0,125125125 = 0,125 + 0,000125 + 0,000000125 +…
= 125/10 3 + 125/10 6 + 125/10 9 + …
Este es un GP infinito con el primer término (a) = 125/10 3 y razón común (r) = 1/10 3 = 1/1000.
Sabemos que la suma de un GP hasta el infinito viene dada por S = a/(1 – r).
S =
=
=
Por lo tanto, el decimal periódico 0,125125125 se puede expresar en número racional como 125/999.
Pregunta 7. Encuentra el número racional cuya expansión decimal es 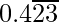
Solución:
Nos dan,
= 0.4 + 0.0232323 . . . . . .
= 0,4 + 0,023 + 0,00023 + 0,0000023 . . . .
= 0,4 + 23/10 3 + 23/10 5 + 23/10 7 + . . . .
Tenemos, S = 23/10 3 + 23/10 5 + 23/10 7 + . . . .
Este es un GP infinito con el primer término (a) = 23/10 3 y razón común (r) = 1/10 2 = 1/100.
Sabemos que la suma de un GP hasta el infinito viene dada por S = a/(1 – r).
S =
=
=
Por lo tanto, el número racional se convierte en,
=
=
Por lo tanto, 419/990 es el número racional para esta expansión decimal.
Pregunta 8. Encuentra los números racionales que tienen las siguientes expansiones decimales:
(i) 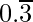
Solución:
Tenemos,
= 0.3333…
= 0,3 + 0,33 + 0,333 + . . . .
= 3/10 + 3/10 2 + 3/10 3 + . . . .
Este es un GP infinito con el primer término (a) = 3/10 y la razón común (r) = 1/10.
Sabemos que la suma de un GP hasta el infinito viene dada por S = a/(1–r).
=
=
=
Por lo tanto, 1/3 es el número racional para esta expansión decimal.
(ii) 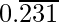
Solución:
Tenemos,
= 0.231231231
= 0,231 + 0,000231 + 0,000000231 + . . . .
= 231/10 3 + 231/10 6 + 231/10 9 + . . . .
Este es un GP infinito con el primer término (a) = 231/10 3 y razón común (r) = 1/10 3 = 1/1000.
Sabemos que la suma de un GP hasta el infinito viene dada por S = a/(1 – r).
=
=
=
Por lo tanto, 231/999 es el número racional para esta expansión decimal.
(iii) 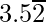
Solución:
Tenemos,
= 3.522222
= 3,5 + 0,02 + 0,002 + 0,0002 + . . . .
= 3,5 + (2/10 2 + 2/10 3 + 2/10 4 + . . . )
Tenemos, S = 2/10 2 + 2/10 3 + 2/10 4 + . . .
Este es un GP infinito con el primer término (a) = 2/10 2 y razón común (r) = 1/10.
Sabemos que la suma de un GP hasta el infinito viene dada por S = a/(1 – r).
Entonces, S =
=
=
Por lo tanto, el número se convierte en,
=
=
Por lo tanto, 317/90 es el número racional para esta expansión decimal.
(iv) 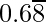
Solución:
Tenemos,
= 0.68888
= 0,6 + 0,08 + 0,888 + 0,8888 + . . . .
= 0,6 + (8/10 2 + 8/10 3 + 8/10 4 + . . . .)
Tenemos, S = 8/10 2 + 8/10 3 + 8/10 4 + . . . .
Este es un GP infinito con el primer término (a) = 8/10 2 y razón común (r) = 1/10.
Sabemos que la suma de un GP hasta el infinito viene dada por S = a/(1 – r).
S =
=
=
Por lo tanto, el número se convierte en,
=
=
Por lo tanto, 31/45 es el número racional para esta expansión decimal.
Pregunta 9. Un lado de un triángulo equilátero mide 18 cm. Los puntos medios de sus lados se unen para formar otro triángulo cuyos puntos medios, a su vez, se unen para formar otro triángulo más. El proceso se continúa infinitamente. Encuentre la suma de:
(i) perímetros de todos los triángulos.
Solución:
Los lados de todos estos triángulos forman un GP infinito, 18, 9, 9/2, . . . .
Su primer término es primer término (a) = 18 y razón común (r) = 9/18 = 1/2
Sabemos que la suma de un GP hasta el infinito viene dada por S = a/(1 – r).
Por lo tanto, S = 18/[1 – 1/2]
= 18/(1/2)
= 36
Ahora, suma de perímetros de todos los triángulos, S p = 3a 1 + 3a 2 + 3a 3 + . . . .,
donde a 1 ,a 2 ,a 3 , . . . son los lados de estos triángulos.
= 3 (un 1 + un 2 + un 3 + . . . .)
= 3S
= 3(36)
= 108
Por tanto, la suma de los perímetros de todos los triángulos es 108 cm.
(ii) áreas de todos los triángulos.
Solución:
Suma de las áreas de todos los triángulos,
=
Aquí la serie 324 + 81 + (81/4)+. . .
forma un GP infinito con el primer término (a) = 324 y la razón común (r) = 81/324 = 1/4.
Sabemos que la suma de un GP hasta el infinito viene dada por S = a/(1–r).
Entonces, Sa =
=
= 108√3
Por lo tanto, la suma de las áreas de todos los triángulos es 108√3 cm 2 .
Pregunta 10. Encuentra un GP infinito cuyo primer término sea 1 y cada término sea la suma de todos los términos que le siguen.
Solución:
Dado el primer término de GP(a) = 1 y,
un norte = un norte+1 + un norte+2 + un norte+3 + . . . .
Sabemos que el término n de un GP está dado por a n = ar n-1 . Entonces, obtenemos,
=> ar norte–1 = ar norte + ar norte+1 + ar norte+2 + . . . .
=> ar n-1 = ar norte (1 + r + r 2 + . . . .)
=> (1 + r + r 2 + . . . .) = 1/r
Aquí la serie en LHS forma un GP infinito con el primer término (a) = 1 y la razón común (r) = r.
Sabemos que la suma de un GP hasta el infinito viene dada por S = a/(1 – r).
=> 1/(1 – r) = 1/r
=> 2r = 1
=> r = 1/2
Como el primer término (a) es 1 y la razón común es 1/2, el GP infinito requerido es,
1, 1/2, 1/4, 1/8, . . .
Pregunta 11. La suma de los dos primeros términos de un GP infinito es 5 y cada término es tres veces la suma de los términos sucesivos. Encuentra el médico de cabecera
Solución:
Dado a + ar = 5 => a(1 + r) = 5 . . . . (1)
Además, un n = 3(un n+1 + un n+2 + un n+3 + . . . .)
Sabemos que el término n de un GP está dado por a n = ar n-1 . Entonces, obtenemos,
=> arn -1 = 3(arn + arn + 1 + arn +2 + . . . .)
=> ar n-1 = 3ar n (1 + r + r 2 + . . . .)
=> (1 + r + r 2 + . . . .) = 1/3r
Aquí la serie en LHS forma un GP infinito con el primer término (a) = 1 y la razón común (r) = r.
Sabemos que la suma de un GP hasta el infinito viene dada por S = a/(1 – r).
=> 1/(1 – r) = 1/3r
=> 4r = 1
=> r = 1/4
De (1), obtenemos, a(1 + 1/4) = 5
=> un(5/4) = 5
=> un = 4
Como el primer término (a) es 4 y la razón común es 1/4, el GP infinito requerido es,
4, 1, 1/4, 1/16, . . . .
Pregunta 12. Muestre que en un GP infinito con razón común r (|r| < 1), cada término tiene una razón constante a la suma de todos los términos que le siguen.
Solución:
De acuerdo con la pregunta, tenemos,
=
=
Aquí la serie en el denominador forma un GP infinito con el primer término (a) = 1 y la razón común (r) = r.
Sabemos que la suma de un GP hasta el infinito viene dada por S = a/(1–r). Entonces nuestra expresión se convierte en,
=
=
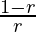
Dado que la relación común (r) del GP permanece constante, el valor de la relación
también permanece constante.
Por lo tanto, en un GP infinito, cada término tiene una relación constante con la suma de todos los términos que le siguen.
Pregunta 13. Si S denota la suma de un GP infinito, S 1 denota la suma de los cuadrados de sus términos, entonces demuestre que el primer término y la razón común son respectivamente 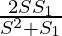 y
y 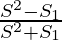
Solución:
Sabemos que la suma de un GP hasta el infinito viene dada por S = a/(1 – r).
Aquí, S = a + ar + ar 2 + ar 3 + . . . . = a/(1 – r) . . . . (1)
También dado que S 1 = a 2 + a 2 r 2 + a 2 r 4 + a 2 r 6 + . . . . = un 2 /(1 – r 2 ) . . . . (2)
Elevando al cuadrado ambos lados de (1), obtenemos,
=>
De la ecuación (2), obtenemos,
=>
=>
=> S 2 – S 2 r = S 1 + S 1 r
=> (S 1 + S 2 )r = S 2 − S 1
=> r =
Al poner el valor de r en la ecuación (1), obtenemos
=> a = S(1 − r)
=> un =
=> un =
=> un =
Por lo tanto probado.
Publicación traducida automáticamente
Artículo escrito por gurjotloveparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
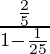
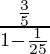
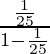
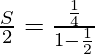
![Rendered by QuickLaTeX.com \frac{125}{10^3}\left[\frac{1}{1-\frac{1}{1000}}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-07cc12ae6e104d1c3f13bd17ce80f6d1_l3.png)
![Rendered by QuickLaTeX.com \frac{23}{10^3}\left[\frac{1}{1-\frac{1}{100}}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-971734ead554e14fc2c5bf988c73ea7c_l3.png)
![Rendered by QuickLaTeX.com \frac{3}{10}\left[\frac{1}{1-\frac{1}{10}}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b50682ecc182de3589033ab503cbee7a_l3.png)
![Rendered by QuickLaTeX.com \frac{231}{1000}\left[\frac{1}{1-\frac{1}{1000}}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-66099f377f536599754dcc7a2b4b8bd0_l3.png)
![Rendered by QuickLaTeX.com \frac{2}{100}\left[\frac{1}{1-\frac{1}{10}}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6c884af1c7af03808115297b03c32ca3_l3.png)
![Rendered by QuickLaTeX.com \frac{8}{100}\left[\frac{1}{1-\frac{1}{10}}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-dbd04ae0cc26909750b5d98f365f1a55_l3.png)
![Rendered by QuickLaTeX.com \frac{\sqrt{3}}{4}\left[\frac{1}{1-\frac{1}{4}}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-725c8766afb10cf9f03d3bd8ba8b8dec_l3.png)