Pregunta 12. Si (a – b), (b – c), (c – a) están en GP, entonces demuestre que (a + b + c) 2 = 3(ab + bc + ca)
Solución:
Dado: (a – b), (b – c), (c – a) están en GP
(b – c) 2 = (a – b)(c – a)
b 2 + c 2 – 2bc = ac – a 2 – bc + ab
b 2 + c 2 + a 2 = ac + bc + ab -(1)
Ahora,
(a + b + c) 2 = a 2 + b 2 + c 2 + 2ab + 2bc + 2ca
= ac + bc + ab + 2ab + 2bc + 2ca
Entonces, usando la ecuación (1), obtenemos
= 3ab + 3bc + 3ca
(a + b + c) 2 = 3(ab + bc + ca)
LHS = RHS
Por lo tanto, demostrado
Pregunta 13. Si a, b, c están en GP, entonces demuestre que:
Solución:
Dado: a, b, c están en GP
Entonces, a, b = ar, c = ar 2
1/r = 1/r
LHS = RHS
Por lo tanto, demostrado
Pregunta 14. Si los términos 4 , 10 y 16 de un GP son x, y y z respectivamente. Demostrar que x, y, z están en GP
Solución:
Consideremos el 4 ° término = ar 3
10 ° término = ar 9
16 o término = ar 15
Entonces, ar 9 =
= ar 9
Por lo tanto, los términos 4 , 10 y 16 también están en GP
Por lo tanto, demostrado
Pregunta 15. Si a, b, c están en AP y a, b, d están en GP, entonces demuestre que a, a – b, d – c están en GP
Solución:
Dado: a, b, c están en AP
2b = a + c -(1)
además,
a, b, d están en GP, entonces
b 2 = anuncio -(2)
Ahora,
(a – b) 2 = a 2 + b 2 – 2ab
= a 2 + ad – a(a + c)
De la ecuación (1) y (2), obtenemos
= a 2 + ad – a 2 – ac
= anuncio – ac
(a – b) 2 = a(d – c)
(a – b)/a = (d – c)/(a – b)
Por lo tanto, demostrado a, (a – b), (d – c) están en GP
Pregunta 16. Si los términos p th , q th , r th y s th de un AP están en GP, entonces demuestre que p – q, q – r, r – s están en GP
Solución:
Consideremos que R es razón común,
Dado: a p , a q , a r , a s de AP están en GP
R =
Ahora,
Usando la ecuación (1) y (2), obtenemos
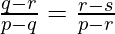
Por lo tanto, demostrado (p – q), (q – r), (r – s) están en GP
Pregunta 17. Si 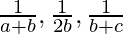 son los tres términos consecutivos de un AP, demuestre que a, b, c son los tres términos consecutivos de un GP
son los tres términos consecutivos de un AP, demuestre que a, b, c son los tres términos consecutivos de un GP
Solución:
Dado: \frac{1}{a+b},\frac{1}{2b},\frac{1}{b+c} están en AP
ab + ac + b 2 + bc = 2b 2 + bc + ba
b 2 + ac = 2b 2
b 2 = ca
Por lo tanto, se demostró que a, b, c están en GP
Pregunta 18. Si x a = x b/2 z b/2 = z c , entonces demuestre que 1/a, 1/b, 1/c están en AP
Solución:
b/2a + b/2c = 1
1/a + 1/c = 2/b
Por lo tanto, 1/a, 1/b, 1/c están en AP
Pregunta 19. Si a, b, c están en AP, b, c, d están en GP y 1/c, 1/d, 1/e están en AP, demuestre que a, c, e están en GP
Solución:
Dado: a, b, c están en AP
2b = a + c -(1)
Además, b, c, d están en GP
c 2 = bd -(2)
1/c, 1/d, 1/e están en AP
2/d = 1/c + 1/e -(3)
Necesitamos demostrar que
a, b, c están en GP
c2 = ae
Ahora,
do 2 (do + e) = as + do 2 e
do 3 + do 2 mi = as + do 2 mi
c 3 = as
c2 = ae
Por lo tanto, probado.
Pregunta 20. Si a, b, c están en AP y a, x, b y b, y, c están en GP, demuestre que x 2 , b 2 , y 2 están en AP
Solución:
Dado: a, b, c están en AP
2b = a + c -(1)
Además, a, x, b están en GP
x = ab-(2)
y b, y, c están en GP
y 2 = bc -(3)
Ahora
2b 2 = x 2 + y 2
= (ab) + (bc) -(Usando la ecuación (2) y (3))
2b 2 = b(a + c)
2b 2 = b(2b) -(Usando eq(1))
2b 2 = 2b 2
LHS = RHS
2b 2 = x 2 + y 2
Por lo tanto, x 2 , b 2 , y 2 están en AP
Pregunta 21. Si a, b, c están en AP y a, b, d están en GP, demuestre que a, (a – b), (d – c) están en GP
Solución:
Dado: a, b, c están en AP
2b = a + c -(1)
Además, a, b, d están en GP
b 2 = anuncio -(2)
Ahora
(a – b) 2 = a(d – c) -(Usando eq(2))
a 2 – 2ab = -ac
a 2 – 2ab = ab – ac
a(a-b) = a(b-c)
a-b = a-c
2b = a + c
a + c = a + c, -(Usando eq(1))
LHS = RHS
Por lo tanto, a, (a – b), (d – c) están en GP
Pregunta 22. Si a, b, c son tres números reales en GP y a + b + c = xb, entonces demuestre que x < -1 o x > 3.
Solución:
Consideremos que r es la razón común de GP
Entonces, a, b = ar, c = ar 2
a + b + c = xb
a + ar + ar 2 = x(ar)
a(1 + r + r 2 ) = x(ar)
r2 + (1 – x)r + 1 = 0
Aquí, r es real, entonces
D ≥ 0
(1 – x) 2 – 4(1)(1) ≥ 0
1 + x 2 -2x – 4 ≥ 0
x2 – 2x – 3 ≥ 0
(x – 3)(x + 1) ≥ 0
Por lo tanto, x < -1 o x > 3
Pregunta 23. Si los términos p th , q th y r th de a AP y GP son a, b y c respectivamente, demuestre que a b-c b c-a c a-b = 1.
Solución:
Consideremos que el AP sea A, A + D, A + 2D, …. y GP sea x, xR, xR 2 ,
Después
a = A + (p – 1)D, B = A + (q – 1)D, c = A + (r – 1)D
a – b = (p – q)D, b – c = (q – r)D, c – a = (r – p)D
También a = XR p-1 , b = xR q-1 , c = xR r-1
Por lo tanto, a b-c .b c-a .c a-b = (xR p-1 ) (qr)D .(xR q-1 ) (rp)D .(xR r-1 ) (pq)D
= x (q-r+r-p+pq)D .R [(p-1)(qr)+(q-1)(rp)+(r-1)(pq)]D
= x 0 .R 0
= 1,1
= 1
Publicación traducida automáticamente
Artículo escrito por mallikagupta90 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
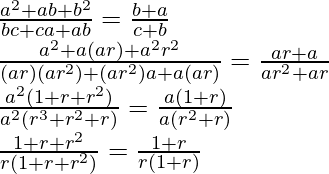
![Rendered by QuickLaTeX.com \frac{a_q}{a_p}=\frac{a_r}{a_q}\\ =\frac{a_q-a_r}{a_p-a_q}\ \ \ -(Using \ ratio\ property)\\ =\frac{[a+(q-1)d]-[a+(r-1)d]}{[a+(p-1)d]-[a+(q-1)d]}\\ =\frac{(q-r)d}{(p-q)d}\\ R=\frac{q-r}{p-q}\ \ \ \ -(1)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6830ce404e56bed6e979ad0f3d0b86a2_l3.png)
![Rendered by QuickLaTeX.com R=\frac{a_r}{a_q}=\frac{a_s}{a_r}\\ =\frac{a_r-a_s}{a_q-a_r}\ \ \ \ -(Using \ ratio\ property)\\ =\frac{[a+(r-1)d]-[a+(s-1)d]}{[a+(q-1)d]-[a+(r-1)d]}\\ =\frac{(r-s)d}{(q-r)d}\\ R=\frac{r-s}{q-r}\ \ \ \ \ -(2)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0e3f796672177391a1b0f90c3254b315_l3.png)
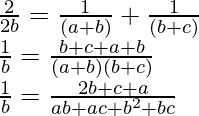
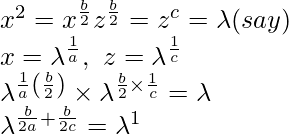
![Rendered by QuickLaTeX.com c^2=bd=2b\times\frac{d}{2}\\ ⇒ c^2=(a+c)\times\frac{ce}{c+e}\\ ⇒ c^2=\frac{(a+c)ce}{c+e}\ \ \ \ \ \left[\because\frac{2}{d}=\frac{e+c}{ce}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2676f75793b569623f1846ef696c41f2_l3.png)