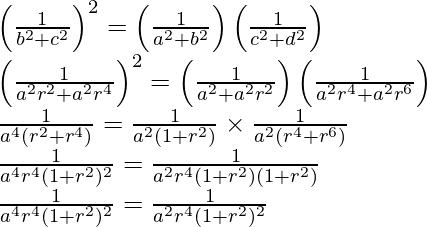Clase 11 Soluciones RD Sharma – Capítulo 20 Progresiones geométricas – Ejercicio 20.5 | Serie 1

Pregunta 1. Si a, b, c están en GP, ​​prueba que log a, log b, log c están en AP

Solución:

Dado: a, b y c están en GP

Usando la propiedad de la media geométrica, obtenemos

b ² = ca 

(b ² ) ^norte = (ac) ^norte

segundo ² norte = un ^norte do ^norte

Ahora, use log en ambos lados, obtenemos,

log b ²ⁿ = log (a ⁿ c ⁿ )

log (b ⁿ ) ² = log a ⁿ + log c ⁿ

2 log b ⁿ = log a ⁿ + log c ⁿ

Por lo tanto, probado log a ⁿ , log b ⁿ , log c ⁿ están en AP

Pregunta 2. Si a, b, c están en GP, ​​prueba que 1/log _a m, 1/log _b m, 1/log _c m están en AP

Solución:

Dado: a, b y c están en GP

Usando la propiedad de la media geométrica

b ² = ca 

Al aplicar log en ambos lados con base m, obtenemos

log _m b ² = log _m ca

Usando la propiedad de registro

log _m b ² = log _m a + log _m c 

2log _m b = log _m a + log _m c

2/log _b m = 1/log _a m + 1/log _c m

Por lo tanto, se demostró que 1/log _a m, 1/log _b m, 1/log _cm están en AP

Pregunta 3. Encuentre k tal que k + 9, k – 6 y 4 formen tres términos consecutivos de un GP

Solución:

Consideremos  

a = k + 9

segundo = k – 6 

c = 4

COMO sabemos que a, b y c están en GP, ​​entonces

Usando la propiedad de la media geométrica, obtenemos

b ² = ca 

(k – 6) ² = 4 (k + 9)

k2 – 12k ⁺ 36 = 4k + 36

k ² – 16k = 0

k = 0 o k = 16

Pregunta 4. Tres números están en AP, y su suma es 15. Si se les suma 1, 3, 9 respectivamente, forman un GP encuentra los números.

Solución:

Consideremos el primer término de un AP = a  

Diferencia común = d

un ₁ + un ₂ + un ₃ = 15

Aquí, los tres números son: a, a + d y a + 2d

Asi que,

a + a + d + a + 2d = 15

3a + 3d = 15 o a + d = 5

d = 5 – a -(1)

a + 1, a + d + 3 y a + 2d + 9

Están en GP, ​​es decir:

(a + re + 3)/(a + 1) = (a + 2d + 9)/(a + re + 3)

(a + d + 3) ² = (a + 2d + 9)(a + 1)

un ² + re ² + 9 + 2ad + 6d + 6a = un ² + un + 2da + 2d + 9a + 9

(5 – a) ² – 4a + 4(5 – a) = 0

25 + un ² – 10a – 4a + 20 – 4a = 0

un ² – 18a + 45 = 0

un ² – 15a – 3a + 45 = 0

a(a-15)-3(a-15) = 0

a = 3 o a = 15

d = 5 – un

d = 5 – 3 o d = 5 – 15

d = 2 o – 10

Después,

Para a = 3 y d = 2, AP es 3, 5, 7

Para a = 15 y d = -10, AP es 15, 5, -5

Por lo tanto, los números son 3, 5, 7 o 15, 5, – 5

Pregunta 5. La suma de tres números que son términos consecutivos de un AP es 21. Si al segundo número se le resta 1 y al tercero se le aumenta 1, obtenemos tres términos consecutivos de un GP Halla los números.

Solución:

Consideremos que el primer término de un AP sea = a

Diferencia común = d

un ₁ + un ₂ + un ₃ = 21

Aquí, los tres números son: a, a + d y a + 2d

Asi que,

3a + 3d = 21 o

a + re = 7.

d = 7 – a -(1)

a, a + d – 1, y a + 2d + 1

Ahora están en GP, ​​es decir:

(a + d – 1)/a = (a + 2d + 1)/(a + d – 1)

(a + d – 1) ² = a(a + 2d + 1)

a ² + d ² + 1 + 2ad – 2d – 2a = a ² + a + 2da

(7 – a) ² – 3a + 1 – 2(7 – a) = 0

49 + un ² – 14a – 3a + 1 – 14 + 2a = 0

un ² – 15a + 36 = 0

un ² – 12a – 3a + 36 = 0

a(a-12)-3(a-12) = 0

a = 3 o a = 12

d = 7 – un

d = 7 – 3 o d = 7 – 12

d = 4 o – 5

Después,

Para a = 3 y d = 4, AP es 3, 7, 11

Para a = 12 y d = -5, AP es 12, 7, 2

Por lo tanto, los números son 3, 7, 11 o 12, 7, 2

Pregunta 6. La suma de tres números a, b, c en AP es 18. Si cada uno de ayb aumenta en 4 y c aumenta en 36, los nuevos números forman un GP Halla a, b, c.

Solución:

Consideremos el primer término de un AP = a 

Diferencia común = d

b = a + d; c = a + 2d.

Dado:

a + b + c = 18

3a + 3d = 18 o a + d = 6.

d = 6 – a -(1)

a + 4, a + d + 4 y a + 2d + 36

Ahora están en GP, ​​es decir:

(a + re + 4)/(a + 4) = (a + 2d + 36)/(a + re + 4)

(a + d + 4) ² = (a + 2d + 36)(a + 4)

un ² + re ² + 16 + 8a + 2ad + 8d = un ² + 4a + 2da + 36a + 144 + 8d

d2-32a ^– 128

(6 – a) ² – 32a – 128 = 0

36 + un ² – 12a – 32a – 128 = 0

un ² – 44a – 92 = 0

a ² – 46a + 2a – 92 = 0

a(a-46) + 2(a-46) = 0

a = – 2 o a = 46

d = 6 –a

d = 6 – (– 2) o d = 6 – 46

d = 8 o – 40

Después,

Para a = -2 y d = 8, AP es -2, 6, 14

Para a = 46 y d = -40, AP es 46, 6, -34

Por lo tanto, los números son – 2, 6, 14 o 46, 6, – 34

Pregunta 7. La suma de tres números en GP es 56. Si restamos 1, 7, 21 de estos números en ese orden, obtenemos un AP Encuentra los números.

Solución:

Consideremos los tres números = a, ar, ar ²

a + ar + ar ² = 56 -(1)

Ahora, resta 1, 7, 21 de los números, obtenemos,

(a – 1), (ar – 7), (ar ² – 21)

Los números anteriores están en AP.

Si tres números están en AP, 

Entonces, de acuerdo con la media aritmética, podemos escribir como 2b = a + c

2 (ar – 7) = a – 1 + ar ² – 21

= (ar ² + a) – 22

2ar – 14 = (56 – ar) – 22

2ar – 14 = 34 – ar

3ar = 48

ar = 48/3

ar = 16

a = 16/r -(2)

Ahora, sustituimos el valor de a en la ecuación (1) obtenemos,

(16 + 16r + 16r ² )/r = 56

16 + 16r + 16r ² = 56r

16r ² – 40r + 16 = 0

2r ² – 5r + 2 = 0

2r ² – 4r – r + 2 = 0

2r(r-2)-1(r-2) = 0

(r-2) (2r-1) = 0

r = 2 o 1/2

Sustituyendo el valor de r en la ecuación (2) obtenemos,

a = 16/r

= 16/2 o 16/(1/2)

= 8 o 32

Por lo tanto, los tres números son (a, ar, ar ² ) es (8, 16, 32)

Pregunta 8. Si a, b, c están en GP, ​​demuestre que:

(i) a(b2 + c ² ) = c(a ² + b ² )

(ii) a ² b ² c ² [1/a ³ + 1/b ³ + 1/c ³ ] = a ³ + b ³ + c ³

(iii) (a+b+c) ² / (a ^​​2 + b ² + c ² ) = (a+b+c) / (a-b+c)

(iv) 1/(a ² – b ² ) + 1/b ² = 1/(b ² – c ² )

(v) (a + 2b + 2c) (a – 2b + 2c) = a ² + 4c ²

Solución:

(i) Dado: a, b, c están en GP.

Usando la propiedad de la media geométrica,

b ² = ca

Sea LHS: a(b ² + c ² )

Ahora, al sustituir b ² = ac, obtenemos

a(ac + c ² )

a ² c + ac ²

c(a ² + ac)

Al sustituir ac = b ² obtenemos,

c(a ² + b ² ) = lado derecho

LHS = RHS

Por lo tanto, probado.

(ii) Dado: a, b, c están en GP.

Usando la propiedad de la media geométrica,

b ² = ca

Sea LHS: a ² b ² c ² [1/a ³ + 1/b ³ + 1/c ³ ]

a ² b ² c ² /a ³ + a ² b ² c ² /b ³ + a ² b ² c ² /c ³

b ² c ² /a + a ² c ² /b + a ² b ² /c

(ac)c ² /a + (b ² ) ² /b + a ² (ac)/c -( b ² = ac)

ac ³ /a + b ⁴ /b + a ³ c/c

do ³ + segundo ³ + un ³ = lado derecho

LHS = RHS

Por lo tanto, probado.

(iii) Dado: a, b, c están en GP.

 Usando la propiedad de la media geométrica,

b ² = ca

Sea LHS: (a + b + c) ² / (a ^​​2 + b ² + c ² )

(a + b + c) ² / (a ^​​2 + b ² + c ² ) = (a + b + c) ² /(a ² – b ² + c ² + 2b ² )

= (a + b + c) ² / (a ^​​2 – b ² + c ² + 2ac) -(b ² = ac)

= (a + b + c) ² / (a ​​+ b + c)(a – b + c) -((a + b + c)(a – b + c) = a ² – b ² + c ² + 2ac)

= (a + b + c) / (a ​​– b + c)

= lado derecho

LHS = RHS

Por lo tanto, probado.

(iv) Dado: a, b, c están en GP.

Usando la propiedad de la media geométrica,

b ² = ca

Sea LHS: 1/(a ² – b ² ) + 1/b ²

Al tomar LCM, obtenemos

1/(a ² – b ² ) + 1/b ² = (b ² + a ² – b ² )/(a ² – b ² )b ²

= un ² / (un ^{2 segundo} 2 ^– segundo ⁴ )

= un ² / (un ^{2 segundo 2} – ( b ² ) ² )

= a ² / (a ^​​2 b ² – (ac) ² ) -(b ² = ac)

= un ² / (un ^{2 segundo 2} – un ² c ² )

= un ² / un ² (b ² – c ² )

= 1/ (b ² – c ² )

= lado derecho

LHS = RHS

Por lo tanto, probado.

(v) Dado: a, b, c están en GP.

Usando la propiedad de la media geométrica,

b ² = ca

Sea LHS: (a + 2b + 2c) (a – 2b + 2c)

Ahora, al expandir, obtenemos

(a + 2b + 2c) (a – 2b + 2c) = a ² – 2ab + 2ac + 2ab – 4b ² + 4bc + 2ac – 4bc + 4c ²

= a ² + 4ac – 4b ² + 4c ²

= a ² + 4ac – 4(ac) + 4c ²         -(b ² = ac)

= un ² + 4c ²

= lado derecho

LHS = RHS

Por lo tanto, probado.

Pregunta 9. Si a, b, c, d están en GP, ​​pruebe que:

(i) (ab – cd) / (b ² – c ² ) = (a + c) / b

(ii) (a + b + c + d) ² = (a + b) ² + 2 (b + c) ² + (c + d) ²

(iii) (b + c) (b + d) = (c + a) (c + d)

Solución:

(i) Dado: a, b, c están en GP.

Usando la propiedad de la media geométrica,

b ² = ca

bc = anuncio

c ² = bd

Sea LHS: (ab – cd) / (b ² – c ² )

(ab – cd) / (b ² – c ² ) = (ab – cd) / (ac – bd)

= (ab – cd)b / (ac – bd)b

= (ab ² – bcd) / (ac – bd)b

= [a(ac) – c(c ² )] / (ac – bd)b

= (a ² c – c ³ ) / (ac – bd)b

= [c(a ² – c ² )] / (ac – bd)b

= [(a + c) (ac – c ² )] / (ac – bd)b

= [(a + c) (ac – bd)] / (ac – bd)b

= (a + c) / b

= lado derecho

LHS = RHS

Por lo tanto, probado.

(ii) Dado: a, b, c están en GP.

Usando la propiedad de la media geométrica,

b ² = ca

bc = anuncio

c ² = bd

Sea RHS: (a + b) ² + 2 (b + c) ² + (c + d) ²

Ahora, al expandir, obtenemos

(a + b) ² + 2 (b + c) ² + (c + d) ² = (a + b) ² + 2 (a + b) (c + d) + (c + d) ²

= a ² + b ² + 2ab + 2(c ² + b ² + 2cb) + c ² + d ² + 2cd

= un ² + ^{segundo 2} + c ² + re ² + 2ab + 2 (c ² + ^{segundo 2} + 2cb) + 2cd

= a ² + b ² + c ² + d ² + 2(ab + bd + ac + cb + cd) -(c ² = bd, b ² = ac)

(a + b + c) ² + re ² + 2d (a + b + c) = {(a + b + c) + d} ²

RHS = LHS

Por lo tanto, probado.

(iii) Dado: a, b, c están en GP.

Usando la propiedad de la media geométrica,

b ² = ca

bc = anuncio

c ² = bd

Sea LHS: (b + c) (b + d)

Ahora, al expandir, obtenemos

(b + c) (b + d) = b ² + bd + cb + cd

= ac + c ² + anuncio + cd

= c (a + c) + d (a + c)

= (a + c) (c + d)

= lado derecho

LHS = RHS

Por lo tanto, probado.

Pregunta 10. Si a, b, c están en GP, ​​demuestre que los siguientes también están en GP:

(i) a ² , b ² , c ²

(ii) a ³ , b ³ , c ³

(iii) a ² + b ² , ab + bc, b ² + c ²

Solución:

(i) Dado: a, b, c están en GP.

Usando la propiedad de la media geométrica,

b ² = ca

Al elevar al cuadrado ambos lados obtenemos,

(b ² ) ² = (ac) ²

(b ² ) ² = un ² c ²

Por lo tanto, se demostró que a ² , b ² , c ² están en GP

(ii) Dado: a, b, c están en GP.

Usando la propiedad de la media geométrica,

b ² = ca

Al elevar al cuadrado ambos lados, obtenemos

(b ² ) ³ = (ac) ³

(b ² ) ³ = un ³ c ³

(b ³ ) ² = un ³ c ³

Por lo tanto, se demostró que a ³ , b ³ , c ³ están en GP

(iii) Dado: a, b, c están en GP.

Usando la propiedad de la media geométrica,

b ² = ca

a ² + b ² , ab + bc, b ² + c ² o (ab + bc) ² = (a ² + b ² ) (b ² + c ² ) 

Sea LHS: (ab + bc) ²

Ahora, al expandir, obtenemos

(ab + bc) ² = un ^{2 segundo 2} + 2ab ² c + ^{segundo 2} c ²

= un ^{2 segundo 2} + 2b 2 ⁽ segundo ² ) + ^{segundo 2} c ²            -(ac = ^{segundo 2)}

= un ^{2 segundo 2} + 2b 4 ⁺ segundo ² do ²

= un ² segundo ² + segundo ⁴ + un ² do ² + ^{segundo 2} do ²         -( ^{segundo 2} = ac)

= segundo 2 ( ^{segundo 2} + un ² ) + c ² (un ² + ^{segundo 2} )

= (a ² + b ² )(b ² + c ² )

= lado derecho

LHS = RHS

Por lo tanto, a ² + b ² , ab + bc, b ² + c ² están en GP.

Pregunta 11. Si a, b, c, d están en GP probar que;

(i) (a ² + b ² ), (b ² + c ² ), (c ² + d ² ) están en GP

(ii) (a ² – b ² ), (b ² – c ² ), (c ² – d ² ) están en GP

(iii) 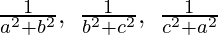  están en GP

(iv) (a ² + b ² + c ² ), (ab + bc + cd), (b ² + c ² + d ² ) están en GP

Solución:

(i) Dado: a, b, c, d están en GP

Entonces, a, b = ar, c = ar ² , d = ar ³

Ahora,

( ^{segundo 2} + c ² ) ² = (un ² + ^{segundo 2} )(c ² + re ² )

(un ² r ² + un ² r ⁴ ) ² = (un ² + un ² r ² )(un ² r ⁴ + un ² r ⁶ )

un ⁴ (r ² + r ⁴ ) = un ² (1 + r ² )un ² r ⁴ (1 + r ² )

un ⁴ r ⁴ (1 + r ² ) ² = un ⁴ r ⁴ (1 + r ² ) ²

LHS = RHS

⇒ ( ^{segundo 2} + c ² ) ² = (un ² + ^{segundo 2} )(c ² + re ² )

Por lo tanto, demostrado (a ² + b ² ), (b ² + c ² ), (c ² + d ² ) están en GP

(ii)  Dado: a, b, c, d están en GP

Entonces, a, b = ar, c = ar ² , d = ar ³

Ahora,

( ^{segundo 2} – c ² ) ² = (un ² – ^{segundo 2} )(c ² – re ² )

(un ² r ² – un ² r ⁴ ) = (un ² – un ² r ² )(un ² r ⁴ – un ² r ⁶ )

un ⁴ (r ² – r ⁴ ) ² = un ² (1 – r ² ) un ² r ⁴ (1 – r ² )

un ⁴ r ⁴ (1 – r ² ) ² = un ⁴ r ⁴ (1 – r ² ) ²

LHS = RHS

⇒ ( ^{segundo 2} – c ² ) ² = (un ² – ^{segundo 2} )(c ² – re ² )

Por lo tanto, demostrado (a ² – b ² ), (b ² – c ² ), (c ² – d ² ) están en GP

(iii) Dado: a, b, c, d están en GP

Entonces, a, b = ar, c = ar ² , d = ar ³

Ahora,

LHS = RHS

 

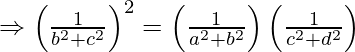
Por lo tanto, probado   están en GP

(iv) Dado: a, b, c, d están en GP

Entonces, a, b = ar, c = ar ² , d = ar ³

Ahora,

(ab + bc + cd) ² = (a ² + b ² + c ² )(b ² + c ² + d ² )

(un ² r + un ² r ³ + un ² r ⁵ ) ² = (un ² + un ² r ² + un ² r ⁴ )(un ² r ² + un ² r ⁴ + un ² r ⁶ )

un ⁴ (r + r ³ + r ⁵ ) ² = un ² (1 + r ² + r ⁴ ) un ² r ² ( 1 + r ² + r ⁴ )

un ⁴ r ² (1 + r ² + r ⁴ ) ² = un ⁴ r ² (1 + r ² + r ⁴ ) ²

LHS = RHS

⇒ (ab + bc + cd) ² = (a ² + b ² + c ² )(b ² + c ² + d ² )

Por lo tanto, demostrado (a ² + b ² + c ² ), (ab + bc + cd), (b ² + c ² + d ² ) están en GP