Pregunta 1: Inserta 6 medias geométricas entre 27 y 1/81.
Solución:
Sean las seis medias geométricas A 1 , A 2 , A 3 , A 4 , A 5 , A 6 .
Ahora, estos 6 términos se suman entre 27 y 1/81.
Entonces el GP se convierte en 27, A 1 , A 2 , A 3 , A 4 , A 5 , A 6 ,1/81 con el primer término (a) = 27, el número de términos (n) = 8 y el octavo término (a 8 ) = 1/81.
Sabemos que el término n de un GP está dado por n = ar n-1 , donde r es la razón común.
=> un 8 = 1/81
=> 27(r) 8-1 = 1/81
=> r7 = 1 /(81×27)
=> r 7 = (1/3) 7
=> r = 1/3
Entonces, las medias geométricas son:
A 1 = ar = 27 (1/3) = 9
A 2 = ar 2 = 27(1/3) 2 = 3
A 3 = ar 3 = 27(1/3) 3 = 1
A 4 = ar 4 = 27(1/3) 4 = 1/3
A 5 = ar 5 = 27(1/3) 5 = 1/9
A 6 = ar 6 = 27(1/3) 6 = 1/27
Por tanto, las 6 medias geométricas entre 27 y 1/81 son 9, 3, 1, 1/3, 1/9, 1/27.
Pregunta 2. Inserta 5 medias geométricas entre 16 y 1/4.
Solución:
Sean las cinco medias geométricas A 1 , A 2 , A 3 , A 4 , A 5 .
Ahora, estos 5 términos se suman entre 16 y 1/4.
Entonces el GP se convierte en 16, A 1 , A 2 , A 3 , A 4 , A 5 ,1/4 con el primer término (a) = 16, el número de términos (n) = 7 y el séptimo término (a 7 ) = 1/4.
Sabemos que el término n de un GP está dado por n = ar n-1 , donde r es la razón común.
=> un 7 = 1/4
=> 16(r 7-1 ) = 1/4
=> r6 = 1/64
=> r 6 = (1/2) 6
=> r = 1/2
Entonces, las medias geométricas son:
UN 1 = ar = 16(1/2) = 8
A 2 = ar 2 = 16(1/2) 2 = 4
A 3 = ar 3 = 16(1/2) 3 = 2
A 4 = ar 4 = 16(1/2) 4 = 1
A 5 = ar 5 = 16(1/2) 5 = 1/2
Por tanto, las 5 medias geométricas entre 16 y 1/4 son 8, 4, 2, 1, 1/2.
Pregunta 3. Inserta 5 medias geométricas entre 32/9 y 81/2.
Solución:
Sean las cinco medias geométricas A 1 , A 2 , A 3 , A 4 , A 5 .
Ahora, estos 5 términos se suman entre el 32/9 y el 81/2.
Entonces el GP se convierte en 32/9, A 1 , A 2 , A 3 , A 4 , A 5 , 81/2 con el primer término (a) = 32/9, número de términos (n) = 7 y séptimo término ( a 7 ) = 81/2.
Sabemos que el término n de un GP está dado por n = ar n-1 , donde r es la razón común.
=> un 7 = 81/2
=> (32/9)(r 7-1 ) = 81/2
=> r6 = (81×9)/(2×32)
=> r 6 = (3/2) 6
=> r = 3/2
Entonces, las medias geométricas son:
A1 = ar = (32/9)×(3/2) = 16/3
A 2 = ar 2 = (32/9) × (3/2) 2 = 8
A 3 = ar 3 = (32/9) × (3/2) 3 = 12
A 4 = ar 4 = (32/9) × (3/2) 4 = 18
A 5 = ar 5 = (32/9) × (3/2) 5 = 27
Por tanto, las 5 medias geométricas entre 32/9 y 81/2 son 16/3, 8, 12, 18, 27.
Pregunta 4. Encuentra las medias geométricas de los siguientes pares de números:
(yo) 2 y 8
(ii) a 3 b y ab 3
(iii) -8 y -2
Solución:
Sabemos que la media geométrica entre dos números, a y b está dada por
.
(yo) 2 y 8
Aquí, a = 2 y b = 8
Entonces, GM =
=
= 4
(ii) a 3 b y ab 3
Aquí, a = a 3 b y b = ab 3
Entonces, GM =
=
= un 2 segundo 2
(iii) -8 y -2
Aquí, a = –8 y b = –2
GM =
=
= 4
Pregunta 5. Si a es el GM de 2 y 1/4 encuentra a.
Solución:
Sabemos que la media geométrica entre dos números, a y b está dada por
.
Según la pregunta,
un =
=
=
Por lo tanto, el valor de a es
.
Pregunta 6. Encuentra los dos números cuyo AM es 25 y GM es 20.
Solución:
Conocemos la media geométrica entre dos números, a y b está dada por
y la media aritmética entre dos números, a y b está dada por (a+b)/2.
Según la pregunta,
=>
= 20 ……. (1)
Y
=> (a+b)/2 = 25
=> a+b = 50
=> b = 50–a ……. (2)
De (1) y (2), obtenemos,
=>
= 20
Elevando al cuadrado ambos lados, obtenemos,
=> a(50 –a) = 400
=> un 2 – 50a + 400 = 0
=> un 2 – 40a–10a+400 = 0
=> a(a– 40) – 10(a– 40) = 0
=> (a-40) (a-10) = 0
=> a = 40 o a = 10
Poniendo esto en (2) obtenemos,
Cuando a = 40, entonces b = 10 y
Cuando a = 10, entonces b = 40.
Por lo tanto, los números son 10 y 40.
Pregunta 7. Construye una cuadrática en x tal que AM de sus raíces sea A y GM sea G.
Solución:
Supongamos que las raíces de la ecuación cuadrática son a y b.
Conocemos la media geométrica entre dos números, a y b está dada por
y la media aritmética entre dos números, a y b está dada por (a+b)/2.
Según la pregunta,
AM de raíces = (a+b)/2 = A
a + b = 2A ….. (1)
Y GM de raíces =
= G
ab = sol 2 … (2)
Ahora, sabemos que una ecuación cuadrática en x con raíces a y b está dada por,
x2 – (a+b)x + (ab) = 0
De (1) y (2), obtenemos,
x2 – 2Ax + G2 = 0
Por lo tanto, la ecuación cuadrática requerida es x 2 – 2Ax + G 2 = 0.
Pregunta 8. La suma de dos números es 6 veces su media geométrica. Demostrar que los números están en razón 
Solución:
Sean los dos números a y b. Sabemos que la media geométrica entre dos números, a y b está dada por
.
Según la pregunta,
=> a+b = 6
=>
=
Aplicando Componendo y Dividendo en ambos lados, obtenemos,
=>
=
=>
=
=>
=
Aplicando nuevamente Componendo y Dividendo en ambos lados, obtenemos,
=>
=
=>
=
=>
=
Elevando al cuadrado ambos lados, obtenemos
=>
=
=>
=
=>
=
Por lo tanto probado.
Pregunta 9. Si AM y GM de raíces de una ecuación cuadrática son 8 y 5 respectivamente, entonces obtenga la ecuación cuadrática.
Solución:
Supongamos que las raíces de la ecuación cuadrática son a y b.
Conocemos la media geométrica entre dos números, a y b está dada por
y la media aritmética entre dos números, a y b está dada por (a+b)/2.
Según la pregunta,
AM de raíces = (a+b)/2 = 8
a+b = 16 ….. (1)
Y GM de raíces =
= 5
ab = 25 .… (2)
Ahora, la ecuación cuadrática con raíces a y b está dada por,
x2 – (a+b)x + (ab) = 0
De (1) y (2), obtenemos,
x 2 – 16x + 25 = 0
Por lo tanto, la ecuación cuadrática requerida es x 2 – 16x + 25 = 0.
Pregunta 10. Si AM y GM de los dos números positivos a y b son 10 y 8 respectivamente. Encuentra los números.
Solución:
Conocemos la media geométrica entre dos números, a y b está dada por
y la media aritmética entre dos números, a y b está dada por (a+b)/2.
Según la pregunta,
=>
= 8 ……. (1)
Y,
=> (a+b)/2 = 10
=> a+b = 20
=> b = 20–a ……. (2)
De (1) y (2), obtenemos,
=>
= 8
Elevando al cuadrado ambos lados, obtenemos,
=> a(20–a) = 64
=> un 2 –20a+64 = 0
=> un 2 –16a–4a+64 = 0
=> a(a–16) – 4(a–16) = 0
=> (a–4) (a–16) = 0
=> a = 4 o a = 16
Poniendo a = 4 en (2), obtenemos b = 16. Y,
Poniendo a = 16 en (2), obtenemos b = 4.
Por lo tanto, los números son 4 y 16.
Pregunta 11. Demostrar que el producto de n medias geométricas entre dos cantidades es igual a la n-ésima potencia de la media geométrica de esas dos cantidades.
Solución:
Supongamos que tenemos un GP con primer término a, razón común r y número de términos n.
Tenemos que sumar estos n términos de GP entre dos cantidades tal que se mantenga el GP. Así que el número total de términos se convierte en (n+2).
Sabemos que el término n de un GP está dado por a n = ar n-1 .
Entonces, el último término del GP, es decir, (n+2) el término será, a n+2 = ar n+2-1 = ar n+1
Sabemos que la media geométrica entre dos números, a y b está dada por
.
El GM de a y ar n+1 será, G 1 =
=
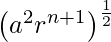
Por lo tanto, LHS = =
Ahora, RHS = Producto de n medias geométricas entre estas dos cantidades, G 2 = ar × ar 2 × . . . . × ar n
=
=
=
=
= LHS
Por lo tanto, Probado.
Pregunta 12: Si el AM de dos números positivos a y b (a>b) es el doble de su media geométrica. Demostrar que a:b = 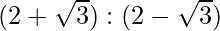
Solución:
Conocemos la media geométrica entre dos números, a y b está dada por
y la media aritmética entre dos números, a y b está dada por (a+b)/2.
Según la pregunta,
AM = 2 (GM)
=>
=
=>
=
Aplicando Componendo y Dividendo en ambos lados, obtenemos,
=>
=
=>
=
=>
=
Aplicando nuevamente Componendo y Dividendo en ambos lados, obtenemos,
=>
=
=>
=
=>
=
Elevando al cuadrado ambos lados, obtenemos
=>
=
=>
=
=>
=
=>
=
Por lo tanto, probado.
Pregunta 13. Si se insertan un AM, A y dos medias geométricas G 1 y G 2 entre dos números positivos cualesquiera, demuestre que 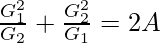
Solución:
Sean a y b los dos números positivos.
Ahora valor de un AM entre a y b, A = (a+b)/2.
Entonces, 2A = a+b. . . . (1)
Si sumamos dos medias geométricas entre ayb, el GP se convierte en a,G 1 ,G 2 ,b.
Ahora sabemos que b = ar 4-1 , donde r es la razón común.
=> r 3 =
=> r =
Entonces, G 1 = ar =
=
G 2 = ar 2 =
=
Ahora, LHS =
=
= ab 0 + a 0 b
= a+b
= 2A [De (1)]
= lado derecho
Por lo tanto, probado.
Publicación traducida automáticamente
Artículo escrito por gurjotloveparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
![Rendered by QuickLaTeX.com \left[\frac{\sqrt{2}+1}{\sqrt{2}-1}\right]^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e234eb96ade88cc98c5c248e525ba8a8_l3.png)
![Rendered by QuickLaTeX.com \left[\frac{\sqrt{3}+1}{\sqrt{3}-1}\right]^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9dba7f32fb739220c4c77329e056f99f_l3.png)
