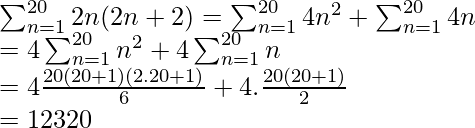Encuentra la suma de las siguientes series en n términos. (Pregunta 1-5)
Pregunta 1. 1 3 + 3 3 + 5 3 + 7 3 + ……
Solución:
Supongamos que T n es el enésimo término de la serie dada.
Ahora tenemos:
T norte = [1 + (n – 1) 2 ] 3
= (2n – 1) 3
= (2n) 3 – 3 (2n) 2 . 1 + 3.1 2 .2n – 1 3 [Ya que, (a – b) 3 = a 3 – 3a 2 b + 3ab 2 – b]
= 8n 3 – 12n 2 + 6n – 1
Además, supongamos que S n es la suma de n términos de la serie dada.
Simplificando la ecuación obtenemos
= 2n 2 (n + 1) 2 – n – 2n (n + 1) (2n + 1) + 3n (n + 1)
= norte (n + 1) [2n (n + 1) – 2 (2n + 1) + 3] – norte
= norte (n + 1) [2n 2 – 2n + 1] – norte
= norte [2n 3 – 2n 2 + norte + 2n 2 – 2n + 1 – 1]
= norte [2n 3 – n]
= norte 2 [2n 2 – 1]
Por lo tanto,
La suma de la serie es n 2 [2n 2 – 1].
Pregunta 2. 2 3 + 4 3 + 6 3 + 8 3 + ………
Solución:
Supongamos que T n es el enésimo término de la serie dada.
Ahora tenemos:
Tn = (2n ) 3
= 8n 3
Además, supongamos que S n es la suma de n términos de la serie dada.
Por lo tanto,
2
Pregunta 3. 1.2.5 + 2.3.6 + 3.4.7 + ……
Solución:
Supongamos que T n es el enésimo término de la serie dada.
Ahora tenemos:
T norte = norte ( n + 1) (n + 4)
= norte ( n2 + 5n + 4)
= n 3 + 5n 2 + 4n
Además, supongamos que S n es la suma de n términos de la serie dada.
Por lo tanto,
Pregunta 4. 1.2.4 + 2.3.7 + 3.4.10 + ….
Solución:
Supongamos que T n es el enésimo término de la serie dada.
Ahora tenemos:
T norte = norte ( n + 1) (3n + 1)
= n (3n 2 + 4n + 1)
= 3n 3 + 4n 2 + n
Además, supongamos que S n es la suma de n términos de la serie dada.
Por lo tanto,
Pregunta 5. 1 + (1 + 2) + (1 + 2 + 3) + (1 + 2 + 3 + 4) + …
Solución:
Supongamos que T n es el enésimo término de la serie dada.
Ahora tenemos:
T norte = n(n + 1)/2
= (n2 + n)/ 2
Además, supongamos que S n es la suma de n términos de la serie dada.
Por lo tanto,
Pregunta ××××
Solución:
Supongamos que T n es el enésimo término de la serie dada.
T n = (enésimo término de 1, 2, 3..) x (enésimo término de 2, 3, 4…)= [1 + (n + 1) x 1].[2 + (n + 1) x 1]
= [1 + n – 1].[2 + n – 1]
= n(n + 1)
= norte 2 + norte
Además, supongamos que S n es la suma de n términos de la serie dada.
Pregunta ×××
Solución:
Supongamos que T n es el enésimo término de la serie dada.
T n = (enésimo término de 3, 5, 7..) x (enésimo término de 1 2 , 2 2 , 3 2 …)
= [3 + (n – 1) x 2].[n 2 ]
= [2n + 1]. [n 2 ]
= 2n 3 + n 2
T norte = 2n 3 + norte 2
Además, supongamos que S n es la suma de n términos de la serie dada.
Por lo tanto,
La suma de la serie =
Pregunta
Solución:
T norte =
Además, supongamos que S n es la suma de n términos de la serie dada.
Suma de n términos =
Pregunta
Solución:
T norte =
Además, supongamos que S n es la suma de n términos de la serie dada.
Pregunta
Solución:
T norte =
Además, supongamos que S n es la suma de n términos de la serie dada.
Pregunta
Solución:
T norte = (
Además, supongamos que S n es la suma de n términos de la serie dada.
Pregunta 9. Encuentra el vigésimo término y la suma de 20 términos de la serie 2 × 4 + 4 × 6 + 6 × 8 +…..
Solución:
Supongamos que T n es el enésimo término de la serie dada.
El vigésimo término de la serie es:
La serie infinita es equivalente a,
2 × 4 + 4 × 6 + 6 × 8 + …. =
La suma de la serie hasta el término 20 es equivalente a
Publicación traducida automáticamente
Artículo escrito por yashchuahan y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
![Rendered by QuickLaTeX.com S_n = \sum_{k=1}^n T_k \\ = \sum_{k=1}^n [2k-1]^3 \\ = \sum_{k=1}^n [8k^3 - 1 - 6k(2k-1)] \\ = \sum_{k=1}^n [8k^3 - 1 - 12k^2 + 6k] \\ = 8 \sum_{k=1}^n k^3 - \sum_{k=1}^n 1 - 12 \sum_{k=1}^n k^2 + 6 \sum_{k=1}^n k \\ = \frac{8n^2(n+1)^2}{4} - n - \frac{12n(n+1)(2n+1)}{6} + \frac{6n(n+1)}{2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4b3f404061890d676387f430dba3ff0b_l3.png)
![Rendered by QuickLaTeX.com S_n = \sum_{k=1}^n 8k^3 \\ = 8 \sum_{k=1}^n k^3 \\ = 8[\frac{n(n+1)}{2}]^2 \\ = 8 * \frac{n^2(n+1)^2}{4} \\ = 2n^2(n+1)^2 \\ = 2{n(n+1)}^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9d182ae7c8f18172ae141707b3c0089c_l3.png)
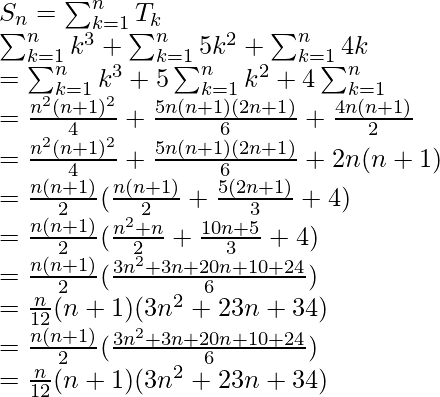
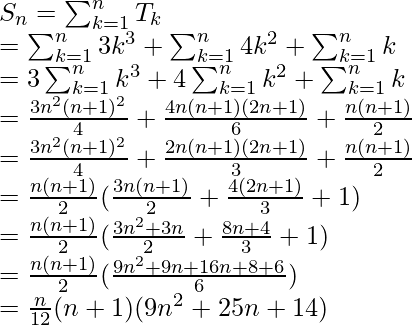
![Rendered by QuickLaTeX.com S_n = \sum_{k=1}^n T_k \\ = \sum_{k=1}^n (\frac{k^2+k}{2}) \\ = 1/2 \sum_{k=1}^n (k^2+k) \\ = 1/2 [\frac{n(n+1)(2n+1)}{6} + \frac{n(n+1)}{2} ] \\ = \frac{n(n+1)}{4}(\frac{2n+1}{3} + 1) \\ = \frac{n(n+1)}{4} (\frac{2n+4}{3}) \\ = \frac{n(n+1)(2n+4)}{12} \\ = \frac{n(n+1)(n+2)}{6}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-59256d777eca7d108eb458320e76be62_l3.png)
![Rendered by QuickLaTeX.com S_n = \sum_{k=1}^n T_n \\ = \sum_{k=1}^n (n^2 + n) \\ = \frac{n(n+1)(2n+1)}{6} + \frac{n(n+1)}{2} \\ = \frac{n(n+1)(2n+1)+3n(n+1)}{6} \\ = \frac{n(n+1)[2n+1+3]}{6} \\ = \frac{n(n+1)[2n+4]}{6} \\ = \frac{n(n+1) x 2 (n+2)}{6} \\ = \frac{n}{6} (n+1)(n+2)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-85fc5b50339656f765a9ed652458e88f_l3.png)
![Rendered by QuickLaTeX.com S_n = \sum_{k=1}^n T_n \\ = \sum_{k=1}^n (2n^3 + n^2) \\ = \sum_{k=1}^n 2n^3 + \sum_{k=1}^n n^2 \\ = 2 \sum_{k=1}^n n^3 + \sum_{k=1}^nn^2 \\ = 2[\frac{n(n+1)}{2}]^2 + [\frac{n(n+1)(2n+1)}{6}] \\ = \frac{2}{4}[n(n+1)]^2 + \frac{n(n+1)(2n+1)}{6} \\ = [\frac{n(n+1)}{2}]^2 + \frac{n(n+1)(2n+1)}{6} \\ = \frac{n(n+1)}{6}[3n(n+1)+(2n+1)] \\ = \frac{n(n+1)}{6}[3n^2+3n+2n+1] \\ \frac{n}{6}(n+1)(3n^2+5n+1)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cb6444b5dabe0172475f1ee0076e02db_l3.png)
![Rendered by QuickLaTeX.com S_n = \sum_{k=1}^{n}T_k \\ = 2 \sum_{k=1}^{n} 2k^3+ \sum_{k=1}^{n}3k^2 - \sum_{k=1}^{n} 1 \\ = 2[\frac{n(n+1)}{2}]^2 + 3[\frac{n(n+1)(2n+1)}{6}] -n \\ = \frac{2}{4}[n(n+1)]^2 + \frac{n(n+1)(2n+1) - n }{2} \\ = \frac{[n(n+1]^2+n(n+1)(2n+1)-n}{2} \\ = \frac{n}{2}[n(n+1)^2 + (n+1)(2n+1) - 2] \\ = \frac{n}{2} [n^3+n+2n^2+2n^2+3n-1] \\ = \frac{n}{2} [n^3+4n^2+4n-1]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-05eacf14c561329762511541be707d5a_l3.png)
![Rendered by QuickLaTeX.com S_n = \sum_{k=1}^{n}T_k \\ = \sum_{k=1}^{n}(k^3-3^k) \\ = \sum_{k=1}^{n} k^3 - \sum_{k=1}^{n} 3^k \\ = [\frac{n(n+1)}{2}]^2-(3^1+3^2+...+3^n) \\ = \frac{n^2(n+1)^2}{4}-3\frac{3^n-1}{3-1} \\ = \frac{n^2(n+1)^2}{4}-\frac{3}{2}(3^n-1)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7affa9d38d0325b9ca339c10ac5d5846_l3.png)
![Rendered by QuickLaTeX.com S_n = \sum_{k=1}^{n}T_k \\ = \sum_{k=1}^{n}(k^3+5k^2+4k) \\ = \sum_{k=1}^{n} k^3 + \sum_{k=1}^{n} 5k^2 + \sum_{k=1}^{n} 4k \\ = \sum_{k=1}^{n} k^3 + 5 \sum_{k=1}^{n} k^2 + 4 \sum_{k=1}^{n}k \\ = [\frac{n(n+1)}{2}]^2 + 5[\frac{n(n+10(2n+1)}{6}]+\frac{4n(n+1)}{2} \\ = \frac{1}{4}[n(n+1)]^2 + \frac{5n(n+1)(2n+1}{6}+2n(n+1) \\ = \frac{3[n(n+1)]^2+10n(n+1)(2n+1)+24n(n+1)}{12} \\ = \frac{n(n+1)}{12}[3n(n+1)+10(2n+1)+24] \\ = \frac{n(n+1)}{12}[3n^2+23n+34]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e0422fa33ec900ae68b7cfa1e7f50b85_l3.png)
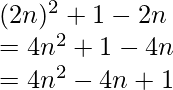
![Rendered by QuickLaTeX.com S_n = \sum_{k=1}^{n}T_k \\ = \sum_{k=1}^{n}4k +\sum_{k=1}^{n}1 \\ = \sum_{k=1}^{n}k^2 -4\sum_{k=1}^{n}k + \sum_{k=1}^{n}1 \\ = 4[\frac{n(n+1)(2n+1)}{6}]-4\frac{n(n+1)}{2}+n \\ = 2/3n(n+1)(2n+1)-2n(n+1)+n \\ = \frac{2}{3}n(n+1)(2n+1)-2n^2-2n+n \\ = \frac{2n}{3}(n+1)(2n+1) - n(2n+1) \\ = \frac{n}{3} (2n+1)[2(n+1)-3] \\ = \frac{n}{3}(2n+1)(2n+2-3) \\ = \frac{n}{3}(2n+1)(2n-1)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-43593d44f7b3dc8c640087fd228dc708_l3.png)