Clase 11 RD Sharma Solutions – Capítulo 21 Algunas series especiales – Ejercicio 21.2

Suma la siguiente serie en n términos:

Pregunta 1. 3 + 5 + 9 + 15 + 23 + . . . . n términos

Solución:

Nos dan la serie: 3 + 5 + 9 + 15 + 23 + . . . . n términos.

Tomemos S como la suma de esta serie. Por lo tanto,

S = 3 + 5 + 9 + 15 + 23 + . . . . + un _norte–1 + un _norte . . . .(1)

S = 3 + 5 + 9 + 15 + 23 + . . . . + un _norte–2 + un _norte–1 + un _norte . . . .(2)

Al restar (2) de (1), obtenemos

=> S – S = [3 + (5 + 9 + 15 + 23 + . . . . + un _n–1 + un _n )] – [(3 + 5 + 9 + 15 + 23 + . . . . + un _n–2 + un _n–1 ) + un _n ]

=> 0 = 3 + [(5 – 3) + (9 – 5) + (15 – 9) + . . . . + (un _norte – un _norte–1 )] – un _norte

=> un _norte = 3 + [2 + 4 + 6 + . . . . (n–1) términos]

Como la serie 2+ 4 + 6 + . . . . (n–1) términos es un AP, con el primer término (a) = 2 y la diferencia común (d) = 4–2 = 2. Entonces, obtenemos,

=> un norte = 3 + ( _n –1) [2(2)+(n–2)2]/2

= 3+ (n–1) [4+2n–4]/2

= 3 + n(n–1)

= norte ² – norte + 3

Ahora tenemos que sumar nuestro ^enésimo término para encontrar la suma (S _n ) de esta serie.

$S_n = \sum_{k=1}^{n} a_k = \sum_{k=1}^{n} k^2 - \sum_{k=1}^{n} k + \sum_{k=1}^{n} 3$

= $\frac{n(n+1)(2n+1)}{6}-\frac{n(n+1)}{2}+3n$

= $n\left[\frac{(n+1)(2n+1)-3(n+1)+18}{6}\right]$

= $\frac{n}{6}\left[2n^2+n+2n+1-3n-3+18\right]$

= $\frac{n}{6}\left[2n^2+16\right]$

= $\frac{n(n^2+8)}{3}$

Por tanto, la suma de la serie dada hasta n términos es $\frac{n(n^2+8)}{3}$ .

Pregunta 2. 2 + 5 + 10 + 17 + 26 + . . . . n términos

Solución:

Nos dan la serie: 2 + 5 + 10 + 17 + 26 + . . . . n términos.

Tomemos S como la suma de esta serie. Por lo tanto,

S = 2 + 5 + 10 + 17 + 26 + . . . . + un _norte–1 + un _norte . . . .(1)

S = 2 + 5 + 10 + 17 + 26 + . . . . + un _norte–2 + un _norte–1 + un _norte . . . .(2)

Al restar (2) de (1), obtenemos

=> S – S = [2 + (5 + 10 + 17 + 26 + . . . . + un _n–1 + un _n )] – [(2 + 5 + 10 + 17 + 26 + . . . . + un _n–2 + un _n–1 ) + un _n ]

=> 0 = 2 + [(5 – 2) + (10 – 5) + (17 – 10) + . . . . + (un _norte – un _norte–1 )] – un _norte

=> un _norte = 2 + [3 + 5 + 7 + . . . . (n–1) términos]

Como la serie 3 + 5 + 7 + . . . . (n–1) términos es un AP, con el primer término (a) = 3 y la diferencia común (d) = 5–3 = 2. Entonces, obtenemos,

=> un norte = 2 + ( _n –1) [2(3)+(n–2)2]/2

= 2+ (n–1) [6+2n–4]/2

= 2 + (n–1)(n+1)

= norte ² – 1 + 2

= norte ² + 1

Ahora tenemos que sumar nuestro ^enésimo término para encontrar la suma (S _n ) de esta serie.

$S_n = \sum_{k=1}^{n} a_k = \sum_{k=1}^{n} k^2 + \sum_{k=1}^{n} 1$

= $\frac{n(n+1)(2n+1)}{6}+n$

= $\frac{n(n+1)(2n+1)+6n}{6}$

= $\frac{n(2n^2+3n+7)}{6}$

Por tanto, la suma de la serie dada hasta n términos es $\frac{n(2n^2+3n+7)}{6}$ .

Pregunta 3. 1 + 3 + 7 + 13 + 21 + 31 + . . . . n términos

Solución:

Nos dan la serie: 1 + 3 + 7 + 13 + 21 + 31 + . . . . n términos.

Tomemos S como la suma de esta serie. Por lo tanto,

S = 1 + 3 + 7 + 13 + 21 + 31 + . . . . + un _norte–1 + un _norte . . . .(1)

S = 1 + 3 + 7 + 13 + 21 + 31 + . . . . + un _norte–2 + un _norte–1 + un _norte . . . .(2)

Al restar (2) de (1), obtenemos

=> S – S = [1 + (3 + 7 + 13 + 21 + 31 + . . . . + un _n–1 + un)] – [(1 + 3 + 7 + 13 + 21 + 31 + . . . . + un _n–2 + un _n–1 ) + un _n ]

=> 0 = 1 + [(3 – 1) + (7 – 3) + (13 – 7) + . . . . + (un _norte – un _norte–1 )] – un _norte

=> un _norte = 1 + [2 + 4 + 6 + . . . . (n–1) términos]

Como la serie 2 + 4 + 6 + . . . . (n–1) términos es un AP, con el primer término (a) = 2 y la diferencia común (d) = 4–2 = 2. Entonces, obtenemos,

=> un norte = 1 + ( _n –1) [2(2)+(n–2)2]/2

= 1+ (n–1) [4+2n–4]/2

= 1 + n(n–1)

= n2 – n ⁺ 1

Ahora tenemos que sumar nuestro ^enésimo término para encontrar la suma (S _n ) de esta serie.

$S_n = \sum_{k=1}^{n} a_k = \sum_{k=1}^{n} k^2 - \sum_{k=1}^{n} k + \sum_{k=1} ^{n}1$

= $\frac{n(n+1)(2n+1)}{6}-\frac{n(n+1)}{2}+n$

= $\frac{n(n+1)(2n+1)-3n(n+1)+6n}{6}$

= $\frac{n(2n^2+n+2n+1-3n-3+6)}{6}$

= $\frac{n(2n^2+4)}{6}$

= $\frac{n(n^2+2)}{3}$

Por tanto, la suma de la serie dada hasta n términos es $\frac{n(n^2+2)}{3}$ .

Pregunta 4. 3 + 7 + 14 + 24 + 37 + . . . . n términos

Solución:

Nos dan la serie: 3 + 7 + 14 + 24 + 37 + . . . . n términos.

Tomemos S como la suma de esta serie. Por lo tanto,

S = 3 + 7 + 14 + 24 + 37 + . . . . + un _norte–1 + un _norte . . . .(1)

S = 3 + 7 + 14 + 24 + 37 + . . . . + un _norte–2 + un _norte–1 + un _norte . . . .(2)

Al restar (2) de (1), obtenemos

=> S – S = [3 + (7 + 14 + 24 + 37 + . . . . + un _n–1 + un _n )] – [(3 + 7 + 14 + 24 + 37 + . . . . + un _n–2 + un _n–1 ) + un _n ]

=> 0 = 3 + [(7 – 3) + (14 – 7) + (24 – 14) + . . . . + (un _norte – un _norte–1 )] – un _norte

=> un _norte = 3 + [4 + 7 + 10 + . . . . (n–1) términos]

Como la serie 4 + 7 + 10 + . . . . (n–1) términos es un AP, con el primer término (a) = 4 y la diferencia común (d) = 7–4 = 3. Entonces, obtenemos,

=> un norte = 3 + ( _n –1) [2(4)+(n–2)3]/2

= 3+ (n–1) [8+3n–6]/2

= 3 + (n–1)(3n+2)/2

= $\frac{6+(n-1)(3n+2)}{2}$

= $\frac{6+3n^2-n-2}{2}$

= $\frac{3n^2-n+4}{2}$

Ahora tenemos que sumar nuestro ^enésimo término para encontrar la suma (S _n ) de esta serie.

$S_n = \sum_{k=1}^{n} a_k = \frac{1}{2}\left[\sum_{k=1}^{n} 3k^2 - \sum_{k=1}^{ n} k + \sum_{k=1}^{n} 4\right]$

= $\frac{3}{2}\sum_{k=1}^{n} k^2 - \frac{1}{2}\sum_{k=1}^{n} k + \sum_{k=1 }^{n} 2$

= $\frac{3}{2}[\frac{n(n+1)(2n+1)}{6}]-\frac{1}{2}[\frac{n(n+1)}{2 }]+2n$

= $\frac{n(n+1)(2n+1)-n(n+1)+8n}{4}$

= $\frac{n(2n^2+2n+8)}{4}$

= $\frac{n(n^2+n+4)}{2}$

Por tanto, la suma de la serie dada hasta n términos es $\frac{n(n^2+n+4)}{2}$ .

Pregunta 5. 1 + 3 + 6 + 10 + 15 + . . . . n términos

Solución:

Nos dan la serie: 1 + 3 + 6 + 10 + 15 + . . . . n términos.

Tomemos S como la suma de esta serie. Por lo tanto,

S = 1 + 3 + 6 + 10 + 15 + . . . . + un _norte–1 + un _norte . . . .(1)

S = 1 + 3 + 6 + 10 + 15 + . . . . + un _norte–2 + un _norte–1 + un _norte . . . .(2)

Al restar (2) de (1), obtenemos

=> S – S = [1 + (3 + 6 + 10 + 15 + . . . . + un _n–1 + un _n )] – [(1 + 3 + 6 + 10 + 15 + . . . . + un _n–2 + un _n–1 ) + un _n ]

=> 0 = 1 + [(3 – 1) + (6 – 3) + (10 – 6) + . . . . + (un _norte – un _norte–1 )] – un _norte

=> un _norte = 1 + [2 + 3 + 4 + . . . . (n–1) términos]

Como la serie 2 + 3 + 4 + . . . . (n–1) términos es un AP, con el primer término (a) = 2 y la diferencia común (d) = 3–2 = 1. Entonces, obtenemos,

=> un norte = 1 + ( _n –1) [2(2)+(n–2)1]/2

= 1+ (n–1) [4+n–2]/2

= 1 + (n–1)(n+2)/2

= $\frac{2+(n-1)(n+2)}{2}$

= $\frac{2+n^2+2n-n-2}{2}$

= $\frac{n^2+n}{2}$

Ahora tenemos que sumar nuestro ^enésimo término para encontrar la suma (S _n ) de esta serie.

$S_n = \sum_{k=1}^{n} a_k = \frac{1}{2}\left[\sum_{k=1}^{n} k^2 + \sum_{k=1}^{n} k\right]$

= $\frac{1}{2}\sum_{k=1}^{n} k^2 + \frac{1}{2}\sum_{k=1}^{n} k$

= $\frac{1}{2}\left[\frac{n(n+1)(2n+1)}{6}\right] + \frac{1}{2}\left[\frac{n(n+1)}{2}\right]$

= $\frac{n(n+1)}{2}\left[\frac{2n+1}{6}+\frac{1}{2}\right]$

= $\frac{n(n+1)(2n+4)}{12}$

= $\frac{n(n+1)(n+2)}{6}$

Por tanto, la suma de la serie dada hasta n términos es $\frac{n(n+1)(n+2)}{6}$ .

Pregunta 6. 1 + 4 + 13 + 40 + 121 + . . . . n términos

Solución:

Nos dan la serie: 1 + 4 + 13 + 40 + 121 + . . . . n términos.

Tomemos S como la suma de esta serie. Por lo tanto,

S = 1 + 4 + 13 + 40 + 121 + . . . . + un _norte–1 + un _norte . . . .(1)

S = 1 + 4 + 13 + 40 + 121 + . . . . + un _norte–2 + un _norte–1 + un _norte . . . .(2)

Al restar (2) de (1), obtenemos

=> S – S = [1 + (4 + 13 + 40 + 121 + . . . . + un _n–1 + un _n )] – [(1 + 4 + 13 + 40 + 121 + . . . . + un _n–2 + un _n–1 ) + un _n ]

=> 0 = 1 + [(4 – 1) + (13 – 4) + (40 – 13) + . . . . + (un _norte – un _norte–1 )] – un _norte

=> un _norte = 1 + [3 + 9 + 27 + . . . . (n–1) términos]

Como la serie 3 + 9 + 27 + . . . . (n–1) términos es un GP, con el primer término (a) = 3 y la razón común (r) = 9/3 = 3. Entonces, obtenemos,

=> un _n = 1 + 3(3 ^n-1 –1)/(3–1)

= 1+ 3(3 ^n-1 –1)/2

= 1 + 3 ⁿ /2 – 3/2

= 3 ⁿ /2 – 1/2

Ahora tenemos que sumar nuestro ^enésimo término para encontrar la suma (S _n ) de esta serie.

$S_n = \sum_{k=1}^{n} a_k = \frac{1}{2}\sum_{k=1}^{n} 3^n - \frac{1}{2}\sum_{k=1}^{n} 1$

= $\frac{3^1+3^2+3^3+...+3^n}{2}-\frac{n}{2}$

= $\frac{3(3^n-1)}{(3-1)2}-\frac{n}{2}$

= $\frac{3(3^n)-2n-3}{4}$

= $\frac{3^{n+1}-2n-3}{4}$

Por tanto, la suma de la serie dada hasta n términos es $\frac{3^{n+1}-2n-3}{4}$ .

Pregunta 7. 4 + 6 + 9 + 13 + 18 + . . . . n términos

Solución:

Nos dan la serie: 4 + 6 + 9 + 13 + 18 + . . . . n términos.

Tomemos S como la suma de esta serie. Por lo tanto,

S = 4 + 6 + 9 + 13 + 18 + . . . . + un _norte–1 + un _norte . . . .(1)

S = 4 + 6 + 9 + 13 + 18 + . . . . + un _norte–2 + un _norte–1 + un _norte . . . .(2)

Al restar (2) de (1), obtenemos

=> S – S = [4 + (6 + 9 + 13 + 18 + . . . . + un _n–1 + un _n )] – [(4 + 6 + 9 + 13 + 18 + . . . . + un _n–2 + un _n–1 ) + un _n ]

=> 0 = 4 + [(6 – 4) + (9 – 6) + (13 – 9) + . . . . + (un _norte – un _norte–1 )] – un _norte

=> un _norte = 4 + [2 + 3 + 4 + . . . . (n–1) términos]

Como la serie 2 + 3 + 4 + . . . . (n–1) términos es un AP, con el primer término (a) = 2 y la diferencia común (d) = 3–2 = 1. Entonces, obtenemos,

=> un norte = 4 + ( _n –1) [2(2)+(n–2)1]/2

= 4 + (n–1)(n+2)/2

= $\frac{8+(n-1)(n+2)}{2}$

= $\frac{n^2+n+6}{2}$

Ahora tenemos que sumar nuestro ^enésimo término para encontrar la suma (S _n ) de esta serie.

$S_n = \sum_{k=1}^{n} a_k = \frac{1}{2}\left[\sum_{k=1}^{n} n^2 + \sum_{k=1}^{n} n + \sum_{k=1}^{n} 6\right]$

= $\frac{1}{2}\sum_{k=1}^{n} n^2 + \frac{1}{2}\sum_{k=1}^{n} n + \sum_{k=1}^{n} 3$

= $\frac{1}{2}[\frac{n(n+1)(2n+1)}{6}] + \frac{1}{2}[\frac{n(n+1)}{2}] + 3n$

= $\frac{n[(n+1)(2n+1)+3(n+1)+36]}{12}$

= $\frac{n[2n^2+6n+40]}{12}$

= $\frac{n[n^2+3n+20]}{6}$

Por tanto, la suma de la serie dada hasta n términos es $\frac{n[n^2+3n+20]}{6}$ .

Pregunta 8. 2 + 4 + 7 + 11 + 16 + . . . . n términos

Solución:

Nos dan la serie: 2 + 4 + 7 + 11 + 16 + . . . . n términos.

Tomemos S como la suma de esta serie. Por lo tanto,

S = 2 + 4 + 7 + 11 + 16 + . . . . + un _norte–1 + un _norte . . . .(1)

S = 2 + 4 + 7 + 11 + 16 + . . . . + un _norte–2 + un _norte–1 + un _norte . . . .(2)

Al restar (2) de (1), obtenemos

=> S – S = [2 + (4 + 7 + 11 + 16 + . . . . + un _n–1 + un _n )] – [(2 + 4 + 7 + 11 + 16 + . . . . + un _n–2 + un _n–1 ) + un _n ]

=> 0 = 2 + [(4 – 2) + (7 – 4) + (11 – 7) + . . . . + (un _norte – un _norte–1 )] – un _norte

=> un _norte = 2 + [2 + 3 + 4 + . . . . (n–1) términos]

Como la serie 2 + 3 + 4 + . . . . (n–1) términos es un AP, con el primer término (a) = 2 y la diferencia común (d) = 3–2 = 1. Entonces, obtenemos,

=> un norte = 2 + ( _n –1) [2(2)+(n–2)1]/2

= 2 + (n–1)(n+2)/2

= $\frac{4+n^2+2n-n-2}{2}$

= $\frac{n^2+n+2}{2}$

Ahora tenemos que sumar nuestro ^enésimo término para encontrar la suma (S _n ) de esta serie.

$S_n = \sum_{k=1}^{n} a_k = \frac{1}{2}\left[\sum_{k=1}^{n} n^2 + \sum_{k=1}^{n} n + \sum_{k=1}^{n} 2\right]$

= $\frac{1}{2}\sum_{k=1}^{n} n^2 + \frac{1}{2}\sum_{k=1}^{n} n + \sum_{k=1}^{n} 1$

= $\frac{1}{2}[\frac{n(n+1)(2n+1)}{6}]+\frac{1}{2}[\frac{n(n+1)}{2}]+n$

= $\frac{n[(n+1)(2n+1)+3(n+1)+12n]}{12}$

= $\frac{n(2n^2+6n+16)}{12}$

= $\frac{n(n^2+3n+8)}{6}$

Por tanto, la suma de la serie dada hasta n términos es $\frac{n(n^2+3n+8)}{6}$ .

Pregunta 9. 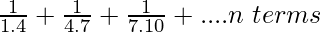$\frac{1}{1.4}+\frac{1}{4.7}+\frac{1}{7.10}+....n\hspace{0.1cm}terms$

Solución:

El n ^-ésimo término de la serie dada sería,

un _norte = $\frac{1}{(3n-2)(3n+1)}$

= $\frac{1}{3}\left[\frac{1}{3n-2}-\frac{1}{3n+1}\right]$

Ahora tenemos que sumar nuestro ^enésimo término para encontrar la suma (S _n ) de esta serie.

$S_n = \sum_{k=1}^{n} a_k = \frac{1}{3}\sum_{k=1}^{n} \left[\frac{1}{3n-2}-\frac{1}{3n+1}\right]$

= $\frac{1}{3}\left[(1-\frac{1}{4})+(\frac{1}{4}-\frac{1}{7})+(\frac{1}{7}-\frac{1}{10})...(\frac{1}{3n-2}-\frac{1}{3n+1})\right]$

= $\frac{1}{3}\left[1-\frac{1}{3n+1}\right]$

= $\frac{3n}{3(3n+1)}$

= $\frac{n}{3n+1}$

Por tanto, la suma de la serie dada hasta n términos es $\frac{n}{3n+1}$ .

Pregunta 10. 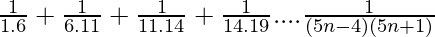$\frac{1}{1.6}+\frac{1}{6.11}+\frac{1}{11.14}+\frac{1}{14.19}....\frac{1}{(5n-4)(5n+1)}$ a n términos.

Solución:

Nos dan el ^enésimo término de la serie dada,

un _norte = $\frac{1}{(5n-4)(5n+1)}$

= $\frac{1}{5}\left[\frac{1}{5n-4}-\frac{1}{5n+1}\right]$

Ahora tenemos que sumar nuestro ^enésimo término para encontrar la suma (S _n ) de esta serie.

$S_n = \sum_{k=1}^{n} a_k = \frac{1}{5}\sum_{k=1}^{n} \left[\frac{1}{5n-4}-\frac{1}{5n+1}\right]$

= $\frac{1}{3}\left[(1-\frac{1}{6})+(\frac{1}{6}-\frac{1}{11})+(\frac{1}{11}-\frac{1}{14})...(\frac{1}{5n-4}-\frac{1}{5n+1})\right]$

= $\frac{1}{5}\left[1-\frac{1}{5n+1}\right]$

= $\frac{5n}{5(5n+1)}$

= $\frac{n}{5n+1}$

Por tanto, la suma de la serie dada hasta n términos es $\frac{n}{5n+1}$ .