Clase 11 Soluciones RD Sharma – Capítulo 22 Breve repaso del sistema cartesiano de coordenadas rectangulares – Ejercicio 22.2

Pregunta 1. Encuentra el lugar geométrico de un punto equidistante del punto (2, 4) y el eje y.

Solución:

Sea C (a, b) cualquier punto del lugar geométrico y sean A (2, 4) y B (0, b). Se nos da,

=> CA = CB

=> CA ² = CB ²

Usando la fórmula de la distancia, obtenemos,

=> (a – 2) ² + (b – 4) ² = (a – 0) ² + (b – b) ²

=> un ² + 4 − 4a + ^{segundo 2} + 16 − 8b = un ²

=> ^{segundo 2} − 4a − 8b + 20 = 0

Reemplazando (a, b) con (x, y), obtenemos el lugar geométrico de nuestro punto,

=> y ² − 4x − 8y + 20 = 0

Por lo tanto, el lugar geométrico del punto es y ² − 4x − 8y + 20 = 0.

Pregunta 2. Encuentra la ecuación del lugar geométrico de un punto que se mueve de tal manera que la razón de su distancia desde (2, 0) y (1, 3) es 5:4.

Solución:

Sea C (a, b) cualquier punto del lugar geométrico y sean A (2, 0) y B (1, 3). Se nos da,

=> CA/CB = 5/4

=> CA ² /CB ² = 25/16

Usando la fórmula de la distancia, obtenemos,

=> $\frac{(a-2)^2+(b-0)^2}{(a-1)^2+(b-3)^2}=\frac{25}{16}$

=> $\frac{a^2+4-4a+b^2}{a^2+1-2a+b^2+9-6b}=\frac{25}{16}$

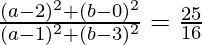
=> 16 (un ² + 4 − 4a + ^{segundo 2} ) = 25 (un ² + 1 − 2a + ^{segundo 2} + 9 − 6b)

=> 9a ² + 9b ² + 14a − 150b + 186 = 0

Reemplazando (a, b) con (x, y), obtenemos la ecuación del lugar geométrico de nuestro punto,

=> 9x ² + 9y ² + 14x − 150y + 186 = 0

Por tanto, el lugar geométrico del punto es 9x ² + 9y ² + 14x − 150y + 186 = 0.

Pregunta 3. Un punto se mueve de tal manera que la diferencia de sus distancias desde (ae, 0) y (−ae, 0) es 2a, demuestre que la ecuación de su lugar geométrico es x ² /a ² − y ² /b ² = 1, donde b ² = a ² (e ² − 1).

Solución:

Sea C (h, k) cualquier punto del lugar geométrico y sean A (ae, 0) y B (−ae, 0). Se nos da,

=> CA − CB = 2a

Usando la fórmula de la distancia, obtenemos,

=> $\sqrt{(h-ae)^2+(k-0)^2}-\sqrt{(h-(-ae))^2+(k-0)^2}=2a$

=> $\sqrt{(h-ae)^2+(k-0)^2}=2a+\sqrt{(h-(-ae))^2+(k-0)^2}$

Elevando al cuadrado ambos lados, obtenemos,

=> $(h-ae)^2+(k-0)^2=(2a+\sqrt{(h-(-ae))^2+(k-0)^2})^2$

=> h ² + un ^{2 mi}² − 2aeh + k ² = 4a ² + (h + ae) ² + k ² + $4a\sqrt{(h+ae)^2+(k-0)^2}$

=> h ² + un ^{2 mi}² − 2aeh + k ² = 4a ² + h ² + un ^{2 mi}² + 2aeh + k ² + $4a\sqrt{(h+ae)^2+(k-0)^2}$

=> −4aeh − 4a ² = $4a\sqrt{(h+ae)^2+(k-0)^2}$

Cuadrando ambos lados de nuevo, obtenemos,

=> −(eh + a) = (h + ae) ² + k ²

=> mi ² h ² + un ² + 2aeh = h ² + un ^{2 mi}² + 2aeh + k ²

=> h ² (e ² – 1) – k ² = a ² (e ² – 1)

=> $\frac{h^2}{a^2}-\frac{k^2}{a^2(e^2-1)}=1$

Como se nos da, b ² = a ² (e ² − 1), obtenemos,

=> h ² /a ² − k ² /b ² = 1

Reemplazando (h, k) con (x, y), obtenemos la ecuación del lugar geométrico de nuestro punto,

=> x ² /a ² − y ² /b ² = 1

Por lo tanto probado.

Pregunta 4. Encuentra el lugar geométrico de un punto tal que la suma de sus distancias desde (0, 2) y (0, −2) es 6.

Solución:

Sea C (a, b) cualquier punto del lugar geométrico y sean A (0, 2) y B (0, −2). Se nos da,

=> CA + CB = 6

Usando la fórmula de la distancia, obtenemos,

=> $\sqrt{(a-0)^2+(b-2)^2}+\sqrt{(a-0)^2+(b-(-2))^2}=6$

=> $\sqrt{(a-0)^2+(b-2)^2}=6-\sqrt{a^2+(b+2)^2}$

Elevando al cuadrado ambos lados, obtenemos,

=> un ² + ^{segundo 2} + 4 − 4b= 36 + un ² + ^{segundo 2} + 4 + 4b − $12\sqrt{a^2+(b+2)^2}$

=> −8b − 36 = $-12\sqrt{a^2+(b+2)^2}$

=> −4 (2b + 9) = $-12\sqrt{a^2+(b+2)^2}$

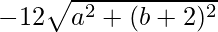
Cuadrando ambos lados de nuevo, obtenemos,

=> (2b + 9) ² = $(3\sqrt{a^2+(b+2)^2})^2$

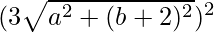
=> 4b ² + 81 + 36b = 9a ² + 9b ² + 36b + 36

=> 9a ² + 5b ² = 45

Reemplazando (a, b) con (x, y), obtenemos el lugar geométrico de nuestro punto,

=> 9×2 ⁺ 5y2 ⁼ 45

Por lo tanto el lugar geométrico del punto es 9x ² + 5y ² = 45.

Pregunta 5. Encuentra el lugar geométrico de un punto que es equidistante de (1, 3) y el eje x.

Solución:

Sea C (a, b) cualquier punto del lugar geométrico y sean A (1, 3) y B (a, 0). Se nos da,

=> CA = CB

=> CA ² = CB ²

Usando la fórmula de la distancia, obtenemos,

=> (a – 1) ² + (b – 3) ² = (a – a) ² + (b – 0) ²

=> un ² + 1 − 2a + ^{segundo 2} + 9 − 6b = ^{segundo 2}

=> un ² − 2a − 6b + 10 = 0

Reemplazando (a, b) con (x, y), obtenemos el lugar geométrico de nuestro punto,

=> x2 − ^2x − 6y + 10 = 0

Por lo tanto, el lugar geométrico del punto es x ² − 2x − 6y + 10 = 0.

Pregunta 6. Encuentra el lugar geométrico de un punto que se mueve de tal manera que su distancia desde el origen es tres veces su distancia desde el eje x.

Solución:

Sea C (a, b) cualquier punto del lugar geométrico y sean A (0, 0) y B (a, 0). Se nos da,

=> CA = 3 BC

=> CA ² = 9 CB ²

Usando la fórmula de la distancia, obtenemos,

=> (a – 0) ² + (b – 0) ² = 9 [(a – a) ² + (b – 0) ² ]

=> un ² + ^{segundo 2} = 9b ²

=> un ² = 8b ²

Reemplazando (a, b) con (x, y), obtenemos el lugar geométrico de nuestro punto,

=> ^x2 = ^8y2

Por lo tanto el lugar geométrico del punto es x ² = 8y ² .

Pregunta 7. A (5, 3), B (3, −2) son dos puntos fijos, encuentre la ecuación del lugar geométrico de un punto P que se mueve de modo que el área del triángulo PAB es de 9 unidades cuadradas.

Solución:

Sea P (a, b) cualquier punto del lugar geométrico y tenemos A (5, 3) y B (3, −2). Se nos da,

=> Área del triángulo PAB = 9

=> $\frac{1}{2}|x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)|=9$

=> |5(−2−b) + 3(b−3) + h(3+2)| = 18

=> |5a − 2b − 19| = 18

=> 5a − 2b − 19 = ±18

=> 5a − 2b − 37 = 0 o 5a − 2b − 1 = 0

Reemplazando (a, b) con (x, y), obtenemos el lugar geométrico de nuestro punto,

=> 5x − 2y − 37 = 0 o 5x − 2y − 1 = 0

Por lo tanto, la ecuación del lugar geométrico del punto es 5x − 2y − 37 = 0 o 5x − 2y − 1 = 0.

Pregunta 8. Encuentra el lugar geométrico de un punto tal que el segmento de línea que tiene los extremos (2, 0) y (−2, 0) subtiende un ángulo recto en ese punto.

Solución:

Sea C (a, b) cualquier punto del lugar geométrico y sean A (2, 0) y B (−2, 0).

Nos dan ∠ ACB = 90 ^o

=> AB ² = CA ² + CB ²

Usando la fórmula de la distancia, obtenemos,

=> (2+2) ² + (0−0) ² = (a−2) ² + (b−0) ² + (a+2) ² + (b−0) ²

=> 16 = un ² + 4 − 4a + ^{segundo 2} + un ² + 4 + 4a + ^{segundo 2}

=> 2a ² + 2b ² + 8 = 16

=> un ² + ^{segundo 2} = 4

Reemplazando (a, b) con (x, y), obtenemos el lugar geométrico de nuestro punto,

=> x2 + ^y2 = ⁴

Por lo tanto, el lugar geométrico del punto es x ² + y ² = 4.

Pregunta 9. A (−1, 1), B (2, 3) son dos puntos fijos, encuentre el lugar geométrico de un punto P que se mueve de modo que el área del triángulo PAB es de 8 unidades cuadradas.

Solución:

Sea P (a, b) cualquier punto del lugar geométrico y tenemos A (−1, 1) y B (2, 3). Se nos da,

=> Área del triángulo PAB = 8

=> $\frac{1}{2}|x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)|=8$

=> |−1(3−b) + 2(b−1) + a(1−3)| = 16

=> |−2a + 3b − 5| = 16

=> −2a + 3b − 5 = ±16

=> 2a − 3b + 21 = 0 o 2a − 3b − 11 = 0

Reemplazando (a, b) con (x, y), obtenemos el lugar geométrico de nuestro punto,

=> 2x − 3y + 21 = 0 o 2x − 3y − 11 = 0

Por lo tanto, el lugar geométrico del punto es 2x − 3y + 21 = 0 o 2x − 3y − 11 = 0.

Pregunta 10. Una barra de longitud l se desliza entre dos líneas perpendiculares. Encuentra el lugar geométrico del punto de la barra que la divide en la razón 1:2.

Solución:

Sea C (h, k) cualquier punto en el lugar geométrico y sea AB = l (dado) la longitud de la barra. Supongamos que las coordenadas de A y B son (a, 0) y (0, b) respectivamente.

Según la pregunta,

=> h = 2a/3

=> a = 3h/2 . . . . (1)

y k = b/3

=> segundo = 3k. . . . (2)

Sea el origen O (0, 0). Ahora sabemos que △ AOB tiene un ángulo recto.

=> AB ² = OA ² + OB ²

=> l ² = [(a−0) ² + (0−0) ² ] + [(0−0) ² + (b−0) ² ]

=> un ² + ^{segundo 2} = l ²

Usando (1) y (2), obtenemos,

=> (3h/2) ² + (3k) ² = l ²

=> 9h ² /4 + 9k ² = l ²

=> 9h ² + 36k ² = 4l ²

Reemplazando (h, k) con (x, y), obtenemos el lugar geométrico de nuestro punto,

=> 9x ² + 36y ² = 4l ²

Por lo tanto el lugar geométrico del punto es 9x ² + 36y ² = 4l ² .

Pregunta 11. Encuentra el lugar geométrico del punto medio de la porción de la línea x cos α + y sin α = p que es interceptada entre los ejes.

Solución:

Se nos da,

=> x cos α + y sen α = p

=> $\frac{x}{\frac{p}{cos α}}+\frac{y}{\frac{p}{sin α}}=1$

Las intersecciones en el eje x y el eje y son p/cos α y p/sen α respectivamente.

Supongamos que (x, y) es el punto medio de la porción de la línea dada que es interceptada entre los ejes.

=> (x, y) = $\left(\frac{\frac{p}{cosα}+0}{2},\frac{\frac{p}{sinα}+0}{2}\right)=\left(\frac{p}{2cosα},\frac{p}{2sinα}\right)$

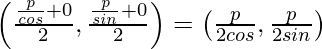
=> x = p/2 cos α y y = p/2 sen α

=> 2 cos α = p/x y 2 sen α = p/y

Cuadrando ambos lados de estos, obtenemos,

=> 4 porque ² α = pags ² /x ² . . . . (1)

=> 4 sen ² α = pags ² /y ² . . . . (2)

Sumando (1) y (2), obtenemos,

=> 4 cos ² α + 4 sen ² α = p ² /x ² + p ² /y ²

=> pag ² /x ² + pag ² /y ² = 4

=> pag ² (x ² + y ² ) = 4x ² y ²

Por lo tanto, el lugar geométrico del punto medio es p ² (x ² + y ² ) = 4x ² y ² .

Pregunta 12. Si O es el origen y Q es el punto variable en y ² = x. Encuentre el lugar geométrico del punto medio de OQ.

Solución:

Sea P (h, k) el punto sobre el lugar geométrico y sea Q (a, b).

Según la pregunta,

=> h = (a+0)/2 y k = (b+0)/2

=> h = a/2 y k = b/2

=> a = 2h y b = 2k

Como el punto Q se encuentra en y ² = x, obtenemos,

=> (2k) ² = 2h

=> 4k ² = 2h

=> 2k ² = hora

Reemplazando (h, k) con (x, y), obtenemos el lugar geométrico de nuestro punto,

=> 2y ² = x

Por lo tanto, el lugar geométrico del punto medio es 2y ² = x.

Publicación traducida automáticamente

Artículo escrito por gurjotloveparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1. Encuentra el lugar geométrico de un punto equidistante del punto (2, 4) y el eje y.

Pregunta 2. Encuentra la ecuación del lugar geométrico de un punto que se mueve de tal manera que la razón de su distancia desde (2, 0) y (1, 3) es 5:4.

Pregunta 3. Un punto se mueve de tal manera que la diferencia de sus distancias desde (ae, 0) y (−ae, 0) es 2a, demuestre que la ecuación de su lugar geométrico es x 2 /a 2 − y 2 /b 2 = 1, donde b 2 = a 2 (e 2 − 1).

Pregunta 4. Encuentra el lugar geométrico de un punto tal que la suma de sus distancias desde (0, 2) y (0, −2) es 6.

Pregunta 5. Encuentra el lugar geométrico de un punto que es equidistante de (1, 3) y el eje x.

Pregunta 6. Encuentra el lugar geométrico de un punto que se mueve de tal manera que su distancia desde el origen es tres veces su distancia desde el eje x.

Pregunta 7. A (5, 3), B (3, −2) son dos puntos fijos, encuentre la ecuación del lugar geométrico de un punto P que se mueve de modo que el área del triángulo PAB es de 9 unidades cuadradas.

Pregunta 8. Encuentra el lugar geométrico de un punto tal que el segmento de línea que tiene los extremos (2, 0) y (−2, 0) subtiende un ángulo recto en ese punto.

Pregunta 9. A (−1, 1), B (2, 3) son dos puntos fijos, encuentre el lugar geométrico de un punto P que se mueve de modo que el área del triángulo PAB es de 8 unidades cuadradas.

Pregunta 10. Una barra de longitud l se desliza entre dos líneas perpendiculares. Encuentra el lugar geométrico del punto de la barra que la divide en la razón 1:2.

Pregunta 11. Encuentra el lugar geométrico del punto medio de la porción de la línea x cos α + y sin α = p que es interceptada entre los ejes.

Pregunta 12. Si O es el origen y Q es el punto variable en y 2 = x. Encuentre el lugar geométrico del punto medio de OQ.

Deja una respuesta Cancelar la respuesta

Pregunta 3. Un punto se mueve de tal manera que la diferencia de sus distancias desde (ae, 0) y (−ae, 0) es 2a, demuestre que la ecuación de su lugar geométrico es x ² /a ² − y ² /b ² = 1, donde b ² = a ² (e ² − 1).

Pregunta 12. Si O es el origen y Q es el punto variable en y ² = x. Encuentre el lugar geométrico del punto medio de OQ.