Clase 11 Soluciones RD Sharma – Capítulo 22 Breve repaso del sistema cartesiano de coordenadas rectangulares – Ejercicio 22.3

Pregunta 1. ¿En qué se convierte la ecuación (x – a) ² + (y – b) ² = r ² cuando los ejes se transfieren a ejes paralelos a través del punto (a–c, b)?

Solución:

Se nos da,

(x – a) ² + (y – b) ² = r ²

Poniendo x = X + a – c y y = Y + b, obtenemos,

=> ((X + a – c) – a) ² + ((Y + b ) – b) ² = r ²

=> (X – c) ² + Y ² = r ²

=> X ² + c ² – 2cX + Y ² = r ²

=> X ² + Y ² – 2cX = r ² – c ²

Por lo tanto, la ecuación requerida es X ² + Y ² – 2cX = r ² – c ² .

Pregunta 2. ¿En qué se convierte la ecuación (a – b) (x ² + y ² ) – 2abx = 0 si el origen se desplaza al punto (ab/(a–b), 0) sin rotación?

Solución:

Se nos da,

(a – b) (x ² + y ² ) – 2abx = 0

Poniendo x = X + [ab/(a–b)] y y = Y, obtenemos,

=> $(a - b)\left[\left(X+\frac{ab}{a+b}\right)^2 + Y^2\right] - 2ab\left(X+\frac{ab}{a+b}\right) = 0$

=> $(a-b)\left[X^2+\left(\frac{ab}{a+b}\right)^2+2\frac{Xab}{a+b}+Y^2\right]-2abX-2\frac{(ab)^2}{a-b} = 0$

=> $(a-b)\left[\frac{X^2(a-b)^2+(ab)^2+2Xab(a-b)+Y^2(a-b)^2}{(a-b)^2}\right]-\frac{2abX(a-b)+2(ab)^2}{a-b}= 0$

=> $\frac{X^2(a-b)^2+(ab)^2+2Xab(a-b)+Y^2(a-b)^2}{a-b}=\frac{2abX(a-b)+2(ab)^2}{a-b}$

=> X ² (a–b) ² + (ab) ² + 2abX (a–b)+Y ² (a–b) ² = 2abX (a–b)+2(ab) ²

=> (a – b) ² (X ² + Y ² ) = a ² b ²

Por lo tanto, la ecuación requerida es (a – b) ² (X ² + Y ² ) = a ² b ² .

Pregunta 3. ¿Encuentra en qué se convierten las siguientes ecuaciones cuando el origen se desplaza al punto (1, 1)?

(i) x ² + xy – 3x – y + 2 = 0

Solución:

Se nos da,

x ² + xy – 3x – y + 2 = 0

Poniendo x = X + 1 y y = Y + 1, obtenemos,

=> (X + 1) ² + (X + 1) (Y + 1) – 3(X + 1) – (Y + 1) + 2 = 0

=> X ² + 1 + 2X + XY + X + Y + 1 – 3X – 3 – Y – 1 + 2 = 0

Por lo tanto, la ecuación requerida es X ² + XY = 0.

(ii) x ² – y ² – 2x + 2y = 0

Solución:

Se nos da,

x ² – y ² – 2x + 2y = 0

Poniendo x = X + 1 y y = Y + 1, obtenemos,

=> (X + 1) ² – (Y + 1) ² – 2(X + 1) + 2(Y + 1) = 0

=> X ² + 1 + 2X – Y ² – 1 – 2Y – 2X – 2 + 2Y + 2 = 0

= > X2 – Y2 ⁼⁰

Por lo tanto, la ecuación requerida es X ² – Y ² = 0.

(iii) xy – x – y + 1 = 0

Solución:

Se nos da,

xy – x – y + 1 = 0

Poniendo x = X + 1 y y = Y + 1, obtenemos,

=> (X + 1) (Y + 1) – (X + 1) – (Y + 1) + 1 = 0

=> XY + X + Y + 1 – X – 1 – Y – 1 + 1 = 0

=> XY = 0

Por lo tanto, la ecuación requerida es XY = 0.

(iv) xy – y ² – x + y = 0

Solución:

Se nos da,

xy – y ² – x + y = 0

Poniendo x = X + 1 y y = Y + 1, obtenemos,

=> (X + 1) (Y + 1) – (Y + 1) ² – (X + 1) + (Y + 1) = 0

=> XY + X + Y + 1 – Y ² – 1 – 2Y – X – 1 + Y + 1 = 0

=> XY-Y2 = ⁰

Por lo tanto, la ecuación requerida es XY – Y ² = 0.

Pregunta 4. ¿En qué punto se desplaza el origen para que la ecuación x ² + xy – 3x – y + 2 = 0 no contenga ningún término de primer grado ni término constante?

Solución:

Se nos da,

x ² + xy – 3x – y + 2 = 0

Supongamos que (a, b) es el punto donde el origen se ha desplazado desde (0, 0). Poniendo x = X + a y y = Y + b, obtenemos la ecuación transformada,

=> (X + a) ² + (X + a)(Y + b) – 3(X + a) – (Y + b) + 2 = 0

=> X ² + a ² + 2aX + XY + aY + bX + ab – 3X – 3a – Y – b + 2 = 0

=> X2 ⁺ XY + X(2a + b – 3) + Y(a – 1) + a ² + ab – 3a – b + 2 = 0

Como nuestra ecuación transformada no tiene término de primer grado, tenemos,

2a + b – 3 = 0 y a – 1 = 0

Resolviendo estas ecuaciones tenemos a = 1 y b = 1.

Por lo tanto, el origen se ha desplazado a (1,1) desde (0,0).

Pregunta 5. Verifique que el área del triángulo con vértices (2, 3), (5, 7) y (–3, –1) permanece invariante bajo la traslación de ejes cuando el origen se desplaza al punto (–1 , 3).

Solución:

Aquí, LHS = A ₁ = Área del triángulo con vértices (2, 3), (5, 7) y (–3, –1)

= $\frac{1}{2}|x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)|$

= $\frac{1}{2}|2(7+1)+5(-1-3)-3(3-7)|$

= $\frac{1}{2}|16-20-12|$

= $\frac{8}{2}$

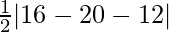
= 4 unidades cuadradas

Como el origen se desplazó al punto (–1, 3), las nuevas coordenadas del triángulo son:

(X ₁ , Y ₁ ) = (2–1, 3+3) = (1, 6)

(X ₂ , Y ₂ ) = (5–1, 7+3) = (4, 10)

(X ₃ , Y ₃ ) = (–3–1, –1+3) = (–4, 2)

Ahora, RHS = A ₂ = Área del triángulo con vértices (1, 6), (4, 10) y (–4, 2)

= $\frac{1}{2}|X_1(Y_2-Y_3)+X_2(Y_3-Y_1)+X_3(Y_1-Y_2)|$

= $\frac{1}{2}|1(10-2)+4(2-6)-4(6-10)|$

= $\frac{1}{2}|8-16+16|$

= $\frac{8}{2}$

= 4 unidades cuadradas

Por lo tanto, A ₁ = A ₂ .

Por lo tanto, probado.

Pregunta 6. ¿Encuentra en qué se convierten las siguientes ecuaciones cuando el origen se desplaza al punto (1, 1)?

(i) x ² + xy – 3y ² – y + 2 = 0

Solución:

Se nos da,

x ² + xy – 3y ² – y + 2 = 0

Poniendo x = X + 1 y y = Y + 1, obtenemos,

=> (X + 1) ² + (X + 1) (Y + 1) – 3(Y + 1) ² – (Y + 1) + 2 = 0

=> X ² + 1 + 2X + XY + X + Y + 1 – 3Y ² – 3 – 6Y – Y – 1 + 2 = 0

=> X ² – 3Y ² + XY + 3X – 6Y = 0

Por lo tanto, la ecuación requerida es X ² – 3Y ² + XY + 3X – 6Y = 0.

(ii) xy – y ² – x + y = 0

Solución:

Se nos da,

xy – y ² – x + y = 0

Poniendo x = X + 1 y y = Y + 1, obtenemos,

=> (X + 1) (Y + 1) – (Y + 1) ² – (X + 1)+ Y + 1 = 0

=> XY + X + Y + 1 – Y ² – 1 – 2Y – X – 1 + Y + 1 = 0

=> XY-Y2 = ⁰

Por lo tanto, la ecuación requerida es XY – Y ² = 0.

(iii) xy – x – y + 1 = 0

Solución:

Se nos da,

xy – x – y + 1 = 0

Poniendo x = X + 1 y y = Y + 1, obtenemos,

=> (X + 1) (Y + 1) – (Y + 1) – (X + 1) + 1 = 0

=> XY + X + Y + 1 – Y – 1 – X – 1 + 1 = 0

=> XY = 0

Por lo tanto, la ecuación requerida es XY = 0.

(iv) x ² – y ² – 2x + 2y = 0

Solución:

Se nos da,

x ² – y ² – 2x + 2y = 0

Poniendo x = X + 1 y y = Y + 1, obtenemos,

=> (X + 1) ² – (Y + 1) ² – 2(X + 1) + 2(Y + 1) = 0

=> X ² + 1 + 2X – Y ² – 1 – 2Y – 2X – 2 + 2Y + 2 = 0

= > X2 – Y2 ⁼⁰

Por lo tanto, la ecuación requerida es X ² – Y ² = 0.

Pregunta 7. Encuentre el punto al que se debe desplazar el origen después de la traslación de los ejes para que las siguientes ecuaciones no tengan términos de primer grado.

(i) x2 + ^{y2 – 4x – 8y}⁺ 3 = 0

Solución:

Se nos da,

x2 + ^{y2 – 4x – 8y}⁺ 3 = 0

Supongamos que (a, b) es el punto donde el origen se ha desplazado desde (0, 0). Poniendo x = X + a y y = Y + b, obtenemos la ecuación transformada,

=> (X + a) ² + (Y + b) ² – 4(X + a) – 8(Y + b) + 3 = 0

=> X2 ⁺ a2 + ^2aX + Y2 ⁺ b2 ⁺ 2bY – 4X – 4a – 8Y – 8b + 3 = 0

=> X ² + Y ² + (2a – 4) X + (2b – 8) Y + (a ² + b ² – 4a – 8b +3) = 0

Como nuestra ecuación transformada no tiene término de primer grado, tenemos,

2a – 4 = 0 y 2b – 8 = 0

Resolviendo estas ecuaciones tenemos a = 2 y b = 4.

Por lo tanto, el origen se ha desplazado a (2,4) desde (0,0).

(ii) x2 + ^{y2 – 5x +}^2y – 5 = 0

Solución:

Se nos da,

x2 + ^{y2 – 5x +}^2y – 5 = 0

Supongamos que (a, b) es el punto donde el origen se ha desplazado desde (0, 0). Poniendo x = X + a y y = Y + b, obtenemos la ecuación transformada,

=> (X + a) ² + (Y + b) ² – 5(X + a) + 2(Y + b) – 5 = 0

=> X2 ⁺ a2 + ^2aX + Y2 ⁺ b2 ⁺ 2bY – 5X – 5a + 2Y + 2b – 5 = 0

=> X ² + Y ² + (2a – 5) X + (2b + 2) Y + (a ² + b ² – 5a + 2b – 5) = 0

Como nuestra ecuación transformada no tiene término de primer grado, tenemos,

2a – 5 = 0 y 2b + 2 = 0

Resolviendo estas ecuaciones tenemos a = 5/2 yb = –1.

Por lo tanto, el origen se ha desplazado a (5/2, –1) desde (0,0).

(iii) x ² – 12x + 4 = 0

Solución:

Se nos da,

x ² – 12x + 4 = 0

Supongamos que (a, b) es el punto donde el origen se ha desplazado desde (0, 0). Poniendo x = X + a y y = Y + b, obtenemos la ecuación transformada,

=> (X + a) ² – 12(X + a) + 4 = 0

=> X ² + a ² + 2aX – 12X – 12a + 4 = 0

=> X2 ⁺ (2a – 12)X + ( ^a2 – 12a + 4) = 0

Como nuestra ecuación transformada no tiene término de primer grado, tenemos,

=> 2a – 12 = 0

=> un = 6

Por lo tanto, el origen se ha desplazado a (6,b) desde (0,0) donde b es cualquier valor arbitrario.

Pregunta 8. Verifique que el área del triángulo con vértices (4, 6), (7, 10) y (1, –2) permanece invariante bajo la traslación de ejes cuando el origen se desplaza al punto (–2, 1).

Solución:

Aquí, LHS = A ₁ = Área del triángulo con vértices (4, 6), (7, 10) y (1, –2)

= $\frac{1}{2}|x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)|$

= $\frac{1}{2}|4(10+2)+7(-2-6)+1(6-10)|$

= $\frac{1}{2}|48-56-4|$

= $\frac{12}{2}$

= 6 unidades cuadradas

Como el origen se desplazó al punto (–2, 1), las nuevas coordenadas del triángulo son:

(X ₁ , Y ₁ ) = (4–2, 6+1) = (2, 7)

(X ₂ , Y ₂ ) = (7–2, 10+1) = (5, 11)

(X ₃ , Y ₃ ) = (1–2, –2+1) = (–1, –1)

Ahora, RHS = A ₂ = Área del triángulo con vértices (2, 7), (5, 11), (–1, –1)

= $\frac{1}{2}|X_1(Y_2-Y_3)+X_2(Y_3-Y_1)+X_3(Y_1-Y_2)|$

= $\frac{1}{2}|2(11+1)+5(-1-7)-1(7-11)|$

= $\frac{1}{2}|24-40+4|$

= $\frac{12}{2}$

= 6 unidades cuadradas

Por lo tanto, A ₁ = A ₂ .

Por lo tanto, probado.

Publicación traducida automáticamente

Artículo escrito por gurjotloveparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1. ¿En qué se convierte la ecuación (x – a) 2 + (y – b) 2 = r 2 cuando los ejes se transfieren a ejes paralelos a través del punto (a–c, b)?

Pregunta 2. ¿En qué se convierte la ecuación (a – b) (x 2 + y 2 ) – 2abx = 0 si el origen se desplaza al punto (ab/(a–b), 0) sin rotación?

Pregunta 3. ¿Encuentra en qué se convierten las siguientes ecuaciones cuando el origen se desplaza al punto (1, 1)?

(i) x 2 + xy – 3x – y + 2 = 0

(ii) x 2 – y 2 – 2x + 2y = 0

(iii) xy – x – y + 1 = 0

(iv) xy – y 2 – x + y = 0

Pregunta 4. ¿En qué punto se desplaza el origen para que la ecuación x 2 + xy – 3x – y + 2 = 0 no contenga ningún término de primer grado ni término constante?

Pregunta 5. Verifique que el área del triángulo con vértices (2, 3), (5, 7) y (–3, –1) permanece invariante bajo la traslación de ejes cuando el origen se desplaza al punto (–1 , 3).

Pregunta 6. ¿Encuentra en qué se convierten las siguientes ecuaciones cuando el origen se desplaza al punto (1, 1)?

(i) x 2 + xy – 3y 2 – y + 2 = 0

(ii) xy – y 2 – x + y = 0

(iii) xy – x – y + 1 = 0

(iv) x 2 – y 2 – 2x + 2y = 0

Pregunta 7. Encuentre el punto al que se debe desplazar el origen después de la traslación de los ejes para que las siguientes ecuaciones no tengan términos de primer grado.

(i) x2 + y2 – 4x – 8y + 3 = 0

(ii) x2 + y2 – 5x + 2y – 5 = 0

(iii) x 2 – 12x + 4 = 0

Pregunta 8. Verifique que el área del triángulo con vértices (4, 6), (7, 10) y (1, –2) permanece invariante bajo la traslación de ejes cuando el origen se desplaza al punto (–2, 1).

Deja una respuesta Cancelar la respuesta

Pregunta 1. ¿En qué se convierte la ecuación (x – a) ² + (y – b) ² = r ² cuando los ejes se transfieren a ejes paralelos a través del punto (a–c, b)?

Pregunta 2. ¿En qué se convierte la ecuación (a – b) (x ² + y ² ) – 2abx = 0 si el origen se desplaza al punto (ab/(a–b), 0) sin rotación?

(i) x ² + xy – 3x – y + 2 = 0

(ii) x ² – y ² – 2x + 2y = 0

(iv) xy – y ² – x + y = 0

Pregunta 4. ¿En qué punto se desplaza el origen para que la ecuación x ² + xy – 3x – y + 2 = 0 no contenga ningún término de primer grado ni término constante?

(i) x ² + xy – 3y ² – y + 2 = 0

(ii) xy – y ² – x + y = 0

(iv) x ² – y ² – 2x + 2y = 0

(i) x2 + ^{y2 – 4x – 8y}⁺ 3 = 0

(ii) x2 + ^{y2 – 5x +}^2y – 5 = 0

(iii) x ² – 12x + 4 = 0