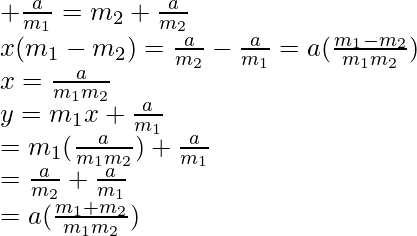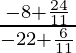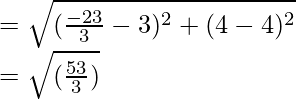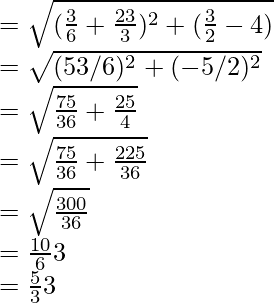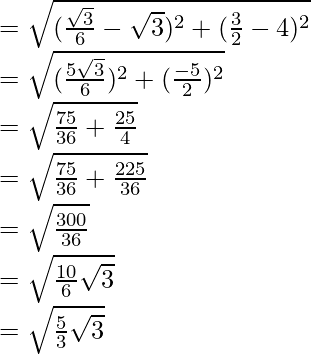Pregunta 1. (i) Encuentra el punto de intersección de las líneas:
2x – y + 3 = 0 y x + y – 5 = 0
Solución:
Dada la ecuación de las líneas son:
2x – y + 3 = 0 …..(1)
x + y – 5 = 0 ……(2)
2x – y + 3 = 0
⇒ y = 2x + 3
Ahora ponga este valor en la ecuación (2), obtenemos
x + y – 5 = 0
x + (2x + 3) – 5 = 0
x + 2x + 3 – 5 = 0
3x – 2 = 0
X = 2/3
Ahora pon el valor de x en la ecuación (1), obtenemos
y = 2x + 3 = (2 × 2)/3 + 3 = 4/3 + 3 = 13/2
Por lo tanto, los puntos de intersección son (2/3, 13/3)
Pregunta 1(ii). Encuentre el punto de intersección de los pares de líneas:
bx + ay = ab y ax + by = ab
Solución:
Dada la ecuación de las líneas son:
bx + ay = ab …..(1)
hacha + por = ab …..(2)
bx + ay = ab ⇒
Ahora ponga este valor en la ecuación (2), obtenemos
hacha + por = ab
a((ab – ay)/(b)) + por = ab
un 2 segundo – un 2 y + segundo 2 y = un 2
y(b 2 – a 2 ) = ab(b – a)
Ahora pon el valor de x en la ecuación (1), obtenemos
Por lo tanto, los puntos de intersección son (
)
(iii) Encuentre el punto de intersección de los pares de líneas:
y = m 1 x + a/m 1 y y = m 2 x + a/m 2
Solución:
Dada la ecuación de las líneas son:
y = m 1 x + a/m 1 …..(1)
y = m 2 x + a/m 2 …..(2)
De la ecuación (1) y (2)
m1x
Por lo tanto, el punto de intersección es
Pregunta 2 (i). Halla las coordenadas de los vértices de un triángulo cuyas ecuaciones sean x + y – 4 = 0, 2x – y + 3 = 0 y x – 3y + 2 = 0.
Solución:
Ecuaciones dadas:
x + y – 4 = 0 …..(1)
2x – y + 3 = 0 …..(2)
x – 3y + 2 = 0 …..(3)
Al resolver la ecuación (1) y (2)
2x – (4 – x) + 3 = 0
2x – 4 + x + 3 = 0
3x – 1 = 0
X = 1/3
Ahora pon el valor de x en la ecuación (1), obtenemos
1/3 + y – 4 = 0
y = 4 – 1/3 = 11/3
Entonces, el primer vértice es (1/3, 11/3)
Al resolver las ecuaciones (2) y (3), y
Ponga y = 2x + 3 en la ecuación (3)
x – 3(2x + 3) + 2 = 0
x-6y-9 + 2 = 0
-5x = 7
x = -7/5
y = 2x + 3 = 2(-7/5) + 3 = -14/5 + 3 = 1/5
Entonces, el segundo vértice es (-7/5, 1/5)
Ahora encontramos el siguiente vértice.
x + y – 4 = 0
x – 3y + 2 = 0
x = 4 – y
4 – y – 3y + 2 = 0
4 – 4 años + 2 = 0
-4y = -6
y = 3/2
x = 4 – y
4 – 3/2
8 – 3/2 = 5/2
Por lo tanto, el tercer vértice es (5/2, 3/2)
Pregunta 2 (ii). Encuentre las coordenadas de los vértices de un triángulo, la ecuación de cuyos lados son y(t 1 + t 2 ) = 2x + 2at 1 t 2 , y(t 2 + t 3 ) = 3x + 2at 2 t 3 y y( t 3 + t 1 ) = 2x + 2a + t 1 t 3
Solución:
Ecuaciones dadas:
y(t 1 + t 2 ) = 2x + 2 en 1 t 2 …..(1)
y(t 2 + t 3 ) = 2x + 2 en 2 t 3 …..(2)
y(t 3 + t 1 ) = 2x + 2 en 1 t 3 …..(3)
Al resolver las ecuaciones (1) y (2), obtenemos
(x 1 , y 1 ) = (en 2 2 , 2 en 2 )
Al resolver las ecuaciones (2) y (3), obtenemos
(x 2 , y 2 ) = (en 3 2 , 2 en 3 )
Al resolver las ecuaciones (1) y (3), obtenemos
(x 3 , y 3 ) = (en 1 2 , 2 en 1 )
Por lo tanto, los vértices del triángulo son (en 2 2 , 2en 2 ), (en 3 2 , 2en 3 ) y (en 1 2 , 2en 1 ).
Pregunta 3 (i). Halla el área del triángulo formado por las rectas
y = metro 1 + do 1 , y = metro 2 + do 2 , x = 0
Solución:
Ecuaciones dadas
y = metro 1 x + c 1 …..(1)
y = metro 2 x + c 2 …..(2)
x = 0 …..(3)
Al resolver las ecuaciones (1) y (2), obtenemos
(x 1 , y 1 ) = (
)
Al resolver las ecuaciones (2) y (3), obtenemos
(x 2 , y 2 ) = (0, c 2 )
Al resolver las ecuaciones (1) y (3), obtenemos
(x 3 , y 3 ) = (0, c 1 )
El área del triángulo formado por los vértices anteriores es
unidades cuadradas
Pregunta 3 (ii). Halla el área del triángulo formado por las rectas
y = 0, x = 2 y x + 2y = 3
Solución:
Ecuaciones dadas
y = 0 …..(1)
x = 2 …..(2)
x + 2y = 3 …..(3)
Al resolver las ecuaciones (1) y (2), obtenemos
Punto (x 1 , y 1 ) = (2, 0)
Al resolver las ecuaciones (2) y (3), obtenemos
2 + 2y = 3
y = 1/2
y = 2
Punto (x 2 , y 2 ) = (2, 1/2)
Al resolver las ecuaciones (1) y (3), obtenemos
Punto (x 3 , y 3 ) = (3, 0)
Como sabemos que el área del triángulo es (A) = 1/2[x 1 (y 2 – y 3 ) + x 2 (y 3 – y 1 ) + x 3 (y 1 – y 2 )]
A = 1/2[2(1/2 – 0) + 2(0 – 0) + 3( 0 – 1/2)]
A = 1/2[|1 – 3/2|]
A = 1/4 unidades cuadradas
Pregunta 3 (iii). Halla el área del triángulo formado por las rectas
x + y – 6 = 0, x – 3y – 2 = 0 y 5x – 3y + 2 = 0
Solución:
Ecuaciones dadas
x + y – 6 = 0 …..(1)
x – 3y – 2 = 0 …..(2)
5x – 3y + 2 = 0 …..(3)
Al resolver las ecuaciones (1) y (2), obtenemos
(x 1 , y 1 ) = (5, 1)
Al resolver las ecuaciones (2) y (3), obtenemos
(x 2 , y 2 ) = (-1, -1)
Al resolver las ecuaciones (3) y (1), obtenemos
(x 3 , y 3 ) = (2, 4)
Como sabemos que el área del triángulo es (A) = 1/2[x 1 (y 2 – y 3 ) + x 2 (y 3 – y 1 ) + x 3 (y 1 – y 2 )]
A = 1/2[|-25 – 3 + 4|]
A = 12 unidades cuadradas
Pregunta 4. Encuentra la ecuación de las medianas de un triángulo, la ecuación de cuyos lados son:
3x + 2y + 6 = 0, 2x – 5y + 4 = 0, x – 3y – 6 = 0
Solución:
Consideremos que ABC es un triángulo, en el que A, B y C son los vértices del triángulo.
Entonces, de acuerdo con la pregunta, las ecuaciones son:
3x + 2y + 6 = 0 …..(1)
2x – 5y + 4 = 0 …..(2)
x – 3y – 6 = 0 …..(3)
Al resolver las ecuaciones (1) y (2), obtenemos
x = -2 y y = 0
Entonces las coordenadas de A son (-2, 0)
Al resolver la ecuación (3) y (2), obtenemos
x = -42 y y = -16
Entonces las coordenadas de B son (-42, -16)
Al resolver las ecuaciones (1) y (3), obtenemos
x = -6/11 y y = -24/11
Entonces las coordenadas de C son (-6/11, -24/11)
Ahora supongamos que P, Q y R son el punto medio del lado AB, BC y AC
Entonces, las coordenadas de los puntos medios son:
P = ((-2 -42)/2, (0 – 16)/2) = (-22, -8)
P = ((-42 – 6/11)/2, (-16 – 24/11)/2) = (-234/11, -100/11)
R = ((-2 -6/11)/2, (0 – 24/11)/2) = (-14/11, -12/11)
Ahora encontramos que la mediana de AP es
= y + 8/x + 22 =
= y + 8/x + 22 = -88 + 24/-242 + 6 = 16/59
= 16x – 59y + 352 – 572 = 0
= 16x – 59y – 120 = 0
De manera similar, la mediana de BQ es 25x – 53y + 50 = 0
Y la mediana de CR es 41x – 112y – 70 = 0
Pregunta 5. Demuestra que las líneas y = √3x + 1, y = 4 y y = -√3x + 2 forman un triángulo equilátero.
Solución:
Consideremos que ABC es un triángulo en el que A, B y C son los vértices del triángulo.
La ecuación de las rectas son:
y = √3x + 1 …..(1)
y = 4 …..(2)
y = -√3x + 2 …..(3)
Al resolver las ecuaciones (1) y (2), obtenemos
4 = √3x + 1
x = 4 – 1/√3 = 3/√3 = √3
Entonces, las coordenadas del punto A son (√3, 4)
Al resolver las ecuaciones (2) y (3), obtenemos
4 = -√3x + 2
√3x = -2
x = -2/√3
x = -2√3/3
Entonces, las coordenadas del punto B son (-2√3/3, 4)
Al resolver las ecuaciones (1) y (3), obtenemos
√3x + 1 = -√3x + 2
2√3x = 1
x = 1/2√3 = √3/6
y = √3(√3/6 + 1) = 3/2
Entonces, las coordenadas del punto C son (√3/6, 3/2)
Ahora tenemos,
AB =
= 5√3/3 unidades
antes de Cristo
C.A.
Aquí, AB = BC = AC
Por lo tanto, el triángulo ABC es equilátero
Pregunta 6 (i). Clasifica 2x + y – 1 = 0 y 3x + 2y + 5 = 0 como coincidentes, paralelas o intersecantes.
Solución:
Las ecuaciones de las rectas son:
2x + y – 1 = 0
3x + 2y + 5 = 0
Ahora, al escribir las ecuaciones anteriores en la forma y = mx + c
y = -2x + 1,
y = -3x/2 – 5/2
Entonces, la pendiente de ambas ecuaciones es
m1 = -2 y m2 = -3/2
Ahora
m1 ≠ m2 y m1m2 ≠ -1
Por lo tanto, las rectas se cortan
Pregunta 6(ii). Clasifica x – y = 0 y 3x – 3y + 5 = 0 como coincidentes, paralelas o intersecantes.
Solución:
Las ecuaciones de las rectas son:
x – y = 0
3x – 3y + 5 = 0
Ahora, al escribir las ecuaciones anteriores en la forma y = mx + c
y = x
y = x + 5/3
Entonces, la pendiente de ambas ecuaciones es
m1 = 1 y m2 = 1
Las pendientes de ambas rectas son iguales
Por lo tanto, las rectas son paralelas.
Pregunta 6 (iii). Clasifica 3x + 2y – 4 = 0 y 6x + 4y – 8 = 0 como coincidentes, paralelos o intersecantes.
Solución:
Las ecuaciones de las rectas son:
3x + 2y – 4 = 0
6x + 4y – 8 = 0
Ahora, al escribir las ecuaciones anteriores en la forma y = mx + c
y = -3x/2 + 2
y = -3x/2 + 2
Entonces, la pendiente de ambas ecuaciones es
m1 = -3/2 y m2 = -3/2
Entonces, m1= m2 = -3/2
Por lo tanto, las rectas son coincidentes.
Pregunta 7. Encuentra la ecuación de la unión del punto (3, 5) al punto de intersección de las rectas 4x + y – 1 = 0 y 7x – 3y – 35 = 0.
Solución:
Dada la ecuación de las rectas son
4x + y – 1 = 0 …..(1)
7x – 3y – 35 = 0 …..(2)
De la ecuación (1), obtenemos
y = 1 – 4x
Ahora pon el valor de y en la ecuación (2), obtenemos
7x – 3(1 – 4x) – 35 = 0
7x – 3 + 12x – 35 = 0
19x = 38
x = 2
y = 1 – 4x = 1 – 8 = -7
Ahora tenemos que encontrar la ecuación de la recta que une el punto P(2, -7) y Q(3, 5)
La ecuación de la línea PQ es
y – y 1 = m(x – x 1 )
y-y1 = (
x- x1 )
y – (-7) =
y + 7 = 12(x – 2)
y-12x = -31
12x-y-31 = 0
Por lo tanto, la ecuación de la recta es 12x – y – 31 = 0
Pregunta 8. Encuentra la ecuación de la línea que pasa por el punto de intersección de las líneas 4x – 7y – 3 = 0 y 3x – 3y + 1 = 0 que tiene intersecciones iguales en los ejes.
Solución:
Dada la ecuación de las rectas son
4x – 7y = 3
2x – 3y = -1
Al resolver las ecuaciones anteriores, obtenemos el punto de intersección,
x = -B, y = -5
Ahora, el punto de intersección de las rectas dadas es (-8, -5) ecuación
de línea que hace intersecciones iguales (a) en los ejes de coordenadas es,
x + y = un
-8 – 5 = un
a = -13
Por lo tanto, la ecuación de la línea es x + y = -13
Pregunta 9. Demuestre que el área del triángulo formado por las rectas y = m 1 x, y = m 2 x, y y = c es igual a c 2 /4(√33 + √11), donde m 1 , m 2 son las raíces de la ecuación x 2 + (√3 + 2)x + √3 – 1 = 0.
Solución:
Dada la ecuación de las rectas son
y = metro 1 x …..(1)
y = metro 2 x …..(2)
y = c …..(3)
Al resolver la ecuación (1) y (2), obtenemos A(0, 0)
Al resolver las ecuaciones (1) y (3), obtenemos A(c/m 1 , c)
Al resolver las ecuaciones (2) y (3), obtenemos A(c/m 2 , c)
Ahora encontramos el área del triángulo cuando se dan tres vértices es
= 1/2(x 2 (y 2 – y 3 ) + x 2 (y 3 – y 1 ) + x 3 (y 1 – y 2 ))
Dado que m 1 y m 2 son raíces de x 2 + (√3 + 2)x + √3 – 1 = 0
Producto de raíces = m 1 m 2 = √3 – 1
|m 2 -m 1 |=
|m 2 -m 1 |=
Área =
Al racionalizar el denominador, obtenemos
Por lo tanto probado
Pregunta 10. Si la línea recta 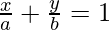 pasa por el punto de intersección de las líneas x + y = 3 y 2x – 3y = 1 y es paralela a x – y – 6 = 0, encuentra a y b.
pasa por el punto de intersección de las líneas x + y = 3 y 2x – 3y = 1 y es paralela a x – y – 6 = 0, encuentra a y b.
Solución:
Dada la ecuación de las rectas son
x + y = 3
2x – 3y = 1
Al resolver ambas ecuaciones obtenemos el punto de intersección (2, 1)
Se da que la recta x/a + y/b = 1 es paralela a la recta x – y – 6 = 0
entonces, la pendiente = 1
Ahora encontramos la ecuación de la recta que pasa por (2, 1) y tiene pendiente = 1 es
y – y 1 = m(x – x 1 )
y-1 = 1(x-2)
y-1 = x-2
y – x = -2 + 1
y – x = -1
x – y = 1
Al comparar con x/a + y/b = 1, obtenemos
a = 1, b = -1
Publicación traducida automáticamente
Artículo escrito por ysachin2314 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA