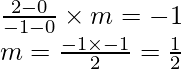Clase 11 RD Sharma Solutions – Capítulo 23 Las Líneas Rectas- Ejercicio 23.12

Pregunta 11. Halla la ecuación de la bisectriz derecha del segmento de recta que une los puntos (a, b) y (a ₁ , b ₁ ).

Solución:

Consideremos que P(a, b) y Q(a ₁ , b ₁ ) son los puntos dados y O el punto medio de la recta PQ.

Entonces la coordenada O = ((a + a ₁ )/, (b + b ₁ )/2)

Pendiente de la línea PQ = $\frac{b_1-b}{a_1-a}$

Y la pendiente de la bisectriz derecha de AB(m’) = $-\frac{a_1-a}{b_1-b}$

La ecuación de la línea requerida es

y – y ₁ = m'(x – x ₁ )

$y-(\frac{b+b_1}{2})=\frac{a-a_1}{b-b_1}(x-\frac{a+a_1}{2})$

2x(a ₁ – a) + 2y(b ₁ – b) + a ² + b ² = a ₁² + b ₁²

2x(a ₁ – a) + 2y(b ₁ – b) + (a ² + b ² )– (a ₁² + b ₁² ) = 0

2x(a ₁ – a) + 2y(b ₁ – b) + (a ² + b ² )– (a ₁² + b ₁² ) = 0

Pregunta 12. Encuentra la imagen del punto (2, 1) con respecto a la línea espejo x + y – 5 = 0.

Solución:

Consideremos que P(2, 1) es la imagen de Q(a, b) son los puntos dados y O el punto medio de la recta PQ.

Entonces la coordenada O = ((2 + a)/2, (1 + b)/2)

Y el punto O se encuentra en la línea x + y – 5 = 0

(2 + a)/2 + (1 + b)/2 – 5 = 0

a + b = 7 ………(1)

Aquí, x + y – 5 = 0 es perpendicular a PQ

Entonces, (pendiente de PQ) x (pendiente de AB) = -1

$-1\times (\frac{b-1}{a-2})=-1$

segundo – 1 = un – 2

b – a = -1 ………(2)

Al resolver las ecuaciones (1) y (2), obtenemos

a = 5 y b = 2

Por lo tanto, la imagen de (1, 2) en x + y – 5 = 0 es (4, 3)

Pregunta 13. Si la imagen del punto (2, 1) con respecto a la línea espejo es (5, 2), encuentra la ecuación del espejo.

Solución:

Consideremos que A(5, 2) es imagen de B(2, -1) y O es el punto medio de AB

Entonces la coordenada O = (7/2, 3/2)

Consideremos PQ como el espejo y la recta AB perpendicular a PQ

Entonces, (pendiente de PQ) x (pendiente de AB) = -1

(2 – 1/5 – 2) x (pendiente de AB) = -1

(pendiente de AB) = -3

Entonces la ecuación del espejo es

y-3/2 = -3(x-7/2)

2y – 3 = -6x + 21

3x + y – 12 = 0

Pregunta 14. Encuentra la ecuación de la recta paralela a 3x – 4y + 6 = 0 y que pasa por el punto medio de los puntos de unión (2, 3) y (4, -1).

Solución:

Se da que A(2, 3) y B(4, -1) y O son el punto medio de AB

Entonces la coordenada O = (3, 1)

Se da que la ecuación de la recta paralela a 3x – 4y + 6 = 0

Asi que,

y = 3x/4 + 3/2

Al comparar y = mx + c, obtenemos

metro = 3/4

Ahora pon el valor de m y (x ₁ , y ₁ ) es eq(1), obtenemos

La ecuación requerida de la línea es

y – y ₁ = m(x – x ₁ )

y-1 = 3/4(x-3)

4y – 4 = 3x – 9

3x – 4y = 5

3x – 4y = 5

Pregunta 15. Demuestra que las rectas 2x – 3y + 1 = 0, x + y = 3, 2x – 3y = 2 y x + y = 4 forman un paralelogramo.

Solución:

Como sabemos que en un paralelogramo los lados opuestos son paralelos y los lados paralelos tienen igual pendiente.

Entonces, la pendiente de la línea 2x – 3y + 1 = 0

m ₁ = 2/3 …….(1)

La pendiente de la línea x + y = 3

m2 ₌ -1 …….(2)

La pendiente de la recta 2x – 3y – 2 = 0

m ₃ = 2/3 …….(3)

La pendiente de la recta x + y = 4

m ₄ = -1 …….(4)

De (1), (2), (3) y (4), obtenemos

Concluimos que los lados opuestos de ABCD tienen la misma pendiente

Por lo tanto, el cuadrilátero dado es un paralelogramo.

Pregunta 16. Encuentra la ecuación de una línea trazada perpendicularmente a la línea x/4 + y/6 = 1 a través del punto donde se encuentra con el eje y.

Solución:

Consideremos que la ecuación requerida de la línea es

y – y ₁ = m(x – x ₁ ) ……….(1)

La línea requerida es perpendicular a la línea dada x/4 + y/6 = 1

Cuando x = 0

y/6 = 1

y = 6

Entonces, el punto (x ₁ , y ₁ ) es (0, 6)

Se da que la ecuación de línea requerida es perpendicular a la línea x/4 + y/6 = 1

Asi que,

(pendiente de la línea requerida) x (pendiente de la línea dada) = -1

m1 = -1/(-6/4) = 4/6 = 2/3

₁₁

2x – 3y = -18

2x – 3y + 18 = 0

2x – 3y + 18 = 0

Pregunta 17. La perpendicular desde el origen a la recta y = mx + c la corta en el punto (-1, 2). Encuentre los valores de m y c.

Solución:

Consideremos el punto O (0, 0) y P (-1, 2) y OP es perpendicular a la recta dada y = mx + c

Entonces, (pendiente de OP) x (pendiente de línea)=-1

$\frac{2-0}{-1-0}\times m=-1\\ m=\frac{-1\times -1}{2}=\frac{1}{2}$

Y el punto P se encuentra en la línea $y=\frac{1}{2}+c$ entonces,

2 = (1/2)(-1) + c

c = 2 + 1/2 = 5/2

Por lo tanto, el valor de c = 5/2 y m = 1/2

Pregunta 18. Encuentra la ecuación de la bisectriz derecha del segmento de línea que une los puntos (3, 4) y (-1, 2).

Solución:

Consideremos que P(3, 4) y Q(-1, 2) son el punto dado y O el punto medio de AB

Entonces, la coordenada O = (1, 3)

Y la pendiente de la recta PQ es $\frac{2-4}{-1-3}=\frac{-2}{-4}=\frac{1}{2}$

La bisectriz derecha de PQ es -2

La ecuación de la línea requerida es

y-3 = (-2)(x-1)

y-3 = -2x + 2

2x + y – 5 = 0

Por lo tanto, la ecuación requerida de la línea es 2x + y – 5 = 0

Pregunta 19. La recta que pasa por (h, 3) y (4, 1) se cruza con la recta 7x – 9y – 19 = 0 en ángulo recto. Encuentre el valor de h.

Solución:

Consideremos que P (h, 3) y Q(4, 1) son los puntos dados

Ahora la pendiente de la recta 7x – 9y – 19 = 0 es 7/9

Se da que la recta PQ es perpendicular a 7x – 9y – 19 = 0

asi que

7/9 x (1 – 3)/(4 – h) = -1

9h = 22

h = 22/9

Por lo tanto, el valor de h es 22/9

Pregunta 20. Encuentra la imagen del punto (3, 8) con respecto a la recta x + 3y = 7 suponiendo que la recta sea un espejo plano.

Solución:

Consideremos A(5, 2) imagen de B(a, b) y O el punto medio de AB

Entonces, la coordenada de O = ((3 + a)/2, (8 + b)/2)

El punto O se encuentra en la línea x + 3y = 7

Entonces, (3 + a)/2 + 3 x ((8 + b)/2) = 7

a + 13b + 13 = 0 ……(1)

Se sabe que la recta AB es perpendicular al espejo PQ

Entonces, pendiente de AB x pendiente de PQ = -1

(b – 8/a – 3) x -1/3 = -1

3a – b – 1 = 0 ……(2)

Al resolver las ecuaciones (1) y (2), obtenemos

a = -1, b = -4

Por lo tanto, la imagen es (-1, -4)

Publicación traducida automáticamente

Artículo escrito por ysachin2314 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 11 RD Sharma Solutions – Capítulo 23 Las Líneas Rectas- Ejercicio 23.12 | conjunto 2

Pregunta 11. Halla la ecuación de la bisectriz derecha del segmento de recta que une los puntos (a, b) y (a ₁ , b ₁ ).

Pregunta 12. Encuentra la imagen del punto (2, 1) con respecto a la línea espejo x + y – 5 = 0.

Pregunta 13. Si la imagen del punto (2, 1) con respecto a la línea espejo es (5, 2), encuentra la ecuación del espejo.

Pregunta 14. Encuentra la ecuación de la recta paralela a 3x – 4y + 6 = 0 y que pasa por el punto medio de los puntos de unión (2, 3) y (4, -1).

Pregunta 15. Demuestra que las rectas 2x – 3y + 1 = 0, x + y = 3, 2x – 3y = 2 y x + y = 4 forman un paralelogramo.

Pregunta 16. Encuentra la ecuación de una línea trazada perpendicularmente a la línea x/4 + y/6 = 1 a través del punto donde se encuentra con el eje y.

Pregunta 17. La perpendicular desde el origen a la recta y = mx + c la corta en el punto (-1, 2). Encuentre los valores de m y c.

Pregunta 18. Encuentra la ecuación de la bisectriz derecha del segmento de línea que une los puntos (3, 4) y (-1, 2).

Pregunta 19. La recta que pasa por (h, 3) y (4, 1) se cruza con la recta 7x – 9y – 19 = 0 en ángulo recto. Encuentre el valor de h.

Pregunta 20. Encuentra la imagen del punto (3, 8) con respecto a la recta x + 3y = 7 suponiendo que la recta sea un espejo plano.

Deja una respuesta Cancelar la respuesta

Pregunta 11. Halla la ecuación de la bisectriz derecha del segmento de recta que une los puntos (a, b) y (a 1 , b 1 ).

Pregunta 12. Encuentra la imagen del punto (2, 1) con respecto a la línea espejo x + y – 5 = 0.

Pregunta 13. Si la imagen del punto (2, 1) con respecto a la línea espejo es (5, 2), encuentra la ecuación del espejo.

Pregunta 14. Encuentra la ecuación de la recta paralela a 3x – 4y + 6 = 0 y que pasa por el punto medio de los puntos de unión (2, 3) y (4, -1).

Pregunta 15. Demuestra que las rectas 2x – 3y + 1 = 0, x + y = 3, 2x – 3y = 2 y x + y = 4 forman un paralelogramo.

Pregunta 16. Encuentra la ecuación de una línea trazada perpendicularmente a la línea x/4 + y/6 = 1 a través del punto donde se encuentra con el eje y.

Pregunta 17. La perpendicular desde el origen a la recta y = mx + c la corta en el punto (-1, 2). Encuentre los valores de m y c.

Pregunta 18. Encuentra la ecuación de la bisectriz derecha del segmento de línea que une los puntos (3, 4) y (-1, 2).

Pregunta 19. La recta que pasa por (h, 3) y (4, 1) se cruza con la recta 7x – 9y – 19 = 0 en ángulo recto. Encuentre el valor de h.

Pregunta 20. Encuentra la imagen del punto (3, 8) con respecto a la recta x + 3y = 7 suponiendo que la recta sea un espejo plano.

Deja una respuesta Cancelar la respuesta

Pregunta 11. Halla la ecuación de la bisectriz derecha del segmento de recta que une los puntos (a, b) y (a ₁ , b ₁ ).