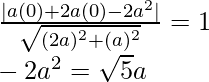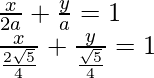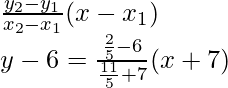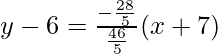Clase 11 RD Sharma Solutions – Capítulo 23 Las Líneas Rectas- Ejercicio 23.12

Pregunta 21. Encuentra las coordenadas del pie de la perpendicular desde el punto (-1, 3) hasta la línea 3x – 4y – 16 = 0.

Solución:

Consideremos el pie de la perpendicular de P(-1, 3) sobre la línea 3x – 4y = 16 sea Q(a, b)

Entonces, (pendiente de la línea dada) x (pendiente de PQ) = -1

$\frac{3}{4} \times \frac{b-3}{a+1}$

3(b – 3) = -4a – 4

3b – 9 = -4a – 4

4a + 3b = 5 …….(1)

Se da que Q(a, b) se encuentran en la recta 3x – 4y = 16

3a – 4b = 16 …….(2)

Al resolver las ecuaciones (1) y (2), obtenemos

a = (68/25) y b = (-49/25)

Por lo tanto, la coordenada de Q es (68/25, -49/25)

Pregunta 22. Halla la proyección del punto (1, 0) sobre la recta que une los puntos (-1, 2) y (5, 4).

Solución:

Consideremos que P(-1, 2) y Q(5, 4) son el punto dado

Entonces, la ecuación de la recta PQ es

y – y ₁ = m(x – x ₁ )

$y-2=\frac{4-2}{5+1}(x+1)\\ y-2=\frac{2}{6}(x+1)$

3y – x = 7 ……..(1)

Y la pendiente de la recta PQ = 1/3

Consideremos que el punto A(1, 0) es el punto dado y B(x ₁ , y ₁ ) la proyección de A

Entonces, la pendiente de AB = -3

La ecuación de PQ es

y-0 = -3(x-1)

y = -3x + 3 …….(2)

Al resolver las ecuaciones (1) y (2), obtenemos

$3y-(\frac{y-3}{-3})=7$

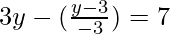
-9y – y + 3 = -21

-10 años = -24

y = 12/5

12/5 = -3x + 3

-3x = 12/5 – 3 = (12 -15)/5 = -3/5

X = 1/5

Por lo tanto, el B(1/5, 12/5)

Pregunta 23. Halla la ecuación de una recta perpendicular a la recta √3x – y + 5 = 0 ya una distancia de 3 unidades del origen.

Solución:

Consideremos que la ecuación requerida de la línea es

y – y ₁ = m'(x – x ₁ ) ……….(1)

Se da que la recta requerida es perpendicular a la recta √3x – y + 5 = 0

Entonces, la pendiente de la recta es

y = √3x + 5

Al comparar y = mx + c, obtenemos

metro = √3

m’ = -1/m = -1/√3

y el punto es (x ₁ , y ₁ ) = (3, 3)

₁₁

y-3= -1/√3 (x-3)

x + √3y – 6 = 0

Por lo tanto, la ecuación requerida de la línea es x + √3y – 6 = 0

Pregunta 24. La línea 2x + 3y = 12 se encuentra con el eje x en A y el eje y en B. La línea que pasa por (5, 5) perpendicular a AB se encuentra con el eje x y la línea AB en C y E respectivamente. Si O es el origen de coordenadas, encuentre el área de la figura OCEB.

Solución:

Se da que la línea 2x+3y=12 se encuentra con el eje x en A y el eje y en B

Entonces, A es 2x = 12 = x = 6

A es (6, 0)

B es 3y = 12

y = 4

B es (0, 4)

Se da que la recta que pasa por (5, 5) perpendicular a 2x + 3y = 12 tendrá pendiente = 3/2

y – y ₁ = m(x – x ₁ )

(y-5) = 3/2(x-5)

Y 2y – 3x = -5 es la ecuación de la línea que se encuentra con el eje x en C y la línea en E

Entonces, C es -3x = -5

x = -5/3

E es (5/3, 0)

donde E es el punto de intersección de dos rectas

Entonces, 2x + 3y = 12

2y – 3x = -5

Ahora encontramos el área de OBCE = área de AOB – área de ACE

= 1/2 x AO x OB – 1/2 x CA x CE

= 24/2 – 1/2 x √13 x 2/3√13

= 24/2 – 1/2 x 2/3 x 13

= 12 – 13/3

= 23/3 unidad cuadrada

Pregunta 25. Encuentra la ecuación de la línea recta que corta las intersecciones en el eje x el doble que en el eje y y está a una unidad de distancia del origen.

Solución:

Consideremos que la ecuación de la línea en forma de intersección es $\frac{x}{a}+\frac{y}{b}=1$

Se da b que intercepta en el eje y = 2a

Entonces, la ecuación es

$\frac{x}{2a}+\frac{y}{a}=1$

hacha + 2ay = 2a ² ……..(1)

Ahora, a la distancia perpendicular de la ecuación (1) desde el origen se le da la unidad

Asi que, $\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}=1$

a = a, b = 2a, c = -2a ² , x ₁ = 0, y ₁ = 0

$\frac{|a(0)+2a(0)-2a^2|}{\sqrt{(2a)^2+(a)^2}}=1\\ -2a^2=\sqrt{5}a$

4a ⁴ = un ² 5

un ² = 5/4

a = ±√5/4

Entonces, la forma de intersección de la línea recta es

$\frac{x}{2a}+\frac{y}{a}=1\\ \frac{x}{&pm;\frac{2\sqrt{5}}{4}}+\frac{y}{&pm;\frac{\sqrt{5}}{4}}=1$

x + 2y = ±√5

Por lo tanto, la ecuación requerida de la línea es x + 2y = ±√5

Pregunta 26. Las ecuaciones de la mediatriz de los lados AB y AC de un triángulo ABC x – y + 5 = 0 y x + 2y = 0 respectivamente. Si el punto A es (1, -2), encuentre la ecuación de la línea BC.

Solución:

Consideremos (x1, y1) y (x2, y2) las coordenadas de B y C.

Se da que la mediatriz de AB es x – y + 5 = 0

Entonces, su pendiente = 1

Las coordenadas de F $=(\frac{x_1+1}{2},\frac{y_1-2}{2})$

De la figura se da que F se encuentra en x – y + 5 = 0

$\frac{x_1+1}{2}-\frac{y_1-2}{2}+5=0$

x ₁ + 1 – y ₁ + 2 + 10 = 0

x ₁ – y ₁ + 13 = 0 ……(1)

De la figura se da que AB es perpendicular a HF

Entonces, (pendiente de AB) x (pendiente de HF) = -1

$(\frac{y_1+2}{x_1-1})(1)=-1$

x ₁ + y ₁ + 1 = 0

Ahora al resolver la ecuación (1) y (2), obtenemos

x1 = -7, _y1 = ₆

Entonces, B es (-7, 6)

Ahora, la mediatriz de AC es x + 2y = 0

Entonces, su pendiente = -1/2

La coordenada de E $=(\frac{x_2+1}{2},\frac{y_2-2}{2})$

De la figura se da que E se encuentra en la bisectriz perpendicular de AC

$(\frac{x_2+1}{2})+2(\frac{y_2-2}{2})=0$

x2 + 1 + 2y ₂_– 4 = 0

x ₂ + 2y ₂ – 3 = 0 ……(3)

Además, AC es perpendicular a HE.

Entonces, (pendiente de AC) x (pendiente de HE) = -1

$(\frac{y_2+2}{x_2-1})(-\frac{1}{2})=-1$

y ₂ + 2 = 2x ₂ – 2

2x ₂ – y ₂ = 4 …..(4)

Al resolver la ecuación (3) y (4), obtenemos

x2 = 11/5, _y2₌ 2/5

Por lo tanto, el punto C es (11/5, 2/5)

Entonces, la ecuación de BC es

y – y ₁ = $\frac{y_2-y_1}{x_2-x_1}(x-x_1)\\ y-6=\frac{\frac{2}{5}-6}{\frac{11}{5}+7}(x+7)$

$y-6=\frac{-\frac{28}{5}}{\frac{46}{5}}(x+7)$

y-6 = -14/23(x + 7)

23y – 138 = -14x – 98

14x + 23y – 40 = 0

Por lo tanto, la ecuación requerida de la línea es 14x + 23y – 40 = 0

Pregunta 27. Halla la ecuación de la recta que pasa por el punto de intersección de las rectas 5x – 6y -1 = 0 y perpendicular a la recta 3x – 5y + 11 = 0.

Solución:

Consideremos que M es el punto de intersección de las rectas dadas 5x – 6y – 1 = 0 y 3x + 2y + 5 = 0

Al resolver ambas ecuaciones obtenemos el punto de intersección como M (-1, -1).

Ahora encontramos la pendiente de 3x – 5y + 11 = 0

5y = 3x + 11

y = 3x/5 + 11/5

metro = 3/5

De la figura podemos ver que AP es perpendicular a la línea 3x – 5y + 11 = 0

Entonces, la pendiente de AP = -5/3

Ahora la ecuación de AP es

y – y ₁ = m(x – x ₁ )

y + 1 = -5/3(x + 1)

3y + 3 = -5x – 5

5x + 3y + 8 = 0

Por tanto, la ecuación de la recta AP es 5x + 3y + 8 = 0

Publicación traducida automáticamente

Artículo escrito por ysachin2314 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 11 RD Sharma Solutions – Capítulo 23 Las Líneas Rectas- Ejercicio 23.12 | conjunto 3

Pregunta 21. Encuentra las coordenadas del pie de la perpendicular desde el punto (-1, 3) hasta la línea 3x – 4y – 16 = 0.

Pregunta 22. Halla la proyección del punto (1, 0) sobre la recta que une los puntos (-1, 2) y (5, 4).

Pregunta 23. Halla la ecuación de una recta perpendicular a la recta √3x – y + 5 = 0 ya una distancia de 3 unidades del origen.

Pregunta 24. La línea 2x + 3y = 12 se encuentra con el eje x en A y el eje y en B. La línea que pasa por (5, 5) perpendicular a AB se encuentra con el eje x y la línea AB en C y E respectivamente. Si O es el origen de coordenadas, encuentre el área de la figura OCEB.

Pregunta 25. Encuentra la ecuación de la línea recta que corta las intersecciones en el eje x el doble que en el eje y y está a una unidad de distancia del origen.

Pregunta 26. Las ecuaciones de la mediatriz de los lados AB y AC de un triángulo ABC x – y + 5 = 0 y x + 2y = 0 respectivamente. Si el punto A es (1, -2), encuentre la ecuación de la línea BC.

Pregunta 27. Halla la ecuación de la recta que pasa por el punto de intersección de las rectas 5x – 6y -1 = 0 y perpendicular a la recta 3x – 5y + 11 = 0.

Deja una respuesta Cancelar la respuesta