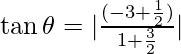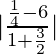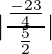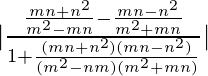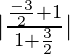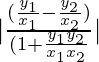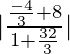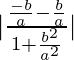Pregunta 1: Encuentra los ángulos entre cada uno de los siguientes pares de líneas rectas.
(yo) 3x+y+12=0 y x+2y-1=0
Solución:
Las ecuaciones dadas de las rectas son,3x + y + 12 = 0, x + 2y -1 = 0
Sean m 1 ym 2 las pendientes de estas rectas respectivamente.
Por y = mx +c, obtenemos m 1 =-3 y m 2 =-1/2
Sea θ el ángulo entre las dos rectas,
Mediante el uso de la fórmula
⇒
⇒ 1
Por lo tanto,
Los ángulos entre las dos líneas es de 45° .
(ii) 3x-y+5 = 0 y x-3y+1 = 0
Solución:
Las ecuaciones dadas de las rectas son 3x – y + 5 = 0, x – 3y +1 = 0
Sean m 1 y m 2 las pendientes de estas rectas respectivamente.
Por y = mx +c, obtenemos m 1 =3 y m 2 =1/3
Sea θ el ángulo entre las dos rectas,
Lo sabemos,
⇒
Por lo tanto,
El ángulo entre las dos rectas es
(iii) 3x+4y -7 = 0 y 4x-3y+5 = 0
Solución:
Las ecuaciones dadas de las rectas son 3x + 4y – 7 = 0, 4x – 3y+5 = 0
Sean m 1 ym 2 las pendientes de estas rectas respectivamente.
Por y= mx +c, obtenemos m 1 =
y m 2 =
Aquí, si observamos cuidadosamente, m 1 m 2 = -1 , lo que significa
A partir de la fórmula ,
el denominador se convertirá en 0,
Por lo tanto
,
El ángulo entre las dos líneas es de 90°.
(iv) x-4y = 3 y 6x-y = 11
Solución:
Las ecuaciones dadas de las líneas son x – 4y =3, 6x – y =11
Sean m 1 ym 2 las pendientes de estas rectas respectivamente.
Por y = mx +c, obtenemos , m 1 = 1/4 y m 2 = 6
Sea θ el ángulo entre las dos rectas,
Lo sabemos,
⇒
⇒
⇒
Por lo tanto,
El ángulo entre las dos rectas es
(v) (m 2 -mn)y = (mn+n 2 )x + n 3 y (mn+m 2 )y = (mn-n 2 )x + m 3
Solución:
Dadas dos rectas, sean m 1 ym 2 las pendientes de estas rectas.
Por y = mx +c, obtenemos m 1 =
y m 2 =
Sea θ el ángulo entre dos rectas,
Lo sabemos
⇒
⇒
⇒
Por lo tanto, el ángulo entre dos rectas es
.
Pregunta 2: Encuentra el ángulo agudo entre las líneas 2x-y+3 = 0 y x+y+2 = 0
Solución:
Sean m 1 ym 2 las pendientes de estas dos rectas
Por y = mx +c, obtenemos m 1 =2 y m 2 =-1
Sea θ el ángulo entre las dos rectas,
Lo sabemos,
⇒
⇒
Aquí necesitamos un ángulo agudo,
es positivo si el ángulo es agudo y negativo si es obtuso.
Por lo tanto,
.
El ángulo agudo entre las dos rectas es
.
Pregunta 3: Demuestra que los puntos (2, -1), (0, 2), (2, 3) y (4, 0) son las coordenadas de los vértices de un paralelogramo y encuentra el ángulo entre sus diagonales.
Solución:
Sean los puntos dados A = (2,-1), B = (0, 2), C = (2, 3) y D = (4, 0) son coordenadas de un paralelogramo.
Para que estos puntos formen un paralelogramo, es necesario que cualquier par de dos rectas formadas por estos puntos sean paralelas entre sí .
Entonces, ahora encontremos las pendientes de las líneas AB, BC, CD, DA usando la fórmula
Pendiente de línea
Pendiente de línea
Pendiente de línea
Pendiente de línea
Como las líneas AB son paralelas a CD y BC son paralelas a DA , los puntos forman un paralelogramo.
Ahora, Ángulo entre las diagonales del paralelogramo = Ángulo entre las rectas AC y BD.
Sean m 1 ym 2 las pendientes de estas rectas,
De la figura, el ángulo entre las diagonales
Lo sabemos
⇒
Por lo tanto, el ángulo entre las diagonales es
Pregunta 4: Encuentra los ángulos entre la línea que une los puntos (2, 0), (0, 3) y la línea x + y = 1.
Solución:
Sea la pendiente de la recta que une los puntos (2, 0) y (0, 3) m 1 = -3/2
pendiente de la recta m 2 =-1
Sea θ el ángulo entre las dos rectas,
Lo sabemos,
⇒
⇒
Por tanto, el ángulo agudo entre la recta y la recta que une los puntos es
Pregunta 5: Si θ es el ángulo que subtiende en el origen la recta que une los puntos (x1,y1)y (x2,y2), demostrar que 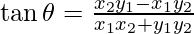 y
y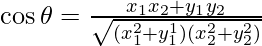
Solución:
Sean los puntos A = (x 1 , y 1 ), B = (x 2 , y 2 ) y origen O = (0, 0)
Las pendientes de las rectas que unen OA y OB son m 1 = y 1 /x 1 y m 2 = y 2 /x 2
Sea θ el ángulo entre las rectas OA y OB.
Lo sabemos,
⇒
Por lo tanto,
Por la fórmula
, obtenemos
Sustituyendo Tanθ de la ecuación anterior, obtenemos,
Por lo tanto, por lo tanto probado.
Pregunta 6: Demuestra que las rectas(a+ b)x+(a – b)y=2ab, (a – b)x+(a + b)y=2ab y x + y=0 forman un triángulo isósceles cuyo ángulo vertical es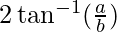
Solución:
Sean m1, m2, m3 las pendientes de las rectas dadas respectivamente.
metro 1 =
, metro 2 =
y metro 3 = -1
Sean θ 1 , θ 2 , θ 3 los ángulos entre las rectas
Ahora,
=
⇒
⇒
⇒
Sabemos que
, usando esta ecuación anterior
⇒
=
⇒
⇒
=
⇒
⇒
Aquí, el ángulo θ 2 y θ 3 son iguales, y θ 1 es el ángulo vertical
Por lo tanto, las líneas dadas forman un triángulo isósceles con ángulo vertical
Pregunta 7: Encuentra el ángulo entre las líneas x = a, por + c = 0
Solución:
Las líneas dadas tienen la forma de x = constante y y = constante respectivamente
donde x=c y y= -c/b
x = la línea c es paralela al eje y ya que no hay coeficiente y
y
es paralelo al eje x ya que no hay coeficiente x
Por lo tanto, el ángulo entre las dos líneas es de 90°
Pregunta 8: Encuentra la tangente del ángulo entre las líneas que tienen intersecciones 3, 4 y 1, 8 en los ejes respectivamente.
Solución:
La ecuación de la línea que tiene intersecciones a, b en los ejes x e y es
Por lo tanto, la recta con intersecciones 3,4 es
y la línea con intersecciones 1, 8 es
sean 1 y m 2 las pendientes de estas rectas,
m 1 =
y m 2 = -8
Ahora, sea θ el ángulo entre las rectas,
⇒
⇒
⇒
Por lo tanto, la tangente del ángulo entre las rectas es 4/7
Pregunta 9: Muestre que la línea a 2 x+ay+1 = 0 es perpendicular a la línea x-ay = 1
Solución:
Sean m 1 ym 2 las pendientes de las rectas dadas,m 1 =-a ym 2 =1/a
Aquí, si observamos cuidadosamente,m 1 m 2 =-1, lo que significa
De la fórmula
, el denominador se convertirá en 0 ,
Por lo tanto,
,
.
El ángulo entre las dos líneas es de 90° y son perpendiculares entre sí.
Por lo tanto, Por lo tanto probado.
Pregunta 10: Muestre que la tangente de un ángulo entre las rectas 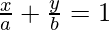 y
y 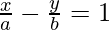 es
es 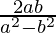 .
.
Solución:
Líneas dadas,
⇒
⇒
Sean las pendientes de estas rectas m 1 ym 2 respectivamente.
y
Ahora, sea θ el ángulo entre las rectas,
⇒
⇒
Por lo tanto, la tangente del ángulo entre las rectas es
Por lo tanto, probado.
Publicación traducida automáticamente
Artículo escrito por srinivasteja18 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA