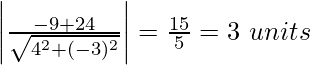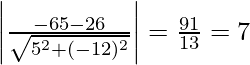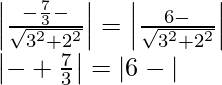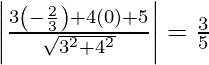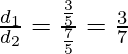Clase 11 RD Sharma Solutions- Capítulo 23 Las Líneas Rectas- Ejercicio 23.16

Pregunta 1. Determine la distancia entre el siguiente par de líneas paralelas:

(i) 4x – 3y – 9 = 0 y 4x – 3y – 24 = 0

(ii) 8x + 15y – 34 = 0 y 8x + 15y + 31 = 0

(iii) y = mx + c y y = mx + d

(iv) 4x + 3y – 11 = 0 y 8x + 6y = 15

Solución:

(i) 4x – 3y – 9 = 0 y 4x – 3y – 24 = 0

Dado:

Las rectas paralelas son

4x − 3y − 9 = 0 —(Ecuación-1)

4x − 3y − 24 = 0 —(Ecuación-2)

Sea ‘d’ la distancia entre las líneas dadas.

De este modo,

re = $\left|\frac{-9+24}{\sqrt{4^2+(-3)^2}}\right|=\frac{15}{5}=3\ units$

Por lo tanto,

La distancia entre las líneas paralelas dadas es de 3 unidades.

(ii) 8x + 15y – 34 = 0 y 8x + 15y + 31 = 0

Dado:

Las rectas paralelas son

8x + 15y − 34 = 0 —(Ecuación-1)

8x + 15y + 31 = 0 —(Ecuación-2)

Sea ‘d’ la distancia entre las líneas dadas.

De este modo,

re = $\left|\frac{-34-31}{\sqrt{8^2+15^2}}\right|=\frac{65}{17}\ units$

Por lo tanto,

La distancia entre líneas paralelas dadas es $\frac{65}{17}$ unidades.

(iii) y = mx + c y y = mx + d

La distancia entre y = mx + c y y = mx + d es

$\left|\frac{c-d}{\sqrt{m^2+1}}\right|$

(iv) 4x + 3y – 11 = 0 y 8x + 6y = 15

La distancia entre 4x + 3y – 11 = 0 y 8x + 6y = 15 es

$\left|\frac{-11-15}{\sqrt{4^2+3^2}}\right|=\frac{7}{10}\ units$

Pregunta 2. Las ecuaciones de dos lados de un cuadrado son 5x – 12y – 65 = 0 y 5x – 12y + 26 = 0. Encuentra el área del cuadrado.

Solución:

Dado:

Dos lados del cuadrado son 5x – 12y – 65 = 0 y 5x – 12y + 26 = 0

Los lados de un cuadrado son

5x − 12y − 65 = 0 —(Ecuación-1)

5x − 12y + 26 = 0 —(Ecuación-2)

Aquí podemos ver que las rectas (1) y (2) son paralelas.

Por lo tanto, la distancia entre ellos dará la longitud del lado del cuadrado.

Sea ‘d’ la distancia entre las líneas dadas.

re = $\left|\frac{-65-26}{\sqrt{5^2+(-12)^2}}\right|=\frac{91}{13}=7$

Por lo tanto,

Área del cuadrado = 7 ² = 49 unidades cuadradas

Pregunta 3. Encuentra la ecuación de dos rectas paralelas a x + 7y + 2 = 0 ya la unidad de distancia del punto (1, -1).

Solución:

Dado:

La ecuación es paralela a x + 7y + 2 = 0 y a la unidad de distancia del punto (1, -1)

La ecuación de la recta dada es

x + 7y + 2 = 0 —(Ecuación-1)

La ecuación de una línea paralela a la línea x + 7y + 2 = 0 se da a continuación:

x + 7y + λ = 0 —(Ecuación-2)

La recta x + 7y + λ = 0 está a una unidad de distancia del punto (1, − 1).

De este modo,

1 = $\left|\frac{1-7+λ}{\sqrt{1+49}}\right|$

λ – 6 = ± 5√2

λ = 6 + 5√2, 6 – 5√2

Ahora,

Sustituimos el valor de λ en la ecuación x + 7y + λ = 0, obtenemos

x + 7y + 6 + 5√2 = 0 y x + 7y + 6 – 5√2

Por lo tanto, las líneas requeridas:

x + 7y + 6 + 5√2 = 0 y x + 7y + 6 – 5√2

Pregunta 4. Demuestra que las rectas 2x + 3y = 19 y 2x + 3y + 7 = 0 son equidistantes de la recta 2x + 3y = 6.

Solución:

Dado:

Las rectas A, 2x + 3y = 19 y B, 2x + 3y + 7 = 0 también una recta C, 2x + 3y = 6.

Sea d ₁ la distancia entre las rectas 2x + 3y = 19 y 2x + 3y = 6,

Mientras que d ₂ es la distancia entre las líneas 2x + 3y + 7 = 0 y 2x + 3y = 6

re ₁ = $\left|\frac{-19-(-6)}{\sqrt{2^2+3^2}}\right|$ y re ₂ = $\left|\frac{7-(-6)}{\sqrt{2^2+3^2}}\right|$

re ₁ = $\left|-\frac{13}{\sqrt{13}}\right|=\sqrt{13}$ y re ₂ = $\left|\frac{13}{\sqrt{13}}\right|=\sqrt{13}$

Por tanto, probado, las rectas 2x + 3y = 19 y 2x + 3y + 7 = 0 son equidistantes de la recta 2x + 3y = 6

Pregunta 5. Encuentra la ecuación de la línea a mitad de camino entre las líneas paralelas 9x + 6y – 7 = 0 y 3x + 2y + 6 = 0.

Solución:

Dado:

9x + 6y – 7 = 0 y 3x + 2y + 6 = 0 son rectas paralelas

Las ecuaciones dadas de las líneas se muestran como:

3x + 2y – $\frac{7}{3}$ = 0 —(Ecuación-1)

3x + 2y + 6 = 0 —(Ecuación-2)

Sea la ecuación de la línea a medio camino entre las líneas paralelas (1) y (2)

3x + 2y + λ = 0 —(Ecuación-3)

La distancia entre (1) y (3) y la distancia entre (2) y (3) son iguales.

$\left|\frac{-\frac{7}{3}-λ}{\sqrt{3^2+2^2}}\right|=\left|\frac{6-λ}{\sqrt{3^2+2^2}}\right|\\ \left|-λ +\frac{7}{3}\right|=|6-λ |$

6 – λ = λ + $\frac{7}{3}$

λ = $\frac{11}{6}$

Ahora sustituimos el valor de λ en la ecuación 3x + 2y + λ = 0, obtenemos

3x + 2y + $\frac{11}{6}$ = 0

Tomando LCM

18x + 12y + 11 = 0

Por lo tanto,

La ecuación requerida de la línea es 18x + 12y + 11 = 0.

Pregunta 6. Encuentra la razón en la que la línea 3x + 4y + 2 = 0 divide la distancia entre las líneas 3x + 4y + 5 = 0 y 3x + 4y – 5 = 0.

Solución:

Claramente, la pendiente de cada una de las rectas dadas es igual a $-\frac{3}{4}$

Por tanto, la recta 3x + 4y + 2 = 0 es paralela a cada una de las rectas dadas.

Poniendo y = 0 en 3x + 4y + 2 = 0, obtenemos x = $-\frac{2}{3}$

Entonces, las coordenadas de un punto en 3x + 4y + 2 = 0 son \ $\left(-\frac{2}{3},0\right)$

La distancia d ₁ entre las rectas 3x + 4y + 2 = 0 y 3x + 4y + 5 = 0 viene dada por

d ₁ = $\left|\frac{3\left(-\frac{2}{3}\right)+4(0)+5}{\sqrt{3^2+4^2}}\right|=\frac{3}{5}$

La distancia d ₂ entre las rectas 3x + 4y + 2 = 0 y 3x + 4y – 5 =0 viene dada por

d ₂ = $\left|\frac{3\left(-\frac{2}{3}\right)+4(0)-5}{\sqrt{3^2+4^2}}\right|=\frac{7}{5}$

$\frac{d_1}{d_2}=\frac{\frac{3}{5}}{\frac{7}{5}}=\frac{3}{7}$

Entonces, 3x + 4y + 2 = 0 divide la distancia entre las líneas 3x + 4y + 5 = 0 y 3x + 4y – 5 = 0 en la razón 3 : 7.

Publicación traducida automáticamente

Artículo escrito por yashchuahan y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1. Determine la distancia entre el siguiente par de líneas paralelas:

Pregunta 2. Las ecuaciones de dos lados de un cuadrado son 5x – 12y – 65 = 0 y 5x – 12y + 26 = 0. Encuentra el área del cuadrado.

Pregunta 3. Encuentra la ecuación de dos rectas paralelas a x + 7y + 2 = 0 ya la unidad de distancia del punto (1, -1).

Pregunta 4. Demuestra que las rectas 2x + 3y = 19 y 2x + 3y + 7 = 0 son equidistantes de la recta 2x + 3y = 6.

Pregunta 5. Encuentra la ecuación de la línea a mitad de camino entre las líneas paralelas 9x + 6y – 7 = 0 y 3x + 2y + 6 = 0.

Pregunta 6. Encuentra la razón en la que la línea 3x + 4y + 2 = 0 divide la distancia entre las líneas 3x + 4y + 5 = 0 y 3x + 4y – 5 = 0.

Deja una respuesta Cancelar la respuesta