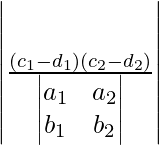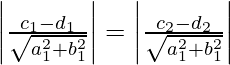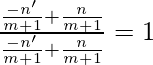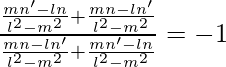Clase 11 RD Sharma Solutions- Capítulo 23 Las Líneas Rectas- Ejercicio 23.17

Pregunta 1. Demuestra que el área del paralelogramo formado por las líneas

a ₁ x + segundo ₁ y + c ₁ = 0, a ₁ x + segundo ₁ y + re ₁ = 0, a ₂ x + _{segundo 2} y + c ₂ = 0, a ₂ x + _{segundo 2} y + re ₂ = 0 son 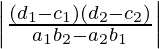$\left|\frac{(d_1-c_1)(d_2-c_2)}{a_1b_2-a_2b_1}\right|$ unidades cuadradas.

Deduce la condición para que estas rectas formen un rombo.

Solución:

Dado:

Las líneas dadas son

a ₁ x + b ₁ y + c ₁ = 0 —(ecuación-1)

a ₁ x + b ₁ y + d ₁ = 0 —(ecuación-2)

a ₂ x + b ₂ y + c ₂ = 0 —(ecuación-3)

a ₂ x + b ₂ y + d ₂ = 0 —(ecuación-4)

Probemos, el área del paralelogramo formado por las rectas a ₁ x + b ₁ y + c ₁ = 0, a ₁ x + b ₁ y + d ₁ = 0, a ₂ x + b ₂ y + c ₂ = 0, a ₂ x + b ₂ y + d ₂ = 0 es

$\left|\frac{(d_1-c_1)(d_2-c_2)}{a_1b_2-a_2b_1}\right|$ unidades cuadradas.

El área del paralelogramo formado por las rectas a ₁ x + b ₁ y + c ₁ = 0, a ₁ x + b ₁ y + d ₁ = 0, a ₂ x + b ₂ y + c ₂ = 0 y a ₂ x + b ₂ y + d ₂ = 0 se da a continuación:

Área = $\left|\frac{(c_1-d_1)(c_2-d_2)}{\begin{vmatrix}a_1&a_2\\b_1&b_2\end{vmatrix}}\right|$

Dado que \begin{vmatrix}a_1&a_2\\b_1&b_2\end{vmatrix} = a ₁ b ₂ – a ₂ b ₁

Por lo tanto, Área = $\left|\frac{(c_1-d_1)(c_2-d_2)}{a_1b_2-a_2b_1}\right|=\left|\frac{(d_1-c_1)(d_2-c_2)}{a_1b_2-a_2b_1}\right|$

Si el paralelogramo dado es un rombo, entonces la distancia entre el par de líneas paralelas es igual.

Por lo tanto, $\left|\frac{c_1-d_1}{\sqrt{a_1^2+b_1^2}}\right|=\left|\frac{c_2-d_2}{\sqrt{a_1^2+b_1^2}}\right|$

Por lo tanto probado.

Pregunta 2. Demuestra que el área del paralelogramo formado por las líneas 3x – 4y + a = 0, 3x – 4y + 3a = 0, 4x – 3y – a = 0 y 4x – 3y – 2a = 0 es 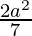$\frac{2a^2}{7}$ unidades cuadradas.

Solución:

Dado:

Las líneas dadas son

3x − 4y + a = 0 —(ecuación-1)

3x − 4y + 3a = 0 —(ecuación-2)

4x − 3y − a = 0 —(ecuación-3)

4x − 3y − 2a = 0 —(ecuación-4)

Tenemos que demostrar que el área del paralelogramo formado por las rectas 3x – 4y + a = 0, 3x – 4y + 3a = 0, 4x – 3y – a = 0 y 4x – 3y – 2a = 0 son $\frac{2a^2}{7}$ unidades cuadradas.

De la solución anterior, sabemos que

Área del paralelogramo = $\left|\frac{(c_1-d_1)(c_2-d_2)}{a_1b_2-a_2b_1}\right|$

Área del paralelogramo = $\left|\frac{(a-3a)(2a-a)}{(-9+16)}\right|=\frac{2a^2}{7}$ unidades cuadradas

Por lo tanto probado.

Pregunta 3. Demuestra que las diagonales del paralelogramo cuyos lados son lx + my + n = 0, lx + my + n’ = 0, mx + ly + n = 0 y mx + ly + n’ = 0 incluyen un ángulo π /2.

Solución:

Dado:

Las líneas dadas son

lx + my + n = 0 —(ecuación-1)

mx + ly + n’ = 0 —(ecuación-2)

lx + my + n’ = 0 —(ecuación-3)

mx + ly + n = 0 —(ecuación-4)

Tenemos que demostrar que las diagonales del paralelogramo cuyos lados son lx + my + n = 0, lx + my + n’ = 0, mx + ly + n = 0 y mx + ly + n’ = 0 incluyen un ángulo $\frac{\pi}{2}$ .

Resolviendo la ecuación (1) y (2), obtendremos

B = $\left(\frac{mn'-ln}{l^2-m^2}, \frac{mn-ln'}{l^2-m^2}\right)$

Resolviendo la ecuación (2) y (3), obtenemos

C = $\left(-\frac{n'}{m+1'}, -\frac{n'}{m+1}\right)$

Resolviendo la ecuación (3) y (4), obtenemos

re = $\left(\frac{mn-ln'}{l^2-m^2}, \frac{mn'-ln}{l^2-m^2}\right)$

Resolviendo la ecuación (1) y (4), obtenemos

un = $\left(-\frac{n}{m+1'}, -\frac{n}{m+1}\right)$

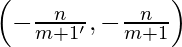
Sean m ₁ ym ₂ la pendiente de AC y BD.

Ahora,

metro ₁ = $\frac{\frac{-n'}{m+1}+\frac{n}{m+1}}{\frac{-n'}{m+1}+\frac{n}{m+1}}=1$

metro2 = _{_} $\frac{\frac{mn'-ln}{l^2-m^2}+\frac{mn-ln'}{l^2-m^2}}{\frac{mn-ln'}{l^2-m^2}+\frac{mn'-ln}{l^2-m^2}}=-1$

Por lo tanto,

metro ₁ metro ₂ = -1

Por lo tanto probado.

Publicación traducida automáticamente

Artículo escrito por yashchuahan y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1. Demuestra que el área del paralelogramo formado por las líneas

a 1 x + segundo 1 y + c 1 = 0, a 1 x + segundo 1 y + re 1 = 0, a 2 x + segundo 2 y + c 2 = 0, a 2 x + segundo 2 y + re 2 = 0 son unidades cuadradas.

Deduce la condición para que estas rectas formen un rombo.

Pregunta 2. Demuestra que el área del paralelogramo formado por las líneas 3x – 4y + a = 0, 3x – 4y + 3a = 0, 4x – 3y – a = 0 y 4x – 3y – 2a = 0 es unidades cuadradas.

Pregunta 3. Demuestra que las diagonales del paralelogramo cuyos lados son lx + my + n = 0, lx + my + n’ = 0, mx + ly + n = 0 y mx + ly + n’ = 0 incluyen un ángulo π /2.

Deja una respuesta Cancelar la respuesta

a ₁ x + segundo ₁ y + c ₁ = 0, a ₁ x + segundo ₁ y + re ₁ = 0, a ₂ x + _{segundo 2} y + c ₂ = 0, a ₂ x + _{segundo 2} y + re ₂ = 0 son $\left|\frac{(d_1-c_1)(d_2-c_2)}{a_1b_2-a_2b_1}\right|$ unidades cuadradas.

Pregunta 2. Demuestra que el área del paralelogramo formado por las líneas 3x – 4y + a = 0, 3x – 4y + 3a = 0, 4x – 3y – a = 0 y 4x – 3y – 2a = 0 es $\frac{2a^2}{7}$ unidades cuadradas.