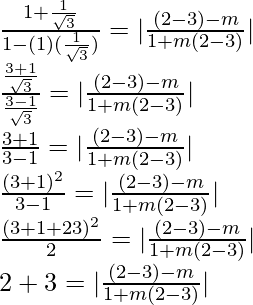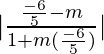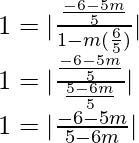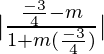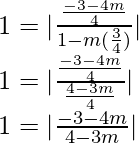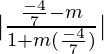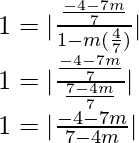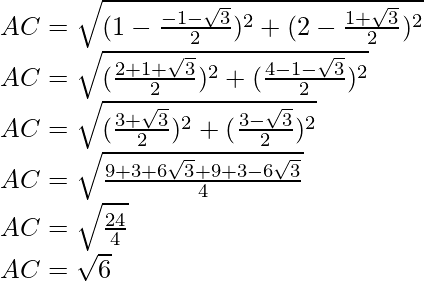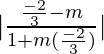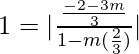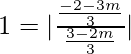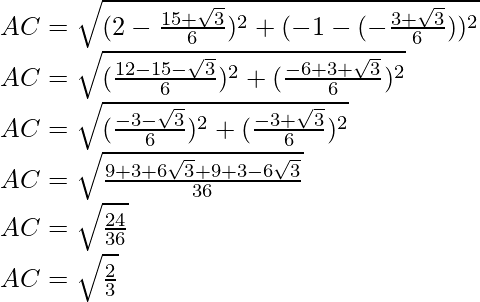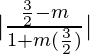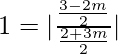Clase 11 RD Sharma Solutions – Capítulo 23 Las Líneas Rectas – Ejercicio 23.18

Pregunta 1: Encuentra la ecuación de las rectas que pasan por el origen y forman un ángulo de 45° con la recta √3x+y = 11.

Solución:

Como la línea 1 pasa por el origen, no habrá ningún intercepto, y tendrá la forma de y = mx (m como pendiente)

Para la línea 2: √3x+y = 11, la pendiente es M = -√3

Aquí, se da que estas dos líneas forman un ángulo de 45° entre ellas. Por eso,

Como sabemos, dos líneas que tienen pendientes como m y M tendrán un ángulo θ entre ellas de la siguiente manera:

$\mathbf{tan θ = |\frac{M-m}{1+mM}|}$

Aquí tenemos θ = 45°, m=m y M = -√3

bronceado 45° = $|\frac{-\sqrt{3}-m}{1+m(-\sqrt{3})}|$

1 = $|\frac{-\sqrt{3}-m}{1-\sqrt{3}m}|$

Tendremos dos casos,

1 = $\frac{-\sqrt{3}-m}{1-\sqrt{3}m}$ y 1 = $-\frac{-\sqrt{3}-m}{1-\sqrt{3}m}$

1-√3m = -√3-m y 1-√3m = √3+m

√3m-m = 1+√3 y √3m+m = 1-√3

m = $\frac{1+\sqrt{3}}{\sqrt{3}-1}$ y m = $\frac{1-\sqrt{3}}{\sqrt{3}+1}$

Racionalizando obtenemos

m = $\frac{(1+\sqrt{3})^2}{3-1}$ y m = $-\frac{(1-\sqrt{3})^2}{3-1}$

m = $\frac{1+3+2\sqrt{3}}{2}$ y m = $-\frac{1+3-2\sqrt{3}}{2}$

m = 2+√3 y m = -(2-√3)

m = √3+2 ym = √3-2

Por lo tanto, la ecuación de la línea será,

y = (√3+2)x y y = (√3-2)x

Pregunta 2: Encuentra la ecuación de las rectas que pasan por el origen y son inclinadas en un ángulo de 75° a la recta x+y+√3(yx)=a.

Solución:

Como la línea 1 pasa por el origen, no habrá ningún intercepto y tendrá la forma de y = mx (m como pendiente)

Para la línea 2: x+y+√3(yx)=a,

x+y+√3y-√3x=a

x(1-√3)+y(1+√3)=a

pendiente es M = $\frac{\sqrt{3}-1}{\sqrt{3}+1}$

Después de racionalizar, obtenemos

METRO = $\frac{(\sqrt{3}-1)^2}{3-1} = \frac{(3+1-2\sqrt{3})^2}{2}$ = 2-√3

Aquí, se da que estas dos líneas forman un ángulo de 75° entre ellas. Por eso,

Como sabemos, dos líneas que tienen pendientes como m y M tendrán un ángulo θ entre ellas de la siguiente manera:

$\mathbf{tan θ = |\frac{M-m}{1+mM}|}$

Aquí tenemos θ = 75°, m=m y M = 2-√3

tan 75° = $|\frac{(2-√3)-m}{1+m(2-√3)}|$

bronceado (45°+30°)= $|\frac{(2-√3)-m}{1+m(2-√3)}|$

Usando la identidad trigonométrica,

$tan (a+b) = \frac{tan \hspace{0.1cm}a + tan\hspace{0.1cm} b}{1-(tan\hspace{0.1cm} a) (tan\hspace{0.1cm} b)}$

$\frac{tan 45\degree + tan 30\degree}{1-(tan 45\degree) (tan 30\degree)} = |\frac{(2-\sqrt{3})-m}{1+m(2-\sqrt{3})}|$

$\frac{1 + \frac{1}{\sqrt{3}}}{1-(1) (\frac{1}{\sqrt{3}})} = |\frac{(2-√3)-m}{1+m(2-√3)}|\\ \frac{\frac{√3+1}{\sqrt{3}}}{\frac{√3-1}{\sqrt{3}}} = |\frac{(2-√3)-m}{1+m(2-√3)}|\\ \frac{√3+1}{√3-1} = |\frac{(2-√3)-m}{1+m(2-√3)}|\\ \frac{(√3+1)^2}{3-1} = |\frac{(2-√3)-m}{1+m(2-√3)}|\\ \frac{(3+1+2√3)^2}{2} = |\frac{(2-√3)-m}{1+m(2-√3)}|\\ 2+√3 = |\frac{(2-√3)-m}{1+m(2-√3)}|$

Tendremos dos casos,

2+√3 = $\frac{(2-\sqrt{3})-m}{1+m(2-\sqrt{3})}$ y 2+√3 = $-\frac{(2-\sqrt{3})-m}{1+m(2-\sqrt{3})}$

(2+√3)(1+m(2-√3)) = 2-√3-m y (2+√3)(1+m(2-√3)) = -(2-√3- metro)

(2+√3+m(2 ² -(√3) ² ) = 2-√3-m y (2+√3+m(2 ² -(√3) ² ) = √3-2+m

2+√3+m(4-3) = 2-√3-m y 2+√3+m(4-3) = √3-2+m

2+√3+m+m = 2-√3 y 2+√3+mm = √3-2

2m = -2-√3+2-√3 y 2+√3 = √3-2

2m = -2√3 y m no está definido

m = -√3 y m no está definido

Por lo tanto, la ecuación de la línea será,

y = -√3x y x = 0

Pregunta 3: Encuentra la ecuación de las rectas que pasan por (2,-1) y forman un ángulo de 45° con la recta 6x+5y-8=0.

Solución:

Como la línea 1 pasa por (2,-1), entonces tendrá la forma de

y-(-1) = m(x-2) (m como pendiente)

y+1 = m(x-2)

Para la línea 2: 6x+5y-8=0

5y = -6x + 8

$y = \frac{-6}{5}x + \frac{8}{5}$

pendiente es M = $\frac{-6}{5}$

Aquí, se da que estas dos líneas forman un ángulo de 45° entre ellas. Por eso,

Como sabemos, dos líneas que tienen pendientes como m y M tendrán un ángulo θ entre ellas de la siguiente manera:

$\mathbf{tan θ = |\frac{M-m}{1+mM}|}$

Aquí tenemos θ = 45°, m=m y M = $\frac{-6}{5}$

bronceado 45° = $|\frac{\frac{-6}{5}-m}{1+m(\frac{-6}{5})}|$

$1 = |\frac{\frac{-6-5m}{5}}{1-m(\frac{6}{5})}|\\ 1 = |\frac{\frac{-6-5m}{5}}{\frac{5-6m}{5}}|\\ 1 = |\frac{-6-5m}{5-6m}|$

Tendremos dos casos,

1 = $\frac{-6-5m}{5-6m}$ y 1 = $-\frac{-6-5m}{5-6m}$

5-6m = -6-5m y 5-6m = -(-6-5m)

6m-5m = 5+6 y 5-6m = 5m+6

m = 11 y 5m+6m = 5-6

m = 11 y m = $\frac{-1}{11}$

Por lo tanto, la ecuación de la línea será,

y+1 = 11(x-2) y y+1 = $\frac{-1}{11}(x-2)$

11x-y-23=0 y 11y+x+9 = 0

Pregunta 4: Encuentra la ecuación de las rectas que pasan por el punto (h,k) y están inclinadas en un ángulo tan ^-1 m con respecto a la recta y=mx+c.

Solución:

Como la línea 1 pasa por (h,k), entonces tendrá la forma de

y-(k) = M(xh) (M como pendiente)

Para la línea 2: y=mx+c (m como pendiente)

Aquí, se da que estas dos líneas forman un ángulo de tan ^-1 m entre ellas. Por eso,

Como sabemos, dos líneas que tienen pendientes como m y M tendrán un ángulo θ entre ellas de la siguiente manera:

$\mathbf{tan θ = |\frac{M-m}{1+mM}|}$

Aquí tenemos θ = tan ^-1 m,

tan (tan ^-1 m) = $|\frac{M-m}{1+mM}|$

$m = |\frac{M-m}{1+mM}|$

Tendremos dos casos,

m = $\frac{M-m}{1+mM}$ y m = $-\frac{M-m}{1+mM}$

m(1+mM) = Mm y m(1+mM) = -(Mm)

m+m ² M = Mm y m+m ² M = mM

2m = Mm ² M y m ² M = -M

M = $\frac{2m}{1-m^2}$ y M = 0

Por lo tanto, la ecuación de la línea será,

y-(k) = 0(xh) y yk = $\frac{2m}{1-m^2}(x-h)$

yk = 0 y (yk)(1-m ² ) = (2m)(xh)

Pregunta 5: Encuentra la ecuación de las rectas que pasan por el punto (2,3) e inclinadas 45° a la recta 3x+y-5=0.

Solución:

Como la línea 1 pasa por (2,3), entonces tendrá la forma de

y-3 = M(x-2) (M como pendiente)

Para la línea 2: 3x+y-5=0

y = -3x+5

pendiente m = -3

Aquí, se da que estas dos líneas forman un ángulo de 45° entre ellas. Por eso,

Como sabemos, dos líneas que tienen pendientes como m y M tendrán un ángulo θ entre ellas de la siguiente manera:

$\mathbf{tan θ = |\frac{M-m}{1+mM}|}$

Aquí, tenemos θ = 45°,

bronceado 45° = $|\frac{M-(-3)}{1+(-3)M}|$

$1 = |\frac{M+3}{1-3M}|$

Tendremos dos casos,

$1 = \frac{M+3}{1-3M}$ y $1 = -\frac{M+3}{1-3M}$

1-3M = M+3 y 1-3M = -(M+3)

M+3M = 1-3 y 1-3M = -M-3

4M = -2 y 3M-M = 1+3

M = $\frac{-2}{4}$ y 2M = 4

METRO = $\frac{-1}{2}$ y METRO = 2

Por lo tanto, la ecuación de la línea será,

$y-3 = \frac{-1}{2}(x-2)$ y y-3 = 2(x-2)

2y-6 = -(x-2) y y-3 = 2x-4

x+2y-8=0 y 2x-y-1=0

Pregunta 6: Hallar la ecuación de los lados de un triángulo rectángulo isósceles cuya ecuación de hipotenusa es 3x+4y=4 y el vértice opuesto es el punto (2,2).

Solución:

Como △ABC es un triángulo rectángulo isósceles en B.

∠A = ∠C = 45°

Podemos decir que AB y BC forman 45° con AC.

Sea la pendiente de AB como m ₁ y BC como m ₂ .

AB: (y-2) = m ₁ (x-2)

BC: (y-2) = m ₂ (x-2)

Pendiente de CA: 3x+4y=4

$y = \frac{-3}{4}x + 1$

La pendiente de AC es $\frac{-3}{4}.$

Aquí, se da que estas dos líneas forman un ángulo de 45° entre ellas. Por eso,

Como sabemos, dos líneas que tienen pendientes como m y M tendrán un ángulo θ entre ellas de la siguiente manera:

$\mathbf{tan θ = |\frac{M-m}{1+mM}|}$

Aquí, tenemos θ = 45°, y M = $\frac{-3}{4}$

bronceado 45° = $|\frac{\frac{-3}{4}-m}{1+m(\frac{-3}{4})}|$

$1 = |\frac{\frac{-3-4m}{4}}{1-m(\frac{3}{4})}|\\ 1 = |\frac{\frac{-3-4m}{4}}{\frac{4-3m}{4}}|\\ 1 = |\frac{-3-4m}{4-3m}|$

Tendremos dos casos,

1 = $\frac{-3-4m}{4-3m}$ y 1 = $-\frac{-3-4m}{4-3m}$

4-3 = -3-4 y 4-3 = -(-3-4)

4m-3 = -3-4 y 4-3 = 3+4

m = -7 y 4+3 = 4-3

m = -7 y m = $\frac{1}{7}$

Por lo tanto, la ecuación de las rectas será,

AB: (y-2) = m ₁ (x-2)

$y-2 = \frac{1}{7}(x-2)$

7y-x-12=0

BC: (y-2) = m ₂ (x-2)

y-2 = -7(x-2)

7x+y-16=0

Pregunta 7: La ecuación de un lado de un triángulo equilátero es xy=0 y un vértice es (2+√3,5). Demuestra que un segundo lado es y+(2-√3)x=6 y encuentra la ecuación del tercer lado.

Solución:

Como la ecuación de un lado del triángulo equilátero es xy=0 y un vértice es (2+√3,5),

Como, el punto (2+√3,5) no satisface xy=0. Entonces este es el vértice opuesto a la recta xy=0

En triángulo equilátero,

∠A = ∠B = ∠C = 60°

Podemos decir que AC y BC forman 60° con AB.

Sea la pendiente de AC como m ₁ y BC como m ₂ .

AB: (y-5) = metro ₁ (x-(2+√3))

BC: (y-5) = m ₂ (x-(2+√3))

Pendiente de CA: xy=0

y = x

La pendiente de AC es 1.

Aquí, se da que estas dos líneas forman un ángulo de 60° entre ellas. Por eso,

Como sabemos, dos líneas que tienen pendientes como m y M tendrán un ángulo θ entre ellas de la siguiente manera:

$\mathbf{tan θ = |\frac{M-m}{1+mM}|}$

Aquí tenemos θ = 60°, m = m ₁ y m ₂ y M = 1

bronceado 60° = $|\frac{1-m}{1+m(1)}|$

√3= $|\frac{1-m}{1+m}|$

Tendremos dos casos,

√3 = $\frac{1-m}{1+m}$ y √3 = $-\frac{1-m}{1+m}$

m = $\frac{1-\sqrt{3}}{1+\sqrt{3}}$ y √3(1+m) = -(1-m)

m = $\frac{1-\sqrt{3}}{1+\sqrt{3}}$ y √3+√3m = m-1

m = $\frac{1-\sqrt{3}}{1+\sqrt{3}}$ y √3m-m = -1-√3

m = $\frac{1-\sqrt{3}}{1+\sqrt{3}}$ y m = $\frac{1+\sqrt{3}}{1-\sqrt{3}}$

Después de racionalizar, obtenemos

m = $\frac{(1-\sqrt{3})^2}{1-3}$ y m = $\frac{(1+\sqrt{3})^2}{1-3}$

m = $\frac{1+3-2\sqrt{3}}{-2}$ y m = $\frac{1+3+2\sqrt{3}}{-2}$

m = -(2-√3) y m = -(2+√3)

Por lo tanto, la ecuación de las rectas será,

AB: (y-5) = metro ₁ (x-(2+√3))

y-5 = -(2-√3)(x-(2+√3))

y-5 = -(2-√3)x+ (2 ² -(√3) ² )

(2-√3)x+y-6 = 0

BC: (y-5) = m ₂ (x-(2+√3))

(y-5) = -(2+√3)(x-(2+√3))

y-5 = -(2+√3)x+(2+√3)^2

(2+√3)x+y-5 = 4+3+4√3

(2+√3)x+y = 12+4√3

Pregunta 8: Encuentra la ecuación de las dos rectas que pasan por (1,2) que forman dos lados de un cuadrado del cual 4x+7y=12 es una diagonal.

Solución:

Sea el punto opuesto a la diagonal 4x+7y=12 C(1,2)

Aquí, △BCD forman un triángulo rectángulo isósceles en C.

∠B = ∠D = 45°

Podemos decir que CD y BC forman 45° con BD.

Sea la pendiente de CD como m ₁ y BC como m ₂ .

CD: (y-2) = m ₁ (x-1)

BC: (y-2) = m ₂ (x-1)

Pendiente de BD : 4x+7y=12

$y = \frac{-4}{7}x + 3$

La pendiente de BD es $\frac{-4}{7}.$

Aquí, se da que estas dos líneas forman un ángulo de 45° entre ellas. Por eso,

Como sabemos, dos líneas que tienen pendientes como m y M tendrán un ángulo θ entre ellas de la siguiente manera:

$\mathbf{tan θ = |\frac{M-m}{1+mM}|}$

Aquí, tenemos θ = 45° y M = $\frac{-4}{7}$

bronceado 45° = $|\frac{\frac{-4}{7}-m}{1+m(\frac{-4}{7})}|$

$1 = |\frac{\frac{-4-7m}{7}}{1-m(\frac{4}{7})}|\\ 1 = |\frac{\frac{-4-7m}{7}}{\frac{7-4m}{7}}|\\ 1 = |\frac{-4-7m}{7-4m}|$

Tendremos dos casos,

1 = $\frac{-4-7m}{7-4m}$ y 1 = $-\frac{-4-7m}{7-4m}$

7-4m = -4-7m y 7-4m = -(-4-7m)

7m-4m = -4-7 y 7-4m = 4+7m

3m = -11 y 7m+4m = 7-4

m = $\frac{-11}{3}$ y 11m = 3

m = $\frac{-11}{3}$ y m = $\frac{3}{11}$

Por lo tanto, la ecuación de las rectas será,

CD: (y-2) = m ₁ (x-1)

$y-2 = \frac{-11}{3}(x-1)$

3y-6 = -11x+11

11x+3y-17=0

BC: (y-2) = m ₂ (x-1)

$y-2 = \frac{3}{11}(x-1)$

11y-22 = 3x-3

3x-11y+19=0

Pregunta 9: Encuentra la ecuación de las dos rectas que pasan por (1,2) y forman un ángulo de 60° con la recta x+y=0. Encuentra también el área del triángulo formado por las tres líneas.

Solución:

Como la ecuación de un lado del triángulo equilátero es x+y=0 y un vértice es (1,2),

Como, el punto (1,2) no satisface x+y=0. Entonces este es el vértice opuesto a la recta x+y=0

Por lo tanto, las líneas forman un triángulo equilátero,

∠A = ∠B = ∠C = 60°

Podemos decir que AC y BC forman 60° con AB.

Sea la pendiente de AC como m ₁ y BC como m ₂ .

AB: (y-2) = metro ₁ (x-1)

BC: (y-2) = m ₂ (x-1)

Pendiente de CA: x+y=0

y = -x

La pendiente de AC es -1.

Aquí, se da que estas dos líneas forman un ángulo de 60° entre ellas. Por eso,

Como sabemos, dos líneas que tienen pendientes como m y M tendrán un ángulo θ entre ellas de la siguiente manera:

$\mathbf{tan θ = |\frac{M-m}{1+mM}|}$

Aquí tenemos θ = 60° y M = -1

bronceado 60° = $|\frac{-1-m}{1+m(-1)}|$

√3= $|\frac{-1-m}{1-m}|$

Tendremos dos casos,

√3 = $\frac{-1-m}{1-m}$ y √3 = $-\frac{-1-m}{1-m}$

√3(1-m) = -1-m y √3(1-m) = 1+m

√3-√3m = -1-m y √3-√3m = m+1

√3m-m = √3+1 y +√3m+m = √3-1

m = $\frac{\sqrt{3}+1}{\sqrt{3}-1}$ y m = $\frac{\sqrt{3}-1}{\sqrt{3}+1}$

Después de racionalizar, obtenemos

m = $\frac{(\sqrt{3}+1)^2}{3-1}$ y m = $\frac{(\sqrt{3}-1)^2}{3-1}$

m = $\frac{1+3+2\sqrt{3}}{2}$ y m = $\frac{1+3-2\sqrt{3}}{2}$

m = 2+√3 y m = 2-√3

Por lo tanto, la ecuación de las rectas será,

AB: (y-2) = (2+√3)(x-1)

y-2=(2+√3)x-2-√3

(2+√3)xy-√3=0 ……………….(yo)

BC: (y-2) = (2-√3)(x-1)

y-2=(2-√3)x-2+√3

(2-√3)x-y+√3=0 ……………….(ii)

Usando (i) y x+y=0, obtenemos

$A = (\frac{-1-\sqrt{3}}{2},\frac{1+\sqrt{3}}{2})$

C = (1,2)

Usando la fórmula de la distancia, AC

$AC = \sqrt{(1-\frac{-1-\sqrt{3}}{2})^2+(2-\frac{1+\sqrt{3}}{2})^2}\\ AC = \sqrt{(\frac{2+1+\sqrt{3}}{2})^2+(\frac{4-1-\sqrt{3}}{2})^2}\\ AC = \sqrt{(\frac{3+\sqrt{3}}{2})^2+(\frac{3-\sqrt{3}}{2})^2}\\ AC = \sqrt{\frac{9+3+6\sqrt{3}+9+3-6\sqrt{3}}{4}}\\ AC = \sqrt{\frac{24}{4}}\\ AC = \sqrt{6}$

Área del triángulo equilátero ABC,

$= \frac{\sqrt{3}}{4}(side)^2\\ = \frac{\sqrt{3}}{4}(\sqrt{6})^2\\ = \frac{\sqrt{3}}{4}(6)\\ = \frac{3\sqrt{3}}{2}$ unidad cuadrada

Pregunta 10: Dos lados de un triángulo isósceles están dados por las ecuaciones 7x-y+3=0 y x+y-3=0 y su tercer lado pasa por el punto (1,-10). Determinar la ecuación del tercer lado.

Solución:

Sea la ecuación de la recta AB y AC 7x-y+3=0 y x+y-3=0 respectivamente.

∠B = ∠C

Pendiente de la recta AB: 7x-y+3=0

y = 7x+3

Pendiente m ₁ = 7

Pendiente de la línea AC: x+y-3=0

y = -x+3

Pendiente m ₂ = -1

Sea m la pendiente de la recta BC, que pasa por el punto (1,-10)

y-(-10) = m(x-1)

y+10 = m(x-1)

El ángulo entre las líneas AB y BC es igual al ángulo entre las líneas AC y BC, digamos θ

Como sabemos, dos líneas que tienen pendientes como m y M tendrán un ángulo θ entre ellas de la siguiente manera:

$\mathbf{tan θ = |\frac{M-m}{1+mM}|}$

Tomando signo positivo

tan θ = $\frac{m-7}{1+7m} = \frac{m-(-1)}{1+m(-1)}$

tan θ = $\frac{m-7}{1+7m} = \frac{m+1}{1-m}$

Resolviéndolo, obtenemos

m = -3 o $\frac{1}{3}$

Tomando signo negativo

tan θ = $\frac{m-7}{1+7m} = -\frac{m-(-1)}{1+m(-1)}$

tan θ = $\frac{m-7}{1+7m} = -\frac{m+1}{1-m}$

Resolviéndolo, obtenemos

m ² = -1 (lo cual no es posible)

Línea BC: cuando m = -3

y+10 = -3(x-1)

y+10 = -3x+3

3x+y-13=0

Línea BC: cuando m = $\frac{1}{3}$

$y+10 = \frac{1}{3}(x-1)$

3y+30 = x-1

x-3y-31=0

Pregunta 11: Muestre que el punto (3,-5) se encuentra entre las líneas paralelas 2x+3y-7=0 y 2x+3y+12=0 y encuentre la ecuación de las líneas a través de (3,-5) cortando las líneas anteriores en un ángulo de 45°.

Solución:

Sea la recta 1: 2x+3y-7=0

Línea 2: 2x+3y+12=0

Como la pendiente de la línea 1 y la línea 2 es la misma, estas líneas son paralelas.

Pendiente de las rectas M = $\frac{-2}{3}$

Para comprobar si (3,-5) se encuentra entre estas líneas

Tomando x=3 y y=-5

(2x+3y-7)(2x+3y+12)<0 (Si es cierto, entonces el punto se encuentra entre estas líneas)

(2(3)+3(-5)-7)(2(3)+3(-5)+12)

(6-15-7)(6-15+12)

(-16)(3) <0, que es un valor negativo.

Por lo tanto, el punto (3,-5) se encuentra entre las líneas.

Sea m la pendiente de la recta que pasa por el punto (3,-5)

y-(-5) = m(x-3)

y+5 = m(x-3)

Como se da, la línea corta por encima de las líneas en un ángulo de 45°.

Como sabemos, dos líneas que tienen pendientes como m y M tendrán un ángulo θ entre ellas de la siguiente manera:

$\mathbf{tan θ = |\frac{M-m}{1+mM}|}$

Tomando θ = 45° y M = $\frac{-2}{3}$

Tomando signo positivo

bronceado 45° = $|\frac{\frac{-2}{3}-m}{1+m(\frac{-2}{3})}|$

$1 = |\frac{\frac{-2-3m}{3}}{1-m(\frac{2}{3})}|$

$1 = |\frac{\frac{-2-3m}{3}}{\frac{3-2m}{3}}|$

$1 = |\frac{-2-3m}{3-2m}|$

Tendremos dos casos,

1 = $\frac{-2-3m}{3-2m}$ y 1 = $-\frac{-2-3m}{3-2m}$

3-2m = -2-3m y 3-2m = -(-2-3m)

3m-2m = -2-3 y 3-2m = 2+3m

m = -5 y 3m+2m = 3-2

m = -5 y m = $\frac{1}{5}$

Por lo tanto, la ecuación de la línea será,

cuando m = -5

y+5 = (-5)(x-3)

y+5 = -5x+15

5x+y-10=0

cuando m = $\frac{1}{5}$

y+5 = $\frac{1}{5}$ (x-3)

5y+25 = x-3

x-5y-28=0

Pregunta 12: La ecuación de la base de un triángulo equilátero es x+y=2 y su vértice es (2,-1). Encuentra la longitud y las ecuaciones de sus lados.

Solución:

∠A = ∠B = ∠C = 60°

Podemos decir que AC y AB forman 60° con BC.

Sea la pendiente de AC como m ₁ y AB como m ₂ que pasa por el punto (2,-1).

AB: (y-(-1)) = m ₁ (x-2)

y+1 = metro ₁ (x-2)

CA: (y-(-1)) = m ₂ (x-2)

y+1 = metro ₂ (x-2)

Pendiente de BC : x+y=2

y = -x+2

La pendiente de BC es -1.

Aquí, se da que estas dos líneas forman un ángulo de 60° entre ellas. Por eso,

Como sabemos, dos líneas que tienen pendientes como m y M tendrán un ángulo θ entre ellas de la siguiente manera:

$\mathbf{tan θ = |\frac{M-m}{1+mM}|}$

Aquí tenemos θ = 60°, m = m ₁ y m ₂ y M = -1

bronceado 60° = $|\frac{-1-m}{1+m(-1)}|$

√3= $|\frac{-1-m}{1-m}|$

Tendremos dos casos,

√3 = $\frac{-1-m}{1-m}$ y √3 = $-\frac{-1-m}{1-m}$

√3(1-m) = -1-m y √3(1-m) = 1+m

√3-√3m = -1-m y √3-√3m = m+1

√3m-m = √3+1 y +√3m+m = √3-1

m = $\frac{\sqrt{3}+1}{\sqrt{3}-1}$ y m = $\frac{\sqrt{3}-1}{\sqrt{3}+1}$

Después de racionalizar, obtenemos

m = $\frac{(\sqrt{3}+1)^2}{3-1}$ y m = $\frac{(\sqrt{3}-1)^2}{3-1}$

m = $\frac{1+3+2\sqrt{3}}{2}$ y m = $\frac{1+3-2\sqrt{3}}{2}$

m = 2+√3 y m = 2-√3

Por lo tanto, la ecuación de las rectas será,

AB: y+1 = metro ₁ (x-2)

y+1 = (2+√3)(x-2)

y+1 = (2+√3)x-4-2√3

(2+√3)xy-5-2√3=0 ……………….(yo)

CA: y+1 = m2 (x-2 ₎

y+1 = (2-√3)(x-2)

y+1 = (2-√3)x-4+2√3

(2-√3)xy-5+2√3=0 ……………….(ii)

Usando (ii) y x+y=2, obtenemos

$C = (\frac{15+\sqrt{3}}{6},-\frac{3+\sqrt{3}}{6})$

A = (2,-1)

Usando la fórmula de la distancia, AC

$AC = \sqrt{(2-\frac{15+\sqrt{3}}{6})^2+(-1-(-\frac{3+\sqrt{3}}{6}))^2}\\ AC = \sqrt{(\frac{12-15-\sqrt{3}}{6})^2+(\frac{-6+3+\sqrt{3}}{6})^2}\\ AC = \sqrt{(\frac{-3-\sqrt{3}}{6})^2+(\frac{-3+\sqrt{3}}{6})^2}\\ AC = \sqrt{\frac{9+3+6\sqrt{3}+9+3-6\sqrt{3}}{36}}\\ AC = \sqrt{\frac{24}{36}}\\ AC = \sqrt{\frac{2}{3}}$

CA = AB = BC = $\sqrt{\frac{2}{3}}$

Pregunta 13: Si dos vértices opuestos de un cuadrado son (1,2) y (5,8), encuentra las coordenadas de sus otros dos vértices y las ecuaciones de sus lados.

Solución:

Consideremos un cuadrado ABCD.

Según la propiedad del cuadrado, la diagonal biseca al ángulo.

Por lo tanto, ∠AOB = ∠AOD = 45°

Pendiente de la diagonal AC:

$\frac{8-2}{5-1} = \frac{6}{4} = \frac{3}{2}$

Sea m1 y m2 la pendiente de la recta AB y AD, que pasa por el punto (1,2)

AB: y-2 = m ₁ (x-1)

DA: y-2 = m ₂ (x-1)

Aquí se da que estas dos rectas forman un ángulo de 45° con AC. Por eso,

Como sabemos, dos líneas que tienen pendientes como m y M tendrán un ángulo θ entre ellas de la siguiente manera:

$\mathbf{tan θ = |\frac{M-m}{1+mM}|}$

Aquí, tenemos θ = 45°, m = m ₁ y m ₂ y M = $\frac{3}{2}$

bronceado 45° = $|\frac{\frac{3}{2}-m}{1+m(\frac{3}{2})}|$

$1 = |\frac{\frac{3-2m}{2}}{\frac{2+3m}{2}}|$

$1= |\frac{3-2m}{2+3m}|$

Tendremos dos casos,

1 = $\frac{3-2m}{2+3m}$ y 1 = $-\frac{3-2m}{2+3m}$

2+3m = 3-2m y 2+3m = -(3-2m)

3m+2m = 3-2 y 2+3m = 2m-3

5m = 1 y 3m-2m = -3-2

m = $\frac{1}{5}$ y m = -5

m = $\frac{1}{5}$ o -5

Por lo tanto, la ecuación de las rectas será,

AB: y-2 = m ₁ (x-1)

$y-2 = \frac{1}{5}(x-1)$

5y-10 = x-1

x-5y+9=0 ……………….(i)

DA: y-2 = m ₂ (x-1)

y-2 = -5(x-1)

y-2 = -5x+5

5x+y-7=0 ……………….(ii)

Como BC es paralelo a AD, entonces

La ecuación BC será 5x+y+λ=0 y como BC pasa por C(5,8), obtenemos

5(5)+(8)+λ=0

33+λ=0

λ = -33

Por lo tanto, la ecuación de BC es 5x+y-33=0 ……………….(iii)

Ahora como CD es paralelo a AB, entonces

La ecuación CD será x-5y+λ=0 y como CD pasa por C(5,8), obtenemos

5-5(8)+λ=0

-35+λ=0

λ = 35

Por lo tanto, la ecuación de CD es x-5y+35=0 ………………………(iv)

Resolviendo (i) y (iii), obtenemos

segundo(6,3)

Resolviendo (ii) y (iv), obtenemos

D(0,7)

Por lo tanto, la ecuación de las rectas es

AB = x-5y+9=0

BC = 5x+y-33=0

CD = x-5y+35=0

DA = 5x+y-7=0

Y los vértices del cuadrado son

A(1,2), B(6,3), C(5,8) y D(6,3)

Publicación traducida automáticamente

Artículo escrito por adi1212 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1: Encuentra la ecuación de las rectas que pasan por el origen y forman un ángulo de 45° con la recta √3x+y = 11.

Pregunta 2: Encuentra la ecuación de las rectas que pasan por el origen y son inclinadas en un ángulo de 75° a la recta x+y+√3(yx)=a.

Pregunta 3: Encuentra la ecuación de las rectas que pasan por (2,-1) y forman un ángulo de 45° con la recta 6x+5y-8=0.

Pregunta 4: Encuentra la ecuación de las rectas que pasan por el punto (h,k) y están inclinadas en un ángulo tan -1 m con respecto a la recta y=mx+c.

Pregunta 5: Encuentra la ecuación de las rectas que pasan por el punto (2,3) e inclinadas 45° a la recta 3x+y-5=0.

Pregunta 6: Hallar la ecuación de los lados de un triángulo rectángulo isósceles cuya ecuación de hipotenusa es 3x+4y=4 y el vértice opuesto es el punto (2,2).

Pregunta 7: La ecuación de un lado de un triángulo equilátero es xy=0 y un vértice es (2+√3,5). Demuestra que un segundo lado es y+(2-√3)x=6 y encuentra la ecuación del tercer lado.

Pregunta 8: Encuentra la ecuación de las dos rectas que pasan por (1,2) que forman dos lados de un cuadrado del cual 4x+7y=12 es una diagonal.

Pregunta 9: Encuentra la ecuación de las dos rectas que pasan por (1,2) y forman un ángulo de 60° con la recta x+y=0. Encuentra también el área del triángulo formado por las tres líneas.

Pregunta 10: Dos lados de un triángulo isósceles están dados por las ecuaciones 7x-y+3=0 y x+y-3=0 y su tercer lado pasa por el punto (1,-10). Determinar la ecuación del tercer lado.

Pregunta 11: Muestre que el punto (3,-5) se encuentra entre las líneas paralelas 2x+3y-7=0 y 2x+3y+12=0 y encuentre la ecuación de las líneas a través de (3,-5) cortando las líneas anteriores en un ángulo de 45°.

Pregunta 12: La ecuación de la base de un triángulo equilátero es x+y=2 y su vértice es (2,-1). Encuentra la longitud y las ecuaciones de sus lados.

Pregunta 13: Si dos vértices opuestos de un cuadrado son (1,2) y (5,8), encuentra las coordenadas de sus otros dos vértices y las ecuaciones de sus lados.

Deja una respuesta Cancelar la respuesta

Pregunta 4: Encuentra la ecuación de las rectas que pasan por el punto (h,k) y están inclinadas en un ángulo tan ^-1 m con respecto a la recta y=mx+c.