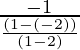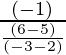Pregunta 1. Halla la ecuación de la recta que pasa por el punto (6, 2) y tiene pendiente -3.
Solución:
Sabemos (y – y 1 ) = m(x – x 1 )
Aquí, m = Pendiente de la línea = -3
x 1 = 6, y 1 = 2
Entonces, la ecuación de la recta es
⇒ y – 2 = (-3)(x – 6)
⇒ y – 2 = -3x + 18
⇒ 3x + y – 20 = 0
Pregunta 2. Halla la ecuación de la recta que pasa por (-2, 3) e inclinada formando un ángulo de 45° con el eje x.
Solución:
Sabemos y – y 1 = m(x – x 1 )
Aquí, m = Pendiente de la línea = tan 45° = 1
x1 = -2, y1 = 3
Entonces, la ecuación de la recta es
⇒ y – 3 = 1(x – (-2))
⇒ y – 3 = x + 2
⇒ x – y + 5 = 0
Pregunta 3. Encuentra la ecuación de la recta que divide el conjunto de los puntos (2, 3) y (-5, 8) en la razón 3:4 y también es perpendicular a ella.
Solución:
Sea P(x 1 , y 1 ) el punto en el que la línea divide la unión de los puntos (2, 3) y (-5, 8) en la razón 3:4
P(x1, y1) = \frac{(4 × 2 – 5 × 3)}{(3 + 4)}, \frac{(4 × 3 + 3 × 8)}{(3+4)}
= (-1, 36/7)
Pendiente de los puntos dados=(8-3)/(-5-2) =-5/7
Ya que, la línea requerida es perpendicular a la línea que une los puntos dados.
Por lo tanto, la pendiente de la línea requerida ‘m’ = 7/5
Aquí, x 1 = -1, y 1 = 36/7 y m = 7/5
Entonces, la ecuación de la recta es
⇒ y – 36/7 = 7/5(x – (-1))
⇒ y-36/7 = 7/5(x + 1)
⇒ 35y – 180 = 49x + 49
⇒ 49x + 35y + 229 = 0 es la ecuación requerida de la línea recta.
Cuestión 4. Demostrar que la perpendicular trazada desde el punto (4, 1) en la unión de (2, -1) y (6, 5) lo divide en razón 5:8.
Solución:
Sea PO la perpendicular trazada desde P(4,1) sobre la recta que une A(2, -1) y B(6, 5)
Sea la pendiente de PO ‘m’
segun pregunta
m × Pendiente de AB = -1
⇒ metro × (5 + 1)/(6 – 2) = -1
⇒ metro × 6/4 = -1
⇒ metro = -4/6 = -2/3
Así, la ecuación de la recta PO
x1 = 4, y1 = 1 y m = -2/3
(y-1) = -2/3(x-4)
⇒ 3y – 3 = -2x + 8
⇒ 2x + 3y – 11 = 0 ——–(1)
Sea O dividiendo la línea AB en la razón de K:1
Entonces las coordenadas de O son \frac{(6k + 2)}{(k + 1)}, \frac{(5k – 1)}{(k + 1)}
Como el punto O está en la línea AB
Por lo tanto, satisface la ecuación (1)
⇒ 12k + 4 + 15k – 3 – 11(k + 1) = 0
⇒ 27k – 11k + 1 – 11 = 0
⇒ 16k = 10
⇒ k = 5/8
Por lo tanto probado
Pregunta 5. Encuentra la ecuación de las alturas del triángulo cuyos puntos angulares son A(2, -2), B(1, 1) y C(-1, 0).
Solución:
Sean las altitudes AE, BF y CD
Pendiente de AE × Pendiente de BC = -1 [Dado que ambas rectas son perpendiculares entre sí]
Pendiente de AE = (-1) / Pendiente de BC
Pendiente de AE =
=
= -2
Ecuación de la altitud AE
y – (-2) = (-2)(x – 2)
⇒ y + 2 = -2x + 4
⇒ 2x + y – 2 = 0
Similarmente,
Pendiente de BF × Pendiente de AC = -1
Pendiente de BF =
=
= 3/2
Ecuación de la altitud BF
y – 1 = (3/2)(x – 1)
⇒ 2(y – 1) = 3x – 3
⇒ -3x + 2y – 2 + 3 = 0
⇒ 3x – 2y – 1 = 0
Pendiente de CD × Pendiente de AB = -1
Pendiente de CD=
=
= 1/3
Ecuación de la altitud CD
y – 0 = (1/3) (x – (-1))
⇒ 3y = x + 1
⇒ x – 3y + 1 = 0
Pregunta 6. Encuentra la ecuación de la bisectriz derecha del segmento de línea que une los puntos (3, 4) y (-1, 2).
Solución:
Sean los puntos del segmento de recta A(3, 4) y B(-1, 2)
Deje que la bisectriz derecha se encuentre en el punto ‘P’ en el segmento de línea
Coordenadas del punto P = \frac{(3-1)}{2}, \frac{(4+2)}{2} [Usando la fórmula del punto medio]
= (1, 3)
Pendiente de AB = [(2 – 4) / (-1 – 3)]
=-2/-4
= 1/2
Pendiente de la bisectriz derecha =
= -2
Ecuación de la bisectriz derecha
⇒ y – 3 = -2(x – 1)
⇒ y – 3 = -2x + 2
⇒ 2x + y – 5 = 0 es la ecuación requerida de la bisectriz derecha
Pregunta 7. Encuentra la ecuación de la línea recta que pasa por el punto (3, -2) y forma un ángulo de 60° con la dirección positiva del eje y.
Solución:
Como la recta forma un ángulo de 60° con la dirección positiva del eje y i
t forma un ángulo de 30° con la dirección positiva del eje x como se muestra en el diagrama.
Pendiente de la recta ‘m’= tan 30° = 1/√3
Ecuación de la recta que pasa por (3, -2)
y – (-2) = 1/√3(x – 3)
⇒ √3(y + 2) = x – 3
⇒ √3y + 2√3 = x – 3
⇒ x – √3y – 3 – 2√3 = 0 es la ecuación requerida de la línea recta.
Pregunta 8. Encuentra la ecuación de la recta que pasa por el punto (1, 2) y forma un ángulo con la dirección positiva del eje x cuyo seno es 3/5.
Solución:
Dado, sen θ = 3/5
tan θ = 3/√(25 – 9) = 3/4
Pendiente de la línea m = 3/4
Ecuación de la recta que pasa por (1, 2)
y-2 = 3/4(x-1)
⇒ 4(y – 2) = 3x – 3
⇒ 4y – 8 = 3x – 3
⇒ 3x – 4y + 5 = 0 es la ecuación requerida de la línea recta.
Pregunta 9. Halla la ecuación de la recta que pasa por el punto (-3, 5) y es perpendicular a la recta que une (2, 5) y (-3, 6).
Solución:
Pendiente de la ecuación requerida ‘m’ = (-1) / [Pendiente de la línea que une (2, 5) y (-3, 6)] [Perpendiculares entre sí]
metro =
metro =
metro = 5
Ecuación de la recta que pasa por (-3, 5)
y-5 = 5(x-(-3))
⇒ y – 5 = 5x + 15
⇒ 5x – y + 20 = 0 es la ecuación requerida de la línea recta.
Pregunta 10. Halla la ecuación de la bisectriz derecha del segmento de recta que une los puntos A(1, 0) y B(2, 3).
Solución:
Deje que la bisectriz derecha se encuentre en el punto ‘P’ en el segmento de línea
Coordenadas del punto P = [
] [Usando la fórmula del punto medio]
= (3/2, 3/2)
Pendiente de AB = [(3 – 0)/(2 – 1)]
= 3/1 = 3
Pendiente de la bisectriz derecha = -1/3
Ecuación de la bisectriz derecha
⇒ y – 3/2 = -1/3(x – 3/2)
⇒ 3(y – 3/2) = -x + 3/2
⇒ x + 3y – 9/2 – 3/2 = 0
⇒ x + 3y – 6 = 0
⇒ x + 3y – 6 = 0 es la ecuación requerida de la bisectriz derecha.
Pregunta 11. Encuentra las rectas que pasan por el punto (0, 2) formando ángulos π/3 y 2π/3 con el eje x. Además, encuentre las líneas paralelas a ellas que cortan el eje y a una distancia de 2 unidades por debajo del origen.
Solución:
Dada la recta que pasa por el punto (0, 2) formando ángulos π/3 y 2π/3 con el eje x
.Pendiente m1= tan π/3 = √3
Pendiente m2 = tan 2π/3 = -√3
Ecuación de las líneas requeridas
⇒ y – 2 = √3(x – 0) y y – 2 = -√3(x – 0)
⇒ y – √3x – 2 = 0 y y + √3x – 2 = 0
Ahora, la ecuación de la línea paralela a la línea que tiene pendiente m1 y intersección en y c= -2
y = m1x + c
⇒ y = √3x – 2
De manera similar, la ecuación de la línea paralela a la línea que tiene pendiente m2 y intersección en y c = -2
y= m2x + c
⇒ y = -√3x – 2
Pregunta 12. Encuentra la ecuación de las líneas rectas que cortan una intersección 5 desde el eje y y están igualmente inclinadas a los ejes.
Solución:
Dado que las líneas rectas cortan una intersección 5 del eje y y están igualmente inclinadas a los ejes.
La pendiente de las dos líneas es m1= tan 45° =1 y m2 = tan 135° = -1
La ecuación de las rectas requeridas es
y = m1x + c o y = m2 + c
⇒ y = x +5 o y = -x + 5
⇒ y = x +5 o y + x = 5
Pregunta 13. Encuentra la ecuación de líneas rectas que intercepta una longitud 2 en la dirección positiva del eje x y está inclinada en un ángulo de 135° con la dirección positiva del eje y.
Solución:
La línea requerida que está inclinada en un ángulo de 135° con la dirección positiva del eje y forma un ángulo de 45° con el eje x positivo.
Pendiente de la línea requerida m = tan 45° = -1
Ecuación de la línea recta requerida con intersección x c = 2 y m = -1
x = mi + c
⇒x = 1y + 2
⇒ x – y – 2 = 0
Pregunta 14. Encuentra la ecuación de la recta que pasa por (0, 0) con pendiente m.
Solución:
La ecuación de la recta que pasa por (0, 0) con pendiente m es
y-0 = m(x-0)
⇒ y = mx
Pregunta 15. Encuentra la ecuación de la línea que pasa por (2, 2√3) e inclinada con el eje x en un ángulo de 75°.
Solución:
Pendiente de la línea m = tan 75°
= bronceado (45° + 30°)
= (tan 45° + tan 30°) /(1 – tan 45° tan 30°)
= (1 + 1/√3)/(1 – 1/√3)
metro = (√3 + 1)/(√3 – 1) = 2 + √3
Ecuación de la línea requerida que pasa por (2, 2√3) con pendiente de 2 + √3
y – 2√3 = (2 + √3)(x – 2)
⇒ y – 2√3 = (2 + √3)x – 4 – 2√3
⇒ (2 + √3)x – y – 4 = 0
Pregunta 16. Encuentra la ecuación de la línea que pasa por (1, 2) y forma un ángulo de 30° con el eje y.
Solución:
Consideremos una ecuación de línea que pasa por puntos (x 1 , y 1 ) que forman un ángulo θ con el eje x.
(y – y 1 ) = tanθ(x – x 1 ) -(1)
Dado: Punto = (1, 2), y ángulo = 30°(con eje y)
Entonces, ángulo con el eje x = 90° – 30° = 60°
Ahora ponga todos estos valores en la ecuación (1), obtenemos
(y – 2) = tan60°(x – 1)
(y-2) = √3(x-1)
y – 2 = √3x – √3
√3x – √3 – y + 2 = 0
√3x – y – √3 + 2 = 0
Publicación traducida automáticamente
Artículo escrito por rahulsharma1771996 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

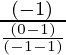
![Rendered by QuickLaTeX.com \frac{(-1)}{[\frac{(0 - (-2))}{(-1 - 2)}]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a404a2e99dc7185936f5b8b3e95aea4a_l3.png)