Clase 11 RD Sharma Solutions – Capítulo 23 Las Líneas Rectas – Ejercicio 23.5

Pregunta 1. Encuentra la ecuación de la línea recta que pasa por el siguiente par de puntos. 

(i) (0, 0) y (2, -2) 

Solución:

Aquí, los dos puntos son (x ₁ , y ₁ ) = (0, 0) y (x ₂ , y ₂ ) = (2, -2).

Entonces la ecuación de la recta en forma de dos puntos es

y – y ₁ = (y ₂ – y ₁ ) / (x ₂ – x ₁ )(x – x ₁ )  

y – 0 = [(-2 – 0)/(2 – 0)] (x – 0)

⇒ y = (-1)x

⇒ y = -x

(ii) (a, b) y (a + c sen α, b + c cos α)

Solución:

Aquí, los dos puntos son (x ₁ , y ₁ ) = (a, b) y (x ₂ , y ₂ ) = (a + c sin α, b + c cos α).

Entonces la ecuación de la recta en forma de dos puntos es

y – b = (b + c cos α – b)/(a + c sen α – a)(x- a)

⇒ y – b = (cos α/sen α)(x – a)

⇒ y – b = cuna α(x – a)

(iii) (0, -a) y (b, 0)

Solución:

Aquí, los dos puntos son (x ₁ , y ₁ ) = (0, -a) y (x ₂ , y ₂ ) = (b, 0).

Entonces la ecuación de la recta en forma de dos puntos es

y – (-a) = (0 – (-a))/(b – 0)(x – 0)

⇒ b(y + a) = eje

⇒ hacha – por = ab

(iv) (a, b) y (a + b, a – b)  

Solución:

Aquí, los dos puntos son (x ₁ , y ₁ ) = (a, b) y (x ₂ , y ₂ ) = (a + b, a – b).

Entonces la ecuación de la recta en forma de dos puntos es

y – b = (a – b – b)/(a + b – a)(x – a)

⇒ y – b = (a – 2b)/b (x – a)

⇒ y – b = (a – 2b)x + a ² – 2ab

⇒ (a – 2b)x – por + b ² + 2ab – a ² = 0

(v) (a ₁ ,a/t ₁ ) y (a ₂ , a/t ₂ )

Solución:

Aquí, los dos puntos son (x ₁ , y ₁ ) = (en ₁ , a/t ₁ ) y (x ₂ , y ₂ ) = (en ₂ , a/t ₂ ).

Entonces la ecuación de la recta en forma de dos puntos es

y – a/t ₁ = (a/t ₂ – a/t ₁ ) / (en ₂ – en ₁ )(x – en ₁ )  

⇒ y – a/t ₁ = ((en ₁ – en ₂ )/t ₁ t ₂ )/(en ₂ – en ₁ )(x – en ₁ )

⇒ t ₁ t ₂ y – en ₂ = (-1)(x – en ₁ )

⇒ t ₁ t ₂ y + x = en ₁ + en ₂

(vi) (a cos α, a sen α) y (a cos β, a sen β) 

Solución:

Aquí, los dos puntos son (x1, y1) = (a cos α, a sen α) y (x2, y2) = (a cos β, a sen β).

Entonces la ecuación de la recta en forma de dos puntos es

y – a sin α =(a sin β – a sin α)/(a cos β – a cos α)(x – a cos α)  

⇒ y – a sen α = [2 cos (β + α)/2 sen (β – α)/2] / [-2 sen (β + α)/2 sen (β – α)/2](x – a cos a)

⇒ y – a sin α = -[cos (β + α)/2]/[sin (β + α)/2](x – a cos α)

⇒ x cos (β + α)/2 + y sen (β + α)/2 = a(sen α [sen (β + α)/2] + cos α [cos (β + α)/2])

⇒ x cos (β + α)/2 + y sen (β + α)/2 = a cos (α – β/2 – α/2)

⇒ x cos (β + α)/2 + y sen (β + α)/2 = a cos (α/2 – β/2)

Pregunta 2. Encuentra las ecuaciones de los lados del triángulo cuyas coordenadas son respectivamente los puntos angulares.

(i) (1, 4), (2, -3) y (-1, -2)

Solución:

Dado: Puntos A (1, 4), B (2, -3) y C (-1, -2). 

Ecuación de la recta que pasa por los dos puntos (x ₁ , y ₁ ) y (x ₂ , y ₂ )  

y – y ₁ = [(y ₂ – y ₁ )/(x ₂ – x ₁ )] (x – x ₁ ) 

Ecuación de los lados AB, 

Usando la fórmula anterior 

y – 4 = [(-3 – 4)/(2 – 1)](x – 1)

⇒ y – 4 = -7x + 7

⇒ y + 7x = 11

Similarmente

 Ecuación de los lados BC

 ⇒ y + 3 = [(-2 – (-3))/(-1 – 2)](x – 2) 

y + 3 = (-1/3) (x – 2) 

⇒ 3y + 9 = -x + 2 

⇒ 3y + x = – 7

⇒ x + 3y + 7 = 0 

Y ecuación de los lados CA 

⇒ y + 2 = [(4 – (-2))/(1 – (-1))](x + 1) 

⇒ y + 2 = 3(x + 1)

⇒ y + 2 = 3x + 3

⇒ y – 3x = 1 

La ecuación de los lados requeridos del triángulo son y + 7x = 11, x+ 3y + 7 =0 y y – 3x = 1

(ii) (0, 1), (2, 0) y (-1, -2)  

Solución:

Dados los Puntos A (0, 1), B (2, 0) y C (-1, -2). 

La ecuación de la recta que pasa por los dos puntos (x ₁ , y ₁ ) y (x ₂ , y ₂ ) 

 y – y ₁ = [(y ₂ – y ₁ )/(x ₂ – x ₁ )] (x – x ₁ ) 

Ecuación de los lados AB,

Usando la fórmula anterior 

 y – 1 = [(0 – 1)/(2 – 0)](x – 0) 

⇒ y – 1 = -1/2 x 

⇒ 2y – 2 = -x 

⇒ x + 2y = 2 

Ecuación de los lados BC

y – 0 = [(-2 – 0)/(-1 – 2)](x – 2) 

⇒ y – 0 = (-2/3)(x – 2) 

⇒ 3y = -2x + 4

⇒ 2x – 3y = 4 

Ecuación de los lados CA

⇒ y – (-2) = [(1 + 2)/(1 + 0)](x – (-1))

⇒ y + 2 = 3(x + 1) 

⇒ y + 2 = 3x + 3 

⇒ y – 3x = 1

La ecuación requerida de los lados del triángulo es x + 2y = 2, 2x – 3y = 4, y y – 3x = 1

Pregunta 3. Encuentra las ecuaciones de las medianas de un triángulo cuyas coordenadas son (-1, 6), (-3, -9) y (5, -8) vértices.

Solución:

Sean A (−1, 6), B (−3, −9) y C (5, −8) las coordenadas del triángulo dado y 

D, E y F sean los puntos medios de AB, BC y AC, respectivamente. 

Coordenada del punto medio de AB = D[(-1 – 3)/2, (6 – 9)/2]

= D(-2, -3/2) 

CD mediana pasa por C (5, -8) y D (-2, -3/2)

Entonces, usando la fórmula (y – y ₁ ) = [(y ₂ – y ₁ )/(x ₂ – x ₁ )] (x – x ₁ ) 

(y – (-8)) = [(-3/2 – (-8))/(-2 – 5)] (x – 5)

⇒ y + 8 = -13/14(x-5)

⇒ 14y + 112 = -13x + 65

⇒ 13x + 14y + 47 = 0

Coordenada del punto medio de BC = E[(-3 + 5)/2, (-9 – 8)/2]

= E(1, -17/2) 

La mediana AE pasa por A (-1, 6) y E (1, -17/2) 

Usando la fórmula de dos puntos

⇒ y – 6 = -29/4 (x + 1)

⇒ 4y – 24 = -29x – 29 

⇒ 29x + 4y + 5 = 0

Coordenada del punto medio de AC = F[(-1 + 5)/2, (6 – 8)/2]

= E(2, -1) 

Del mismo modo, Median BF pasa por B (-3,-9) y F (2,-1) 

Usando la fórmula, 

y – (-9) = [(-1 – (-9))/(2 – (-3))] (x – (-3)) 

⇒ y + 9 = 8/5 (x + 3)

⇒ 5y + 45 = 8x + 24

⇒ 8x – 5y – 21 = 0

La ecuación de las medianas requeridas del triángulo son: 29x + 4y + 5 = 0, 8x – 5y – 21 = 0, y 13x + 14y + 47 = 0

Pregunta 4. Encuentra las ecuaciones de las diagonales del rectángulo cuyas ecuaciones de lados son x = a, x = a’, y = b y y = b’.

Solución:

Dado,

La ecuación de los lados del rectángulo es x = a, x = a’, y = b y y = b’ 

Así, los vértices del rectángulo son A (a, b), B (a’, b), C (a’, b’) y D (a, b’)

 Ecuación de la diagonal que pasa por A (a, b) y C (a’, b’) 

 Usando la fórmula (y – y ₁ ) = [(y ₂ – y ₁ )/(x ₂ – x ₁ )] (x – x ₁ ) 

⇒ y – b = [(b’ – b)/(a’ – a)] (x – a)

⇒ (a’ – a)y – b(a’ – a) = (b’ – b)x – a(b’ – b) 

⇒ (a’ – a) – (b’ – b)x = ba’ – ab’ 

De manera similar, la ecuación de la diagonal que pasa por B (a’, b) y D (a, b’)

 Usando la fórmula de dos puntos, 

⇒ y – b = [(b’ – b)/(a – a’)] (x – a’)

⇒ (a – a’)y – b(a – a’) = (b’ – b)x – a’ (b’ – b) 

⇒ (a’ – a)y + (b’ – b)x = a’b’ – ab 

La ecuación requerida de las diagonales es y(a’ – a) – x(b’ – b) = a’b – ab’ y y(a’ – a) + x(b’ – b) = a’b’ – abdominales

Pregunta 5. Halla la ecuación del lado BC del triángulo ABC cuyos vértices son A(-1, -2), B(0, 1) y C(2, 0) respectivamente. Además, encuentre la ecuación de la mediana a través de (-1, -2).

Solución:

La ecuación del lado BC del triángulo ABC es

(y – 1) = [(0 – 1)/(2 – 0)] (x – 0)

⇒ (y – 1) = (-1/2)x

⇒ x + 2y – 2 = 0

Punto medio de (0, 1) y (2, 0)

= [(0 + 2)/2, (1 + 0)/2]

= (1, 1/2)

Ecuación de la mediana a través de (-1, -2) y (1, 1/2)

(y – (-2)) = [(1/2 + 2)/(1 + 1)](x – (-1))

⇒ y + 2 = 5/4(x + 1)

⇒ 4y + 8 = 5x + 5

⇒ 5x – 4y – 3 = 0 es la ecuación requerida de la mediana.

Pregunta 6. Utilizando el concepto de ecuación de línea, demuestre que los tres puntos (3, 0), (-2, -2) y (8, 2) son colineales.

Solución:

Para mostrar que los puntos (-2, -2), (8, 2) y (3, 0) son colineales,

La ecuación de la recta que pasa por los puntos (3, 0), (-2, -2) es

(y − 0) = [(−2 − 0)/(−2 − 3)](x − 3)

y = -2/−5(x − 3)

5y = 2x − 6

2x − 5y = 6

Ahora, poniendo el tercer punto en la ecuación anterior para comprobar si se cumple o no.

IZQ = 2 × 8 − 5 × 2

= 16 − 10

= 6 = lado derecho

Por tanto, la recta que pasa por los puntos (3, 0) y (-2, -2) también pasa por el punto (8, 2).

Por lo tanto, los puntos (3,0), (-2, -2) y (8, 2) son colineales.

Pregunta 7. Demostrar que la línea y- x+ 2 = 0 divide la unión de los puntos (3, -1) y (8, 9) en la razón 2:3.

Solución: 

Supongamos que la línea y- x+ 2=0 divide la unión de los puntos (3, -1) y (8, 9) en la razón 2:3. 

La coordenada del punto de división debe estar en la línea dada.

 Coordenada del punto de división = [(8×2+ 3×3) / (2+3), (9×2-3) / (2+ 3)]

= (25/5, 15/ 5) = (5, 3)

Poniendo esta coordenada en y – x + 2 = 0 

= 3 – 5 + 2

= -2 + 2 = 0

Así, vemos que la coordenada satisface la r = ecuación de la recta que 

demuestra que la línea divide la unión de puntos en la razón de 2:3.

Pregunta 8. Encuentra la ecuación de la línea recta que biseca la distancia entre los puntos (a, b) y (a′, b′) y también biseca la distancia entre los puntos (−a, b) y (a′, − b’).

Solución:

Los puntos que bisecan los puntos dados son (x1, y1) = (a + a′/2, b + b′/2) y (x2, y2) = (-a + a′/2, b − b′/ 2) 

Usando la fórmula de dos puntos  

(y − y ₁ ) = [(y ₂ − y ₁ )/(x ₂ − x ₁ )](x − x ₁ ) 

[y – (b + b’)/2] = 

⇒ (2y – b – b’)/2 = b’/a (2x – a – a’)/2

⇒ 2ay – ab – ab’ = 2b’x – ab’ – a’b’

⇒ 2ay – 2b’x + a’b’ – ab = 0 Es la ecuación requerida de la recta

Pregunta 9. ¿En qué proporción se divide la recta que une los puntos (2, 3) y (4, -5) entre la recta que pasa por los puntos (6, 8) y (-3, -2)?

Solución:

Ecuación de la recta que une (6, 8) y (-3, -2)

y – 8 = [(-2 – 8)/(-3- 6)](x – 6)

⇒ Y – 8 = 10/9(x – 6)

⇒ 9Y – 72 = 10x – 60

⇒ 10x – 9y + 12 = 0

Sea la razón en que los puntos (2, 3) y (4, -5) divididos por k : 1

P[(4k + 2)/(k + 1), (-5k + 3)/(k + 1)]

Ponemos este punto en la recta anterior ya que satisface la ecuación anterior

 10 (4k + 2)/(k + 1) – 9(-5k + 3)/ (k + 1) + 12 = 0

40k + 20 + 45k – 27 + 12k + 12 = 0

97k + 5 = 0

k = -5/97

o k = 5/97 (Externo)

Pregunta 10. Los vértices de un cuadrilátero son A(-2, 6), B(1, 2) C(10, 4) y D(7, 8). Encuentra la ecuación de su diagonal.

Solución:

Dado A(−2, 6), B(1, 2), C(10, 4) y D(7, 8)

Las diagonales son AC y BD.

Ecuación de la línea AC

y − 6 = [(4 – 6)/(10 – (-2))] (x − (-2))

⇒ y − 6 = (-2/12)(x + 2)

⇒ 6y – 36 = -x – 2

⇒ x + 6y − 34 = 0

Ecuación de la línea BD

y − 2 = [(8 – 2)/(7 – 1)] (x − 1)

⇒ y – 2 =(6/6)(x-1)

⇒ y – 2 = x – 1

⇒ x – y + 1 = 0

Entonces, la ecuación requerida es x + 6y − 34 = 0 y x − y + 1 = 0

Pregunta 11. La longitud L (en centímetros) de una varilla de cobre es una función lineal de su temperatura Celsius C. En un experimento, si L = 124.942 cuando C = 20 y L = 125.134 cuando C = 110, exprese L en términos de C.

Solución:

Supongamos que C está a lo largo del eje x y L a lo largo del eje y

 Tenemos dos puntos (20, 124.942) y (110, 125.134) 

La relación lineal entre L y C viene dada por la ecuación de 

la recta que pasa por los puntos (20, 124.942) y (110, 125.134)

(L− 124,942) = (125,134 − 124,942) / (110 − 20)(C − 20)

⇒ L −124,942 = 0,192/90(C − 20)

⇒ L = 0.192/ 90(C − 20) + 124.942 es la relación lineal requerida.

Pregunta 12. El dueño de una tienda de leche descubre que puede vender 980 litros de leche cada semana a Rs 14 por litro y 1220 litros de leche a Rs 16 por litro. Suponiendo una relación lineal entre el precio de venta y la demanda, ¿cuántos litros podría vender semanalmente a Rs 17 por litro?

Solución:

Dado, 

980 litros de leche se venden a Rs 14 por litro

1220 litros de leche se venden a Rs 16 por litro

Supongamos la cantidad de leche en el eje y y el precio de venta en el eje x.

Podemos decir que la recta pasa por A(14, 980), B(16, 1220) y C(17, x)

Dado que existe una relación lineal entre el precio de venta y la demanda

Por lo tanto, Pendiente de AB= Pendiente BC

(1220 – 980)/(16 – 14) = (x – 1220)/(17 – 16)

⇒ 240/2 = x – 1220 / 1

x = 1340 litros de leche que podría vender semanalmente a Rs 17 por litro 

Pregunta 13. Encuentra la ecuación de la bisectriz del ángulo A del triángulo cuyos vértices son A(4, 3), B(0, 0) y C(2, 3).

Solución:

Sea AD la bisectriz del ángulo A

Entonces BD : DC = AB : AC

|AB| = √((4 – 0) ² + (3 – 0) ² ) = 5

|CA| = √((4 – 2) ² + (3 – 3) ² ) = 2

⇒ BD/DC = AB/AC = 5/2

es decir, D divide a BC en la proporción de 5:2

Ahora, las coordenadas de D son \frac{(5×2 +0)}{5+2}, \frac{(5×3+0)}{5+2} = (10/7, 15/7)

La ecuación requerida de la bisectriz AD=

Usando la fórmula de dos puntos

y-3 = [ )](x-4)

⇒ y – 3 = [(15 – 21)/(10 – 28)](x – 4)

⇒ y – 3 = 1/3 (x – 4)

⇒ 3y – 9 = x – 4

⇒ x – 3y + 5 = 0

Pregunta 14. Encuentra las ecuaciones de la recta que pasa por el origen y triseca la porción de recta 3x + y = 12 que es interceptada entre los ejes de coordenadas.

Solución:

Para encontrar el punto de intercepción ponemos x = 0 y y = 0.

3x + y = 12

x = 0 ⇒ y = 12

y = 0 ⇒ x = 4

Entonces la recta se intercepta entre A(4, 0) y B(0, 12)

Sean los puntos P y Q trisecan la porción de la recta AB

Ahora P divide a AB en 1:2

= P \frac{(1(0) + 2(4))}{(1 + 2)}, \frac{(1(12) + 2(0))}{(1 + 2)}

= P(8/3, 4)

Entonces la ecuación de la línea que une el origen y P es  

y − 0 = [(4 – 0)/(8/3 – 0)](x – 0)

y = (12/8)x = (3/2)x

Ahora Q divide AP en 1:1, 

= Q[(8/3 + 0)/2, (4 + 12)/2]

= Q(4/3, 8)

La ecuación de la recta que une el origen con Q es  

y – 0 = [(8 – 0)/(4/3 – 0)](x – 0) 

y = (24/4)x = 6x

Entonces, las ecuaciones requeridas son y = 6x y 2y = 3x.

Pregunta 15. Halla la ecuación de las diagonales del cuadrado formado por las rectas x = 0, y = 0, x = 1 e y = 1.

Solución:

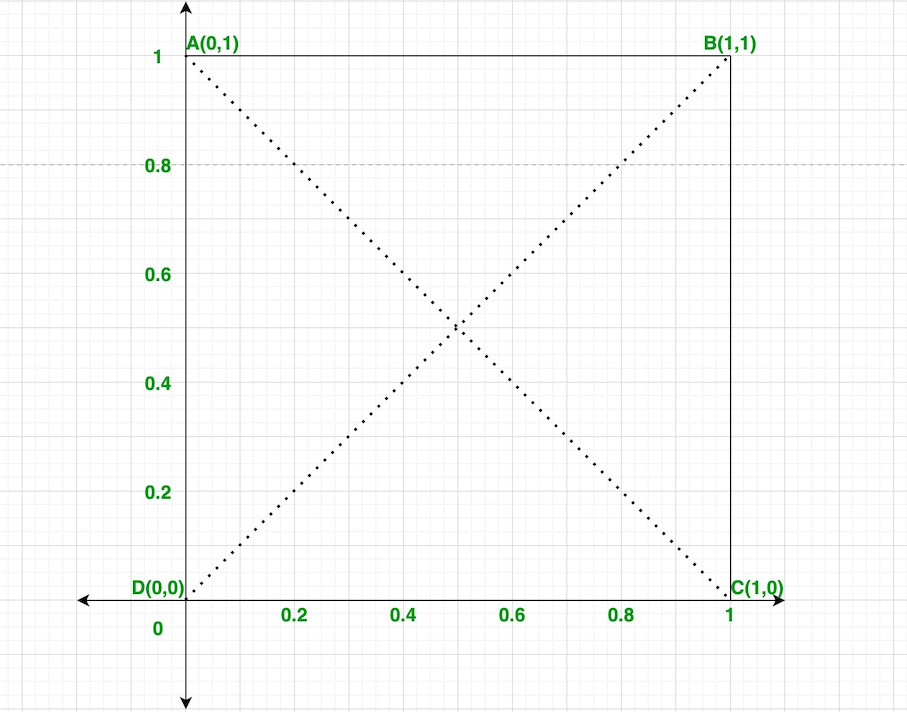
De la gráfica, obtenemos cuatro puntos, es decir, A(0, 1), B(1, 1), C(1, 0) y D(0, 0).

Ahora consideremos que D1 es la diagonal formada al unir los puntos B y D, 

y D2 es la diagonal formada por los puntos A y C.

Entonces, encontramos la ecuación de la diagonal D1:

(y – 1) = 

(y – 1) = (1)(x – 1)

y = x

 Entonces, encontramos la ecuación de la diagonal D2:

(y – 1) = 

(y – 1) = (-1)(x)

y + x = 1