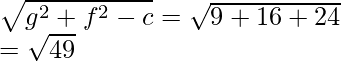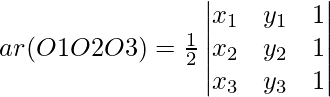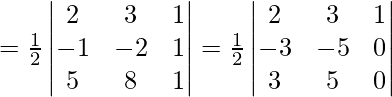Clase 11 Soluciones RD Sharma – Capítulo 24 El Círculo – Ejercicio 24.2

Posted on by Rudeus Greyrat

Pregunta 1(i). Encuentra las coordenadas del centro y el radio del círculo x 2 + y 2 + 6x – 8y – 24 = 0.

Solución:

Como sabemos que la ecuación general de las circunferencias es

x 2 + y 2 + 2gx + 2fy + c = 0 …..(i)

Centro = (-g, -f)

Radio = \sqrt{g^2+f^2-c}

La ecuación dada del círculo es x 2 + y 2 + 6x – 8y – 24 = 0

Al comparar con la ecuación (i), obtenemos

Por lo tanto, g = 3, f = -4, c = -24

Asi que, 

Centro = (-3, 4)

Radio = \sqrt{g^2+f^2-c}=\sqrt{9+16+24}\\ =\sqrt{49}

Radio = 7

Pregunta 1(ii). Encuentra las coordenadas del centro y el radio del círculo 2x 2 + 2y 2 – 3x + 5y = 7.

Solución:

Como sabemos que la ecuación general de las circunferencias es

x 2 + y 2 + 2gx + 2fy + c = 0 …..(i)

Centro = (-g, -f)

Radio = \sqrt{g^2+f^2-c}

La ecuación dada del círculo es 2x 2 + 2y 2 – 3x + 5y – 7 = 0

x2 + y2 – 3 /2x + 5/2y – 7/2 = 0

Al comparar con la ecuación (i), obtenemos

Por lo tanto, g = -3/4, f = 5/4, c = -7/2

Entonces, centro = (3/4, -5/4)

Radio = \sqrt{(\frac{3}{4})^2+(-\frac{5}{4})^2+\frac{7}{2}}\\ =\sqrt{\frac{9}{16}+\frac{25}{16}+\frac{7}{2}}=\sqrt{\frac{90}{4}}

Radio = 3√10/4 

Pregunta 1(iii). Encuentra las coordenadas del centro y el radio del círculo 1/2(x 2 + y 2 ) + x cosθ + y sinθ – 4 = 0.

Solución:

Como sabemos que la ecuación general de las circunferencias es

x 2 + y 2 + 2gx + 2fy + c = 0 …..(i)

Centro = (-g, -f)

Radio = \sqrt{g^2+f^2-c}

La ecuación dada del círculo es 1/2(x 2 + y 2 ) + x cosθ + y sinθ – 4 = 0

⇒ x 2 + y 2 + 2x cosθ + 2sen θ – 8 = 0

Al comparar con la ecuación (i), obtenemos

Por lo tanto, g = cos θ, f = sen θ, c = -8

Entonces, centro = (-cos θ, -sinθ)

Radio = \sqrt{\cos^2θ+\sin^2θ+8}=\sqrt{1+8}=3

Radio = 3

Pregunta 1(iv). Encuentra las coordenadas del centro y el radio del círculo x 2 + y 2 – ax – by = 0.

Solución:

Como sabemos que la ecuación general de las circunferencias es

x 2 + y 2 + 2gx + 2fy + c = 0 …..(i)

Centro = (-g, -f)

Radio = \sqrt{g^2+f^2-c}

Dada la ecuación del círculo es x 2 + y 2 – ax – by = 0

Al comparar con la ecuación (i), obtenemos

Por lo tanto, g = -a/2, f = -b/2, c = 0  

Entonces, centro = (a/2, b/2) 

Radio = \sqrt{\frac{a^2}{4}+\frac{b^2}{4}+0}=\frac{\sqrt{a^2+b^2}}{2}

Radio = \frac{a^2+b^2}{2}

Pregunta 2(i). Encuentra la ecuación del círculo que pasa por los puntos (5, 7), (8, 1) y (1, 3).

Solución:

Dado que, el círculo pasa por los puntos P(5, 7), Q(8, 1) y R(1, 3)

Como sabemos que la ecuación general de las circunferencias es

x 2 + y 2 + 2gx + 2fy + c = 0 …..(i)

Dado que P, Q y R se encuentran en la ecuación (i)

Asi que, 

25 + 49 + 10g + 14f + c = 0 …….(ii)

64 + 1 + 16g + 2f + c = 0 …….(iii)

1 + 9 + 2g + 6f + c = 0 ……(iv)

Ahora, al resolver las ecuaciones (ii), (iii) y (iv), obtenemos,

g = -29/6, f = -19/6, c = 56/3

Ahora ponga todos estos valores en la ecuación (i), obtenemos

la ecuacion del circulo es  

x2 + y2 – 29 /3x – 19/6y + 56/3 = 0 

3(x2 + y2 ) – 29x – 19y + 56 = 0

Pregunta 2(ii). Encuentra la ecuación del círculo que pasa por los puntos (1, 2), (3, -4) y (5, -6).

Solución:

Dado que, el círculo pasa por los puntos P(1, 2), Q(3, -4) y R(5, -6)

Como sabemos que la ecuación general de las circunferencias es

x 2 + y 2 + 2gx + 2fy + c = 0 …..(i)

Dado que P, Q y R se encuentran en la ecuación (i)

Asi que, 

1 + 4 + 2g + 4f + c = 0 …..(ii)

9 + 16 + 6g – 8f + c = 0 …..(iii)

25 + 36 + 10g – 12f + c = 0 …..(iv)

Ahora, al resolver las ecuaciones (ii), (iii) y (iv), obtenemos,

g = -11, f = -2 y c = 25

Ahora ponga todos estos valores en la ecuación (i), obtenemos

la ecuacion del circulo es  

x2 + y2 – 22x – 4y + 25 = 0

Pregunta 2(iii). Encuentra la ecuación del círculo que pasa por los puntos (5, -8), (-2, 9) y (2, 1).

Solución:

Dado que, el círculo pasa por los puntos P(5, -8), Q(-2, 9) y R(2, 1)

Como sabemos que la ecuación general de las circunferencias es

x 2 + y 2 + 2gx + 2fy + c = 0 …..(i)

Dado que P, Q y R se encuentran en la ecuación (i)

Asi que, 

25 + 64 + 10g – 16f + c = 0 …..(ii)

4 + 81 – 4g + 18f + c = 0 …..(iii)

4 + 1 + 4g + 2f + c = 0 …..(iv)

Ahora, al resolver las ecuaciones (ii), (iii) y (iv), obtenemos,

g = 58, f = 24 y c = -285

Ahora ponga todos estos valores en la ecuación (i), obtenemos

la ecuacion del circulo es  

x2 + y2 + 116x + 48y – 285 = 0         

Pregunta 2(iv). Encuentra la ecuación del círculo que pasa por los puntos (0, 0), (-2, 1) y (-3, 2).

Dado que, el círculo pasa por los puntos P(0, 0), Q(-2, 1) y R(-3, 2)

Como sabemos que la ecuación general de las circunferencias es

x 2 + y 2 + 2gx + 2fy + c = 0 …..(i)

Dado que P, Q y R se encuentran en la ecuación (i)

Asi que, 

0 + 00 + 0 + c = 0 …..(ii)

4 + 1 – 4x + 2y + c = 0 …..(iii)

9 + 4 – 6x + 4y + c = 0 …..(iv)

Ahora, al resolver las ecuaciones (ii), (iii) y (iv), obtenemos,

g = -3/2, f = -11/2 y c = 0

Ahora ponga todos estos valores en la ecuación (i), obtenemos

la ecuacion del circulo es

x2 + y2 – 3x – 11y = 0

Pregunta 3. Encuentra la ecuación del círculo que pasa por (3, -2), (-2, 0) y tiene su centro en la recta 2x – y = 3.

Solución:

Se da que, la circunferencia que pasa por P(3, -2) y Q(-2, 0) y tiene su centro en 2x – y = 3.

Como sabemos que la ecuación general de las circunferencias es

x 2 + y 2 + 2gx + 2fy + c = 0 …..(i)

Como el círculo pasa por (3, -2) y también por (-2, 0) 

Asi que, 

9 + 4 + 6g – 4f + c = 0 …..(ii)

4 + 0 – 4g + 0 + c = 0 …..(iii)

Además, el centro del círculo se encuentra en 2x – y = 3

-2g + f = 3 …..(iv)

Ahora, al resolver las ecuaciones (ii), (iii) y (iv), obtenemos,

g = 3/2, f = 6 y c = 2

Ahora ponga todos estos valores en la ecuación (i), obtenemos

la ecuacion del circulo es

x2 + y2 + 3x + 12y + 2 = 0

Pregunta 4. Encuentra la ecuación del círculo que pasa por los puntos (3, 7), (5, 5), y tiene su centro en la recta x – 4y = 1.

Solución:

Se da que, la circunferencia que pasa por P(3, 7) y Q(5, 5) y tiene su centro en x – 4y = 1

Como sabemos que la ecuación general de las circunferencias es

x 2 + y 2 + 2gx + 2fy + c = 0 …..(i)

Como el círculo pasa por P y Q

asi que, 

9 + 49 + 7g + 14f + c = 0 …..(ii)

25 + 25 + 10g + 10f + c = 0 …..(iii)

Además, el centro del círculo se encuentra en x – 4y = 1

entonces, -g + 4f = 1 …..(iv)

Ahora, al resolver las ecuaciones (ii), (iii) y (iv), obtenemos,

g = 3, f = 1 y c = -90

Ahora ponga todos estos valores en la ecuación (i), obtenemos

la ecuacion del circulo es  

x2 + y2 + 6x + 2y – 90 = 0

Pregunta 5. Demuestre que los puntos (3, -2), (1, 0), (-1, -2) y (1, -4) son concíclicos.

Solución:

Dado que P (3, -2), Q (1, 0), R (-1, -2) y S (1, -4)

Como sabemos que la ecuación general de las circunferencias es

x 2 + y 2 + 2gx + 2fy + c = 0 …..(i)

Como el círculo pasa por P, Q y R

Asi que, 

9 + 4 + 6g – 4f + c = 0 …..(ii)

1 + 0 + 2g – 0 + c = 0 …..(iii)

1 + 4 – 2g – 4f + c = 0 …..(iv)

Ahora, al resolver las ecuaciones (ii), (iii) y (iv), obtenemos,

g = -1, f = 2 y c = 1

Ahora ponga todos estos valores en la ecuación (i), obtenemos

la ecuacion del circulo es  

x 2 + y 2 – 2x + 4y + 1 = 0 …..(v)

Aquí vemos claramente que el punto S(1,-4) satisface la ecuación (v)

Por lo tanto, los puntos P, Q, R y S son concíclicos  

Pregunta 6. Muestre que los puntos (5, 5), (6, 4), (-2, 4) y (7, 1) se encuentran todos en un círculo y encuentre su ecuación, centro y radio.

Solución:

Como sabemos que la ecuación general de las circunferencias es

x 2 + y 2 + 2gx + 2fy + c = 0 …..(i)

Centro = (-g, -f)

Radio = \sqrt{g^2+f^2-c}

Por lo tanto, P(5, 5), Q(6, 4) y R(-2, 4) se encuentran en la ecuación (i), 

Asi que, 

25 + 25 + 10g + 10f + c = 0 …..(ii)

36 + 16 + 12g + 8f + c = 0 …..(iii)

4 + 16 + 4g + 8f + c = 0 …..(iv)

Ahora, al resolver las ecuaciones (ii), (iii) y (iv), obtenemos,

g = -2, f = -1, c = -20

Ahora ponga todos estos valores en la ecuación (i), obtenemos

la ecuacion del circulo es  

x 2 + y 2 – 4x – 2y – 20 = 0 …..(v)

Aquí vemos claramente que el punto S(7, 1)

Por lo tanto, los puntos P, Q, R y S son concíclicos  

Ahora, el centro = (-g, -f) = (2, 1)

Radio = \sqrt{g^2+f^2-c}=\sqrt{4+1+20}=\sqrt{25}=5

Pregunta 7(i). Halla la ecuación de la circunferencia que circunscribe al triángulo formado por las rectas x + y + 3 = 0, x – y + 1 = 0 y x = 3.

Solución:

Las ecuaciones de las rectas son

x + y = -3 …..(yo)

x – y = -1 …..(ii)

x = 3 …..(iii)

Consideremos que A, B y C son el punto de intersección de las líneas (i), (ii) y (iii)

Entonces, Punto A(-2,-1), B(3, 4) y C(3,-6)

Como sabemos que la ecuación general de las circunferencias es

x 2 + y 2 + 2gx + 2fy + c = 0 …..(iv)

Entonces, el círculo que circunscribe el ∆ABC

4 + 1 – 4g – 2f + c = 0 …..(v)

9 + 16 + 6g + Bf + c = 0 …..(vi)

9 + 36 + 6g – 12f + c = 0 …..(vii)

Ahora, al resolver las ecuaciones (v), (vi) y (vii), obtenemos,

g = -3, f = 1, c = -15

Ahora ponga todos estos valores en la ecuación (iv), obtenemos

la ecuacion del circulo es  

x2 + y2 – 6x + 2y – 15 = 0

Pregunta 7(ii). Halla la ecuación de la circunferencia que circunscribe al triángulo formado por las rectas 2x + y – 3 = 0, x + y – 1 = 0 y 3x + 2y – 5 = 0.

Solución:

Las ecuaciones de las rectas son

2x + y = 3 …..(yo)

x + y = 1 …..(ii)

3x + 3y = 5 …..(iii)

Consideremos que A, B y C son el punto de intersección de las líneas (i), (ii) y (iii)

Entonces, A = (2, -1)

B = (3, -2)

C = (1, 1)

Como sabemos que la ecuación general de las circunferencias es

x 2 + y 2 + 2gx + 2fy + c = 0 …..(iv)

Entonces, el círculo que circunscribe el ∆ABC

4 + 1 + 4g – 2f + c = 0 …..(v)

9 + 4 + 6g – 4f + c = 0 …..(vi)

1 + 1 + 2g + 2f + c = 0 …..(vii)

Ahora, al resolver las ecuaciones (v), (vi) y (vii), obtenemos,

g = -13/2, f = -5/2 y c = 16

Ahora ponga todos estos valores en la ecuación (iv), obtenemos

la ecuacion del circulo es  

x2 + y2 – 13x – 5y + 16 = 0

Pregunta 7(iii). Halla la ecuación de la circunferencia que circunscribe al triángulo formado por las rectas x + y = 2, 3x – 4y = 6 y x – y = 0.

Solución:

Las ecuaciones de las rectas son

x + y = 2 …..(yo)

3x – 4y = 6 …..(ii)

x – y = 0 …..(iii)

Consideremos que A, B y C son el punto de intersección de las líneas (i), (ii) y (iii)

Entonces, A = (2, 0)

B = (-6, -6)

C = (1, 1)

Como sabemos que la ecuación general de las circunferencias es

x 2 + y 2 + 2gx + 2fy + c = 0 …..(iv)

Entonces, el círculo que circunscribe el ∆ABC

4 + 4g + c = 0 …..(v)

36 + 36 – 12g – 12f + c = 0 …..(vi)

1 + 1 + 2g + 2f + c = 0 …..(vii)

Ahora, al resolver las ecuaciones (v), (vi) y (vii), obtenemos,

g = 2, f = 3 y c = -12

Ahora ponga todos estos valores en la ecuación (iv), obtenemos

la ecuacion del circulo es  

x2 + y2 + 4x + 6y – 12 = 0

Pregunta 7(iv). Halla la ecuación de la circunferencia que circunscribe al triángulo formado por las rectas y = x + 2, 3y = 4x y 2y = 3x.

Solución:

Las ecuaciones de las rectas son

y = x + 2 …..(yo)

3y = 4x …..(ii)

2y = 3x …..(iii)

Consideremos que A, B y C son el punto de intersección de las líneas (i), (ii) y (iii)

Entonces, A = (6, 8)

B = (4, 6)

C = (0, 0)

Como sabemos que la ecuación general de las circunferencias es

x 2 + y 2 + 2gx + 2fy + c = 0 …..(iv)

Entonces, el círculo que circunscribe el ∆ABC

12g + 16f + c = -100 …..(v)

8g + 12f + c = -52 …..(vi)

c = 0 …..(vii)

Ahora, al resolver las ecuaciones (v), (vi) y (vii), obtenemos,

f = 11 y g = -23

Ahora ponga todos estos valores en la ecuación (iv), obtenemos

la ecuacion del circulo es  

x2 + y2 – 46x + 22y = 0.

Pregunta 8. Demuestra que el centro de los tres círculos x 2 + y 2 – 4x – 6y – 12 = 0, x 2 + y 2 + 2x + 4y – 10 = 0, y x 2 + y 2 -10x – 16y – 1 = 0 son colineales.

Solución:

Las ecuaciones dadas de los círculos son,

x 2 + y 2 – 4x – 6y – 12 = 0 …….(i)

x 2 + y 2 + 2x + 4y – 10 = 0 …….(ii)

x 2 + y 2 – 10x – 16y – 1 = 0 …….(iii)

Sean O1, O2 y O3 los centros de (i), (ii) y (iii)

O1 = (-g, -f) = (2, 3)

O2 = (-g, -f) = (-1, -2)

O3 = (-g, -f) = (5, 8)

 O1, O2 y O3 serán colineales si ar(∆ O1O2O3) = 0

ar(∆ O1O2O3)=\frac{1}{2} \begin{vmatrix} x_1 & y_1 & 1\\ x_2 & y_2 & 1\\ x_3 & y_3 & 1 \end{vmatrix}

=\frac{1}{2} \begin{vmatrix} 2 & 3 & 1\\ -1 & -2 & 1 \\ 5 & 8 & 1 \end{vmatrix}=\frac{1}{2} \begin{vmatrix} 2 & 3 & 1\\ -3 & -5 & 0 \\ 3 & 5 & 0 \end{vmatrix}

R2 ⇒ R2 ⇒ -R1

R3 ⇒ R3 ⇒ -R1

=\frac{1}{2} \begin{vmatrix} 2 & 3 & 1\\ -1 & -2 & 1 \\ 5 & 8 & 1 \end{vmatrix}=\frac{1}{2} \begin{vmatrix} 2 & 3 & 1\\ -3 & -5 & 0 \\ 3 & 5 & 0 \end{vmatrix}

O1, O2 y O3 son colineales

Pregunta 9. Demuestra que los radios de los círculos x 2 + y 2 = 1, x 2 + y 2 – 2x – 6y – 6 = 0, y x 2 + y 2 – 4x – 12y – 9 = 0 están en AP

Solución:

Las ecuaciones dadas de los círculos son,

x 2 + y 2 = 1 ———–(i)

x 2 + y 2 – 2x – 6y – 6 = 0 ———-(ii)

x 2 + y 2 – 4x – 12y – 9 = 0 ———-(iii)

Consideremos que R1, R2 y R3 son los radios de (i), (ii) y (iii)

Entonces, R1 = 1

R2 = \sqrt{g^2+f^2-c}=\sqrt{1^2+3^2+6}=\sqrt{16}=4

R3 = \sqrt{g^2+f^2-c}=\sqrt{2^2+6^2+9}=\sqrt{49}=7          

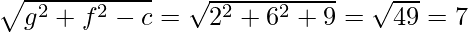
Como sabemos que si a, b, c están en AP, entonces b = a + b/2   

entonces, a = 1, b = 4, c = 7, b = 1 + 7/2 = 4 

Por lo tanto 1, 4, 7 están en AP. 

Por lo tanto, el radio de los tres círculos está en AP.

Pregunta 10. Encuentra la ecuación del círculo que pasa por el origen y corta la cuerda de longitud 4 y 6 en el lado positivo del eje x y el eje y respectivamente.

Solución:

Se da que una circunferencia que pasa por el origen O(0, 0) y 

corte en las intersecciones de longitud 4 en el eje x y 6 en el eje y.

Entonces, OA = 4

BO = 6

Supongamos que C es el centro del círculo y 

CM y CN son líneas perpendiculares dibujadas en OA y OB 

entonces, la coordenada de A = (4, 0) y B = (0, 6)

Las coordenadas de M = (2, 0) y N = (0, 3)

Y las coordenadas de C = (2, 3)

Ahora en ∆OCM, 

Usando el teorema de Pitágoras

OC 2 = OM 2 + CM 2

= 22 + 32                    

= 4 + 9

CO = √13

Por lo tanto, el círculo requerido es

(x-2) 2 + (y-3) 2 = 13

x2 + y2 – 4x – 6y = 0

Pregunta 11. Encuentra la ecuación del círculo concéntrico con círculos x 2 + y 2 – 6x + 12y + 15 = 0 y el doble de su área.

Solución:

La ecuación dada del círculo es

x 2 + y 2 – 6x + 12y + 15 = 0 …….(i)

entonces, centro = (-g, -f) = (3, 6)

radio = \sqrt{g^1+f^2-c}=\sqrt{9+36-15}=\sqrt{30}

Ahora, la ecuación requerida del círculo en concéntrico con (i) 

eso significa que ambos tienen el mismo centro (3,-6)

El área del círculo requerido = 2 * Área de (i)

πR 2 = 2 * π(√30) 2

R2 = 60

R = 2√15

Por lo tanto, el círculo requerido es

(x – 3) 2 + (y + 6) 2 = 60

x2 + y2 – 6x + 12y – 15 = 0

Pregunta 12. Encuentra la ecuación del círculo que pasa por los puntos (1, 1), (2, 2), y cuyo radio es 1. Demuestra que hay dos círculos de este tipo.

Solución:

Como sabemos que la ecuación general de las circunferencias es

x 2 + y 2 + 2gx + 2fy + c = 0 …..(i)

Se da que los puntos P(1, 1) y Q(2, 2) pasan por la eq(1)

Asi que, 

1 + 1 + 2g + 2f + c = 0 …..(ii)

4 + 4 + 4g + 4f + c = 0 …..(iii)

Se da que el radio = 1

⇒\sqrt{g^2+f^2-c}=1

⇒ g 2 + f2 – c = 1 ……(iv)

Ahora de la ecuación (ii) y (iii), obtenemos

sol + f + c/2 = -1  

sol + f + c/4 = -2

Ahora al restar ambas ecuaciones, obtenemos

c = 4

g + f = -3 …….(v)

Ahora, al resolver las ecuaciones (v) y (vi), obtenemos

g = -1 o -2 y f = -2 o -1

Por lo tanto, el círculo requerido es

x2 + y2 – 2x – 4y + 4 = 0

o 

x2 + y2 – 4x – 2y + 4 = 0

Pregunta 13. Encuentra la ecuación del círculo concéntrico con x 2 + y 2 – 4x – 6x – 6y – 3 = 0 y que toca el eje y.

Solución:

La ecuación dada del círculo es  

x 2 + y 2 – 4x – 6y – 3 = 0 …..(i)

entonces, centro = (-g, -f) = (2, 3)

El círculo requerido es concéntrico con eq(i) 

entonces, ambos tienen centro (2, 3)

 Además, el círculo requerido toca el eje y en A.

Entonces, CA = radio = 2

Por lo tanto, el círculo requerido es

(x-2) 2 + (y-3) 2 = 4

x2 + y2 – 4x – 6y + 9 = 0

Pregunta 14. Si un círculo pasa por el punto (0, 0), (a, 0), (0, b), entonces encuentre las coordenadas de su centro.

Solución:

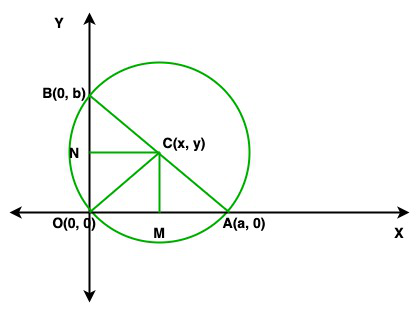
De la figura dada, CA, CO y AB son los radios iguales del círculo 

Asi que, 

CA = CO = CB = r

Además, OCA es un triángulo isósceles y CM es la bisectriz perpendicular a OA.

Por lo tanto OM = a/2

De manera similar, CN es la bisectriz perpendicular a OB

Entonces, ENCENDIDO = b/2

de la figura anterior, es claro que

OM = x = a/2

ENCENDIDO = y = b/2

Por lo tanto, el centro del círculo es c(a/2, b/2)  

Pregunta 15. Encuentra la ecuación del círculo que pasa por el punto (2, 3) y (4, 5), y el centro se encuentra en la línea recta y – 4x + 3 = 0.

Solución:

Se da que una circunferencia que pasa por el punto P(2, 3) y Q(4, 5) y 

el centro está en la línea recta y – 4x + 3 = 0.

Como sabemos que la ecuación general de las circunferencias es

x 2 + y 2 + 2gx + 2fy + c = 0 …..(i)

Como el círculo pasa por P, y Q

Asi que, 

13 + 14g + 6f + c = 0 …..(ii)

41 + 8g + 10f + c = 0 …..(iii)

Centro (-g, -f) se encuentra en y – 4x + 3 = 0

Entonces, -f + 4g = -3 …..(iv)

Ahora, al restar la ecuación (ii) de (iii), obtenemos

28 + 4g + 4f = 0 …..(v)

Al resolver las ecuaciones (iv) y (v) obtenemos,

f = -5 y g = -2

Ahora ponga todos estos valores en la ecuación (i), obtenemos

la ecuacion del circulo es  

41 – 16 – 50 + c = 0

c = 25

Por lo tanto, la ecuación requerida del círculo es,

x2 + y2 – 4x – 10y + 25 = 0

Publicación traducida automáticamente

Artículo escrito por ysachin2314 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *