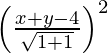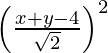Clase 11 Soluciones RD Sharma – Capítulo 25 Parábola – Ejercicio 25.1

Pregunta 11. Encuentra la ecuación de la parábola cuyo foco es (5, 2) y que tiene un vértice en (3, 2).

Solución:

Dado que, el vértice de la parábola es (3, 2) y el foco de la parábola es (5, 2)

Entonces, la pendiente del eje de la parábola = 0

La pendiente de la directriz no está definida.

Supongamos que la directriz corta el eje en el punto K (r, s).

Entonces, (r + 5)/2 = 3, (s + 2)/2 = 2

=> r = 1, s = 2

Por lo tanto, la ecuación de la directriz es x – 1 = 0 o x = 1.

Ahora, supongamos que P (x, y) sea cualquier punto de la parábola cuyo foco sea S (5, 2).

Y la ecuación de la directriz es x =1.

Entonces, primero dibujamos PM perpendicular a x = 1.

Después

SP = P.M.

SP ² = PM ²

(x – 5) ² + (y – 2) ² = $\left( \frac{x - 1}{1} \right)^2$

x2 ⁺ 25 – 10x + y2 ⁺ 4 – 4y = x2 + ¹ – 2x

25 – 10x + y ² + 4 – 4y – 1 + 2x = 0

=> y ² – 4y – 8x + 28 = 0

Por lo tanto, la ecuación de la parábola es y ² – 4y – 8x + 28 = 0

Pregunta 12. El cable de un puente colgante cargado uniformemente cuelga en forma de parábola. La calzada que es horizontal y de 100 m de largo está sostenida por alambres verticales unidos al cable, siendo el alambre más largo de 30 my el más corto de 6 m. Encuentre la longitud de un cable de soporte unido a la calzada a 18 m del centro.

Solución:

Dado que el cable de suspensión forma una parábola con el vértice en (0, 6).

Entonces, supongamos que la ecuación de la parábola formada por el cable de suspensión sea,

(x – 0) ² = 4a (y – 6)

Y pasa por el punto P (−50, 30) y Q (50, 30).

Entonces, 2500 = 4a (30 – 6)

=> 4a = 2500/24

Poniendo el valor de 4a en la ecuación dada, obtenemos

x2 ⁼ (2500/24) (y – 6)

Ahora, sean las coordenadas (18, l) y se encuentra en la parábola (2).

Entonces, 18 ² = (2500/24) (l – 6)

=> 324 = (2500/24) (l – 6)

=> largo = 9,11 metros

Por lo tanto, 9,11 m es el cable de soporte unido a la calzada a 18 m del medio.

Pregunta 13. Hallar las ecuaciones de las rectas que unen el vértice de la parábola y ² = 6x con el punto de abscisa 24.

Solución:

Supongamos que A y B son puntos en la parábola y ² = 6x.

Ahora bien, sean OA, OB las rectas que unen el vértice O con los puntos A y B cuya abscisa es 24.

Ahora,

=> y ² = 6 × 24

=> y2 ⁼ 144

=> y = ± 12

Entonces, las coordenadas de los puntos A son (24, 12) y B es (24, –12).

Por lo tanto, la ecuación de las rectas es

=> $y - 0 = \pm \frac{12 - 0}{24 - 0}(x - 0)$

=> ±2y = x

Pregunta 14. Encuentra las coordenadas de los puntos en la parábola y ² = 8x cuya distancia focal es 4.

Solución:

Dado que, la parábola es y ² = 8x

⇒ y2 ⁼ 4(2)x

Ahora, al compararla con la ecuación general de la parábola y ² = 4ax, obtendremos a = 2.

Supongamos que el punto requerido sea (x ₁ , y ₁ ).

Además, dado que la distancia focal es 4

=> x ₁ + a = 4

=> x ₁ + 2 = 4

=> x1 = ₂

Ahora, este punto satisface la ecuación de la parábola,

Entonces, (y ₁ ) ² = 8(2) = 16

=> y ₁² = 16

=> y ₁ = ± 4

Por tanto, las coordenadas de los puntos son (2, 4) y (2, −4).

Pregunta 15. Encuentra la longitud del segmento de línea que une el vértice de la parábola y ² = 4ax y un punto en la parábola donde el segmento de línea forma un ángulo θ con el eje x.

Solución:

Supongamos que las coordenadas del punto en la parábola son B (x ₁ , y ₁ ) y BO es el segmento de línea en la parábola.

Ahora, en el triángulo AOB,

cos θ = AO/OB y sen θ = AB/OB

=> cos θ = x ₁ /OB y sen θ = y ₁ /OB

x ₁ = OB cos θ y y ₁ = OB sen θ

Ahora, la curva pasa por el punto (x ₁ , y ₁ )

Entonces, (y ₁ ) ² = 4a(x ₁ )

=> (OB sen θ) ² = 4a (OB cos θ)

=> (OB) ² sen2 θ = 4a OB cos θ

=> OB = 4a cos θ/sen ² θ

=> OB = 4a cosec θ cot θ

Por lo tanto, la longitud requerida es 4a cosec θ cot θ.

Pregunta 16. Si los puntos (0, 4) y (0, 2) son respectivamente el vértice y el foco de una parábola, entonces encuentra la ecuación de la parábola.

Solución:

Dado que el vértice de la parábola es (0, 4) y el foco de la parábola es (0, 2)

De los puntos concluimos que el vértice y el foco se encuentran en el eje y, por lo que el eje y es el eje de la parábola.

Ahora, si la directriz se encuentra con el eje de la parábola en el punto Z, entonces AZ = AF = 2.

OZ = DE + AZ + FA

= 2 + 2 + 2

= 6

Entonces, la ecuación de la directriz es y = 6.

es decir, y − 6 = 0

Supongamos que P(x, y) sea cualquier punto en el plano del foco y la directriz.

Y siendo MP la distancia perpendicular de P a la directriz, entonces P pertenece a la parábola si FP = MP.

$\sqrt{\left( x - 0 \right)^2 + \left( y - 2 \right)^2} = \frac{\left| y - 6 \right|}{1}$

x2 + ^{y2 – 4y}⁺ 4 = ^y2 – 12y + 36

=> x2 ⁺ 8y = 32

Por lo tanto, la ecuación de la parábola es x ² + 8y = 32

Pregunta 17. Si la línea y = mx + 1 es tangente a la parábola y ² = 4x, entonces encuentra el valor de m.

Solución:

Dado que la ecuación de la es y ² = 4x.

Al sustituir el valor de y = mx + 1 en la ecuación de la parábola, obtenemos

(mx + 1) ² = 4x

⇒ metro ² x ² + 2mx + 1 = 4x

⇒ metro ² x ² + (2m − 4)x + 1 = 0

Como sabemos que una tangente toca la curva en un punto, las raíces de la ecuación deben ser iguales.

Entonces, D = 0

=> (2m − 4) ² − 4m ² = 0

=> 4m2 −16m ⁺ 16 − 4m2 = ⁰

=> metro = 1

Por lo tanto, el valor de m es 1.

Pregunta 18. Encuentra la distancia entre el vértice y el foco de la parábola y ² + 6y + 2x + 5 = 0.

Solución:

Dado que la ecuación de la parábola es y ² + 6y + 2x + 5 = 0

(y + 3) ² + 2x – 4 = 0

(y + 3) ² = -2 (x – 2)

Supongamos que Y = y + 3 y X = x – 2.

ahora tenemos

Y ² = – 2X

Al poner 4a = 2, obtenemos

=> un = 1/2

Enfoque = (X = -1/2, Y = 0) = (x = 3/2, y = – 3)

Vértice = (X = 0, Y = 0) = (x = 2, y = -3)

Asi que,

Enfoque = (3/2, -3)

Vértice = (2, -3)

Ahora, encontramos que la distancia entre el vértice y el foco es,

re = $\sqrt{\left( \frac{3}{2} - 2 \right)^2 + \left( - 3 + 3 \right)^2}$

= $\sqrt{\left( \frac{1}{2} \right)^2}$

= 1/2 unidades

Por lo tanto, la distancia requerida es 1/2 unidades.

Pregunta 19. Encuentra la ecuación de la directriz de la parábola x ² − 4x − 8y + 12 = 0.

Solución:

Dado que la ecuación de la parábola es x ² − 4x − 8y + 12 = 0

(x – 2) ² – 4 – 8y + 12 = 0

(x-2) ² = 8 (y-1)

Supongamos que Y = y − 1 y X = x – 2.

ahora tenemos

X2 ⁼ 8Y

Ahora, al comparar con x ² = 4ay, obtenemos

=> un = 2

Entonces, Directriz = Y = −a

=> y − 1 = −a

=> y = −a + 1

=> y = −2 + 1

=> y = −1

Por lo tanto, la ecuación requerida de la directriz es y = -1.

Pregunta 20. Escribe la ecuación de la parábola con foco (0, 0) y directriz x + y − 4 = 0.

Solución:

Dado que el foco (0, 0) y la directriz x + y − 4 = 0 de la parábola

Ahora, supongamos que P (x, y) sea cualquier punto de la parábola con el foco y la directriz dados

Entonces, primero dibujamos PM perpendicular a x + y = 4.

Después,

SP = P.M.

SP ² = PM ²

(x – 0) ² + (y – 0) ² = $\left( \frac{x + y - 4}{\sqrt{1 + 1}} \right)^2$

x ² + y ² = $\left( \frac{x + y - 4}{\sqrt{2}} \right)^2$

2x ² + 2y ² = x ² + y ² + 16 + 2xy – 8y – 8x

=> x2 + ^{y2 –}^2xy + 8x + 8y – 16 = 0

Por lo tanto, la ecuación de la parábola es x ² + y ² – 2xy + 8x + 8y – 16 = 0

Publicación traducida automáticamente

Artículo escrito por prabhjotkushparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 11 Soluciones RD Sharma – Capítulo 25 Parábola – Ejercicio 25.1 | conjunto 2

Pregunta 11. Encuentra la ecuación de la parábola cuyo foco es (5, 2) y que tiene un vértice en (3, 2).

Pregunta 13. Hallar las ecuaciones de las rectas que unen el vértice de la parábola y ² = 6x con el punto de abscisa 24.

Pregunta 14. Encuentra las coordenadas de los puntos en la parábola y ² = 8x cuya distancia focal es 4.

Pregunta 15. Encuentra la longitud del segmento de línea que une el vértice de la parábola y ² = 4ax y un punto en la parábola donde el segmento de línea forma un ángulo θ con el eje x.

Pregunta 16. Si los puntos (0, 4) y (0, 2) son respectivamente el vértice y el foco de una parábola, entonces encuentra la ecuación de la parábola.

Pregunta 17. Si la línea y = mx + 1 es tangente a la parábola y ² = 4x, entonces encuentra el valor de m.

Pregunta 18. Encuentra la distancia entre el vértice y el foco de la parábola y ² + 6y + 2x + 5 = 0.

Pregunta 19. Encuentra la ecuación de la directriz de la parábola x ² − 4x − 8y + 12 = 0.

Pregunta 20. Escribe la ecuación de la parábola con foco (0, 0) y directriz x + y − 4 = 0.

Deja una respuesta Cancelar la respuesta

Pregunta 11. Encuentra la ecuación de la parábola cuyo foco es (5, 2) y que tiene un vértice en (3, 2).

Pregunta 13. Hallar las ecuaciones de las rectas que unen el vértice de la parábola y 2 = 6x con el punto de abscisa 24.

Pregunta 14. Encuentra las coordenadas de los puntos en la parábola y 2 = 8x cuya distancia focal es 4.

Pregunta 15. Encuentra la longitud del segmento de línea que une el vértice de la parábola y 2 = 4ax y un punto en la parábola donde el segmento de línea forma un ángulo θ con el eje x.

Pregunta 16. Si los puntos (0, 4) y (0, 2) son respectivamente el vértice y el foco de una parábola, entonces encuentra la ecuación de la parábola.

Pregunta 17. Si la línea y = mx + 1 es tangente a la parábola y 2 = 4x, entonces encuentra el valor de m.

Pregunta 18. Encuentra la distancia entre el vértice y el foco de la parábola y 2 + 6y + 2x + 5 = 0.

Pregunta 19. Encuentra la ecuación de la directriz de la parábola x 2 − 4x − 8y + 12 = 0.

Pregunta 20. Escribe la ecuación de la parábola con foco (0, 0) y directriz x + y − 4 = 0.

Deja una respuesta Cancelar la respuesta

Pregunta 13. Hallar las ecuaciones de las rectas que unen el vértice de la parábola y ² = 6x con el punto de abscisa 24.

Pregunta 14. Encuentra las coordenadas de los puntos en la parábola y ² = 8x cuya distancia focal es 4.

Pregunta 15. Encuentra la longitud del segmento de línea que une el vértice de la parábola y ² = 4ax y un punto en la parábola donde el segmento de línea forma un ángulo θ con el eje x.

Pregunta 17. Si la línea y = mx + 1 es tangente a la parábola y ² = 4x, entonces encuentra el valor de m.

Pregunta 18. Encuentra la distancia entre el vértice y el foco de la parábola y ² + 6y + 2x + 5 = 0.

Pregunta 19. Encuentra la ecuación de la directriz de la parábola x ² − 4x − 8y + 12 = 0.