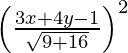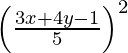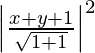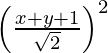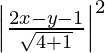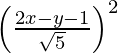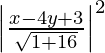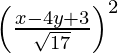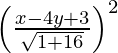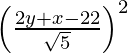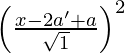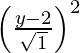Clase 11 Soluciones RD Sharma – Capítulo 25 Parábola – Ejercicio 25.1

Pregunta 1. Encuentra la ecuación de la parábola cuya:

(i) El foco es (3, 0) y la directriz es 3x + 4y = 1

Solución:

Dado que el foco es (3, 0) y la directriz es 3x + 4y = 1

Supongamos que P (x, y) sea cualquier punto de la parábola.

Entonces, primero dibujamos PM perpendicular a 3x + 4y = 1.

Después,

SP = P.M.

SP ² = PM ²

(x – 3) ² + (y – 0) ² = $\left( \frac{3x + 4y - 1}{\sqrt{9 + 16}} \right)^2$

(x – 3) ² + y ² = $\left( \frac{3x + 4y - 1}{5} \right)^2$

25 (x ² + 9 – 6x + y ² ) = (3x + 4y – 1) ²

25x ² – 150x + 25y ² + 225 = 9x ² + 16y ² + 1 + 24xy – 8y – 6x

=> 16x ² + 9y ² – 24xy – 144x + 8y + 224 = 0

Por lo tanto, la ecuación de la parábola es 16x ² + 9y ² – 24xy – 144x + 8y + 224 = 0

(ii) El foco es (1, 1) y la directriz es x + y + 1 = 0

Solución:

Dado que el foco es (1, 1) y la directriz es x + y + 1 = 0

Supongamos que P (x, y) sea cualquier punto de la parábola.

Entonces, primero dibujamos PM perpendicular a x + y + 1 = 0.

Después,

SP = P.M.

SP ² = PM ²

(x-1) ² + (y-1) ² = $\left| \frac{x + y + 1}{\sqrt{1 + 1}} \right|^2$

(x-1) ² + (y-1) ² = $\left( \frac{x + y + 1}{\sqrt{2}} \right)^2$

2 (x ² + 1 – 2x + y ² + 1 – 2y) = x ² + y ² + 1 + 2xy + 2y + 2x

(2x ² + 2 – 4x + 2 y ² + 2 – 4y) = x ² + y ² + 1 + 2xy + 2y + 2x

=> x2 ⁺ y2 ^– 2xy – 6x – 6y + 3 = 0

Por lo tanto, la ecuación de la parábola es x ² + y ² – 2xy – 6x – 6y + 3 = 0

(iii) El foco es (0, 0) y la directriz 2x − y − 1 = 0

Solución:

Dado que el foco es (0, 0) y la directriz 2x − y − 1 = 0

Supongamos que P (x, y) sea cualquier punto de la parábola.

Entonces, primero dibujamos PM perpendicular a 2x − y − 1 = 0.

Después,

SP = P.M.

SP ² = PM ²

(x – 0) ² + (y – 0) ² = $\left| \frac{2x - y - 1}{\sqrt{4 + 1}} \right|^2$

x ² + y ² = $\left( \frac{2x - y - 1}{\sqrt{5}} \right)^2$

5x ² + 5 y ² = 4x ² + y ² + 1 – 4xy + 2y – 4x

=> x ² + 4y ² + 4xy – 2y + 4x – 1 = 0

Por lo tanto, la ecuación de la parábola es x ² + 4y ² + 4xy – 2y + 4x – 1 = 0

(iv) El foco es (2, 3) y la directriz x − 4y + 3 = 0.

Solución:

Dado que el foco es (2, 3) y la directriz x − 4y + 3 = 0

Supongamos que P (x, y) sea cualquier punto de la parábola.

Entonces, primero dibujamos PM perpendicular a x − 4y + 3 = 0.

Después,

SP = P.M.

SP ² = PM ²

(x-2) ² + (y-3) ² = $\left| \frac{x - 4y + 3}{\sqrt{1 + 16}} \right|^2$

(x-2) ² + (y-3) ² = $\left( \frac{x - 4y + 3}{\sqrt{17}} \right)^2$

17 (x ² + 4 – 4x + y ² – 6y + 9) = x ² + 16y ² + 9 – 8xy – 24y + 6x

17x ² – 68x – 102y + 17y ² + 13 (17) = x ² + 16y ² + 9 – 8xy – 24y + 6x

=> 16x ² + y ² + 8xy – 74x – 78y + 212 = 0

Por lo tanto, la ecuación de la parábola es 16x ² + y ² + 8xy – 74x – 78y + 212 = 0

Pregunta 2. Encuentra la ecuación de la parábola cuyo foco es el punto (2, 3) y la directriz es la recta x − 4y + 3 = 0. Además, encuentra la longitud de su lado recto.

Solución:

Dado que el foco es (2, 3) y la directriz es la recta x − 4y + 3 = 0.

Supongamos que P (x, y) sea cualquier punto de la parábola.

Entonces, primero dibujamos PM perpendicular a x − 4y + 3 = 0.

Después,

SP = P.M.

SP ² = PM ²

(x-2) ² + (y-3) ² = $\left( \frac{x - 4y + 3}{\sqrt{1 + 16}} \right)^2$

(x-2) ² + (y-3) ² = $\left( \frac{x - 4y + 3}{\sqrt{17}} \right)^2$

17 (x ² + 4 – 4x + y ² – 6y + 9) = x ² + 16y ² + 9 – 8xy – 24y + 6x

17x ² – 68x + 17y ² – 102y + 9 (17) = x ² + 16y ² + 9 – 8xy – 24y + 6x

16x ² + y ² + 8xy – 74x – 78y + 212 = 0

Longitud del latus rectum = 2 (Longitud de la perpendicular desde el foco en la directriz)

= $2\left| \frac{2 - 12 + 3}{\sqrt{16 + 1}} \right|$

= $2\left| \frac{- 7}{\sqrt{17}} \right|$

= $2\left( \frac{7}{\sqrt{17}} \right)$

= 4/√17

Por lo tanto, la longitud de su latus-rectum es 4/√17

Pregunta 3. Encuentra la ecuación de la parábola si

(i) El foco está en (−6, −6) y el vértice está en (−2, 2)

Solución:

Da eso, el foco está en (−6, −6) y el vértice está en (−2, 2)

Supongamos que (x ₁ , y ₁ ) son las coordenadas del punto de intersección del eje y la directriz.

Entonces, la pendiente del eje de la parábola = $\frac{- 6 - 2}{- 6 + 2}$ = -8/-4 = 2

Y la pendiente de la directriz = -1/2

Supongamos que la directriz corta al eje en el punto K (r, s), entonces

(r – 6)/2 = -2, (s – 6)/2 = 2

=> r = 2, s = 10

La ecuación de la directriz es,

y-10 = -1/2 (x-2)

=> 2y + x – 22 = 0

Ahora, supongamos que P (x, y) sea cualquier punto de la parábola

el foco es S (−6, −6).

Y la directriz es 2y + x – 22 = 0.

Entonces, primero dibujamos PM perpendicular a 2x + y + 22 = 0.

Después,

SP = P.M.

SP ² = PM ²

(x + 6) ² + (y + 6) ² = $\left( \frac{2y + x - 22}{\sqrt{5}} \right)^2$

5 (x2 ⁺ 12x + 36 + y2 ⁺ 12y + 36) = 4y2 ⁺ x2 ⁺ 484 + 4xy – 88y – 44x

4x ² + y ² – 4xy + 104x + 148y – 124 = 0

=> (2x – y) ² – 4 (26x + 37y – 31) = 0

Por lo tanto, la ecuación de la parábola es (2x – y) ² – 4 (26x + 37y – 31) = 0

(ii) El foco está en (0, −3) y el vértice está en (0, 0)

Solución:

Dado que el foco está en (0, −3) y el vértice está en (0, 0)

Supongamos que (x ₁ , y ₁ ) son las coordenadas del punto de intersección del eje y la directriz.

Por lo tanto, la pendiente del eje de la parábola no se puede definir.

Entonces, la pendiente de la directriz = 0

Supongamos que la directriz corta el eje en K (r, s).

(r + 0)/2 = 0, (s – 3)/2 = 0

=> r = 0, s = 3

Entonces, la ecuación de la directriz es y = 3

Supongamos que P (x, y) es cualquier punto de la parábola

Con foco es S (0, −3) y la directriz es y = 3.

Entonces, primero dibujamos PM perpendicular a y = 3.

Después,

SP = P.M.

SP ² = PM ²

(x – 0) ² + (y + 3) ² = $\left( \frac{y - 3}{\sqrt{1}} \right)^2$

x2 + y2 ⁺ 6y + 9 = y2 ^–^6y + 9

=> x2 ⁼ -12y

Por lo tanto, la ecuación de la parábola es x ² = -12y

(iii) El foco está en (0, −3) y el vértice está en (−1, −3)

Solución:

Dado que, el foco está en (0, −3) y el vértice está en (−1, −3)

Supongamos que (x ₁ , y ₁ ) son las coordenadas del punto de intersección del eje y la directriz.

Entonces, la pendiente del eje de la parábola es cero y la pendiente de la directriz es

(r + 0)/2 = -1, (s – 3)/2 = – 3

=> r = – 2, s = – 3

La ecuación de la directriz es x + 2 = 0.

Supongamos que P (x, y) es cualquier punto de la parábola cuyo foco es S (0, −3) y la directriz es x + 2 = 0.

Entonces, primero dibujamos PM perpendicular a x + 2 = 0

Después,

SP = P.M.

SP ² = PM ²

(x – 0) ² + (y + 3) ² = $\left| \frac{x + 2}{\sqrt{1}} \right|^2$

x2 + y2 ⁺ 6y + 9 = x2 ⁺^4x + 4

=> y ² + 6y – 4x + 5 = 0

Por lo tanto, la ecuación de la parábola es y ² + 6y – 4x + 5 = 0

(iv) El foco está en (a, 0) y el vértice está en (a’, 0)

Solución:

Dado que el foco está en (a, 0) y el vértice está en (a’, 0)

Supongamos que (x ₁ , y ₁ ) son las coordenadas del punto de intersección del eje y la directriz.

Entonces, la pendiente del eje de la parábola es cero y la pendiente de la directriz no se puede definir.

Supongamos que la directriz corta el eje en el punto K (r, s).

Entonces, (r + a)/2 = a’, (s + 0)/2 = 0

=> r = 2a’ – a, s = 0

La ecuación de la directriz es x – 2a’ + a = 0

Supongamos que P (x, y) es cualquier punto de la parábola

con foco es S (a, 0), y la directriz es x – 2a’ + a = 0.

Entonces, primero dibujamos PM perpendicular a x – 2a’ + a = 0

Después,

SP = P.M.

SP ² = PM ²

(x – a) ² + (y – 0) ² = $\left( \frac{x - 2a' + a}{\sqrt{1}} \right)^2$

y ² = (x – 2a’ + a) ² – (x – a) ²

y2 = ^x2⁺ 4a’2 + a2 ^– 4a’x – 4aa’ + 2ax – ^x2^–^a2 + 2ax

y2 = 4a’2 – ^{4a’x –}^4aa ‘ + 4ax

=> y ² = -4 (a’ – a) (x – a’)

Por lo tanto, la ecuación de la parábola es y ² = -4 (a’ – a) (x – a’)

(v) El foco está en (0, 0) y el vértice está en la intersección de las líneas x + y = 1 y x − y = 3.

Solución:

Dado que el foco está en (0, 0) y el vértice está en la intersección de las líneas x + y = 1 y x − y = 3.

Supongamos que (x ₁ , y ₁ ) son las coordenadas del punto de intersección del eje y la directriz.

Entonces, la pendiente del eje de la parábola = $\frac{- 6 - 2}{- 6 + 2}$ = -8/-4 = 2

Y la pendiente de la directriz = -1/2

Supongamos que la directriz corta el eje en el punto K (r, s).

entonces, (r – 6)/2 = -2, (s – 6)/2 = 2

=> r = 2, s = 10

La ecuación de la directriz es,

y-10 = -1/2 (x-2)

=> 2y + x – 22 = 0

Ahora, supongamos que P (x, y) sea cualquier punto de la parábola

Con foco es S (−6, −6) y la directriz es 2y + x – 22 = 0.

Entonces, primero dibujamos PM perpendicular a 2x + y + 22 = 0.

Después,

SP = P.M.

SP ² = PM ²

(x + 6) ² + (y + 6) ² = $\left( \frac{2y + x - 22}{\sqrt{5}} \right)^2$

5 (x2 ⁺ 12x + 36 + ^y2 + 12y + 36) = 4y2 ⁺ x2 ⁺ 484 + 4xy – 88y – 44x

4x ² + y ² – 4xy + 104x + 148y – 124 = 0

=> (2x – y) ² – 4 (26x + 37y – 31) = 0

Por lo tanto, la ecuación de la parábola es (2x – y) ² – 4 (26x + 37y – 31) = 0

Pregunta 4. Encuentra el vértice, el foco, el eje, la directriz y el latus-rectum de la siguiente parábola:

(i) y ² = 8x

Solución:

Dado que, y ² = 8x

Ahora, al comparar la ecuación dada con y ² = 4ax, obtenemos

=> 4a = 8

=> un = 2

Entonces, el vértice = (0, 0)

Foco = (a, 0) = (2, 0)

La ecuación de la directriz es

x = −a

=> x = −2

Eje = y = 0

Longitud del latus rectum = 4a = 4(2) = 8 unidades

(ii) 4x ² + y = 0

Solución:

Dado que,

4x ² + y = 0

^{=> -y/ 4} = x2

Ahora, al comparar la ecuación dada con x ² = -4ay, obtenemos

=> 4a = 1/4

=> un = 1/16

Entonces, el vértice = (0, 0)

Foco = (0, −a) = (0, -1/16)

Ecuación de la directriz, y = a

=> y = 1/16

Eje = x = 0

Longitud del latus rectum = 4a = 4 (1/16) = 1/4 unidades

(iii) y ² − 4y − 3x + 1 = 0

Solución:

Dado que,

y ² − 4y − 3x + 1 = 0

(y – 2) ² – 4 – 3x + 1 = 0

(y – 2) ² = 3 (x + 1)

(y – 2) ² = 3 (x – (-1))

Supongamos que Y = y – 2 y X = x + 1.

Después,

Y2 ⁼ 3X

Ahora, al comparar la ecuación dada con Y ² = 4aX, obtenemos

=> 4a = 3

=> un = 3/4

Entonces, el vértice = (X = 0, Y = 0) = (x = -1, y = 2)

Enfoque = (X = a, Y = 0) = (x + 1 = 3/4, y – 2 = 0) = (x = -1/4, y = 2)

Ecuación de la directriz: X = −a

es decir, x + 1 = -3/4

=> x = -7/4

Eje = Y = 0

es decir, y – 2 = 0

=> y = 2

Longitud del latus rectum = 4a = 4 (3/4) = 3 unidades

(iv) y ² − 4y + 4x = 0

Solución:

Dado que,

y ² − 4y + 4x = 0

(y – 2) ² – 4 + 4x = 0

(y – 2) ² = -4 (x – 1)

Supongamos que Y = y – 2 y X = x – 1.

Después,

=> Y ² = – 4X

Ahora, al comparar la ecuación dada con Y ² = -4aX, obtenemos

=> 4a = 4

=> un = 1

Entonces, el vértice = (X = 0, Y = 0) = (x = 1, y = 2)

Foco = (X = −a, Y = 0) = (x – 1 = – 1, y – 2 = 0) = (x = 0, y = 2)

Ecuación de la directriz: X = a

es decir, x – 1 = 1

=> x = 2

Eje = Y = 0

es decir, y – 2 = 0

=> y = 2

Longitud del latus rectum = 4a = 4 (1) = 4 unidades

(v) y ² + 4x + 4y − 3 = 0

Solución:

Dado que

y ² + 4y + 4x −3 = 0

(y + 2) ² – 4 + 4x – 3 = 0

(y + 2) ² = – 4 (x – 7/4)

Supongamos que Y = y + 2 y X = x – 7/4

Entonces, Y ² = – 4X.

Ahora, al comparar la ecuación dada con Y ² = -4aX

=> 4a = 4

=> un = 1

Entonces, el Vértice = (X = 0, Y = 0) = (x = 7/4, y = – 2)

Enfoque = (X = −a, Y = 0) = (x – 7/4 = – 1, y + 2 = 0) = (x = 3/4, y = – 2)

Ecuación de la directriz: X = a

es decir, x – 7/4 = 1

=> x = 11/4

Eje = Y = 0

es decir y + 2 = 0

=> y = – 2

Longitud del latus rectum = 4a = 4 (1) = 4 unidades

(vi) ^y2 = 8x + 8y

Solución:

Dado que

y2 ⁼ 8x + 8y

(y – 4) ² = 8 (x + 2)

Al poner Y = y – 4 y X = x + 2, obtenemos

Y2 ⁼ 8X

Al comparar la ecuación dada con Y ² = 4aX, obtenemos

=> 4a = 8

=> un = 2

Entonces, el vértice = (X = 0, Y = 0) = (x = – 2, y = 4)

Enfoque = (X = a, Y = 0) = (x + 2 = 2, y – 4 = 0) = (x = 0, y = 4)

Ecuación de la directriz: X = −a

es decir, x + 2 = – 2

=> x + 4 = 0

Eje = Y = 0

es decir, y – 4 = 0

=> y = 4

Longitud del latus rectum = 4a = 4 (2) = 8 unidades

(vii) 4 (y − 1) ² = − 7 (x − 3)

Solución:

Dado que

4(y − 1) ² = − 7 (x − 3)

(y – 1) ² = -7/4 (x – 3)

Sean Y = y – 1 y X = x – 3.

Después,

Y ² = -7/4 X

Al comparar la ecuación dada con Y ² = – 4aX, obtenemos

=> 4a = 7/4

=> un = 7/16

Entonces, el vértice = (X = 0, Y = 0) = (x = 3, y = 1)

Foco = (X = −a, Y = 0) = (x – 3 = -7/16, y – 1 = 0) = (x = 41/16, y = 1)

Ecuación de la directriz: X = a

es decir, x – 3 = 7/16

=> x = 55/16

Eje = Y = 0

es decir, y – 1 = 0

=> y = 1

Longitud del latus rectum = 4a = 4 (7/16) = 7/4 unidades

(viii) y ² = 5x − 4y − 9

Solución:

Dado que,

y ² = 5x − 4y − 9

y ² + 4y = 5x – 9

(y + 2) ² = 5x – 5

(y + 2) ² = 5 (x – 1)

Al poner Y = y + 2 y X = x – 1, obtenemos

Y2 ⁼ 5X

Al comparar la ecuación dada con Y ² = 4aX, obtenemos

=> 4a = 5

=> un = 5/4

Entonces el vértice = (X = 0, Y = 0) = (x = 1, y = -2)

Foco = (X = a, Y = 0) = (x – 1 = 5/4, y + 2 =0) = (x = 9/4, y = -2)

Ecuación de la directriz: X = −a

es decir, x – 1 = -5/4

=> x = -1/4

Eje = Y = 0

es decir y + 2 = 0

=> y = – 2

Longitud del latus rectum = 4a = 4 (5/4) = 5 unidades

(ix) x ² + y = 6x − 14

Solución:

Dado que

x2 ⁼ 6x − y − 14

(x – 3) ² = -y – 14 + 9

(x – 3) ² = -y – 5

(x – 3) ² = – (y + 5)

Supongamos que Y = y + 5 y X = x – 3.

Después,

X2 ⁼ – Y

Al comparar la ecuación dada con X ² = – 4aY, obtenemos

=> 4a = 1

=> un = 1/4

Entonces, el vértice = (X = 0, Y = 0) = (x = 3, y = – 5)

Foco = (X = 0, Y = −a) = (x – 3 = 0, y + 5 = -1/4) = (x = 3, y = -21/4)

Ecuación de la directriz: Y = a

es decir y + 5 = 1/4

=> y = -19/4

Eje = X = 0

es decir, x – 3 = 0

=> x = 3

Longitud del latus rectum = 4a = 4 (1/4) = 1 unidades

Pregunta 5. Para la parábola, y ² = 4px encuentra los extremos de una ordenada doble de longitud 8p. Demostrar que las líneas desde el vértice hasta sus extremos son ángulos rectos.

Solución:

Dado que la ecuación de la parábola es y ² = 4px.

Supongamos que PQ es la coordenada doble de longitud 8p de la parábola y sea A el vértice de la parábola.

y2 ⁼ 4px

Después,

RP = RQ = 4p

Sea AR = x ₁

Entonces, las coordenadas de P y Q son (x ₁ , 4p) y (x ₁ , -4p)

Ahora, P se encuentra en y ² = 4px.

Entonces, (4p) ² = 4p x ₁

=> x ₁ = 4p

Entonces, las coordenadas de P son (4p, 4p) y Q son (4p, -4p)

Las coordenadas de A son (0, 0).

Entonces, m ₁ = Pendiente de AP = $\frac{4p - 0}{4p - 0}$ = 4p/4p = 1

Y, m ₂ = Pendiente de AQ = $\frac{\left( - 4p - 0 \right)}{4p - 0}$ = -4p/4p = -1

Ahora,

metro ₁ metro ₂ = – 1

Por tanto, AP es perpendicular a AQ.

Por lo tanto probado.

Pregunta 6. Halla el área del triángulo formado por las rectas que unen el vértice de la parábola x ² = 12y con los extremos de su latus rectum.

Solución:

Dado que la ecuación de la parábola es x ² = 12y.

Ahora al comparar la ecuación dada con x ² = 4ay, obtenemos

=> 4a = 12

=> un = 3

Entonces, las coordenadas del foco son (0, 3).

Ahora dos puntos se encuentran en la parábola.

=> x2 = ¹² (3)

=>x2 = ³⁶

=> x = ±6

Por lo tanto, los puntos son P (6, 3) y Q (-6, 3).

Distancia PQ = $\sqrt{(6 - (-6))^2 + (3 - 3)^2}$

= $\sqrt{(6 + 6)^2 + (3 - 3)^2}$

= $\sqrt{(12)^2 + (0)^2}$

= 12

Área = (PQ) (3) (1/2)

= (12) (3) (1/2)

= 18 unidades cuadradas

Por tanto, el área del triángulo formado por las rectas que unen el vértice de la parábola dada con los extremos de su lado recto es de 18 unidades cuadradas.

Pregunta 7. Encuentra las coordenadas del punto de intersección del eje y la directriz de la parábola cuyo foco es (3, 3) y la directriz es 3x − 4y = 2. Encuentra también la longitud del latus-rectum.

Solución:

Dado que la ecuación de la directriz es 3x − 4y = 2.

Entonces, la pendiente de la directriz = -3/-4 = 3/4

El eje es perpendicular a la directriz.

entonces, la pendiente del eje = -4/3

Ahora, el foco está en el eje de la parábola.

Entonces, la ecuación del eje es

=> y – 3 = (-4/3) (x – 3)

=> 3y – 9 = -4x + 12

=> 3y + 4x – 21 = 0

Al resolver las ecuaciones (1) y (2), obtenemos

x = 18/5, y = 11/5

Entonces, el punto de intersección del eje y la directriz es (18/5, 11/5).

Ad la longitud del latus rectum = 2 (Longitud de la perpendicular desde el foco en la directriz)

= $2\left| \frac{3\left( 3 \right) + \left( - 4 \right)3 - 2}{\sqrt{16 + 9}} \right|$

= $2\left| \frac{- 5}{\sqrt{16 + 9}} \right|$

= 2

Pregunta 8. ¿En qué punto de la parábola x ² = 9y la abscisa es el triple de la coordenada?

Solución:

Tenemos,

=> x2 ⁼ 9y

Ahora, al poner x = 3y en la ecuación dada de la parábola, obtenemos

=> 9 años ² = 9 años

=> 9y (y – 1) = 0

=> y = 0, 1

En y = 0, x = 0.

Y también en y = 1, x = 3.

Por lo tanto, en (1, 3), la abscisa es el triple de la coordenada.

Pregunta 9. Encuentra la ecuación de una parábola con vértice en el origen, el eje a lo largo del eje x y que pasa por (2, 3).

Solución:

Consideremos la ecuación de la parábola requerida ser,

=> ^y2 = 4ax

Como pasa por (2, 3), obtenemos,

=> 9 = 4a (2)

=> 8a = 9

=> un = 9/8

Entonces, la ecuación es y ² = $\frac{4\left( 9 \right)x}{8}$

es decir, 2y ² = 9x

Supongamos que la ecuación de la parábola requerida sea y ² = -4ax.

Como la ecuación anterior pasa por (2, 3), obtenemos

=> 9 = – 4a (2)

=> 8a = -9

=> un = -9/8

Por lo tanto, la ecuación es,

=> y ² = $\frac{- 4\left( - 9 \right)x}{8}$

=> 2y ² = 9x

Por lo tanto, en cualquier caso, la ecuación requerida de la parábola es 2y ² = 9x.

Pregunta 10. Encuentra la ecuación de una parábola con vértice en el origen y la directriz, y = 2.

Solución:

Dado que, el vértice es (0, 2) y la directriz es y = 2.

Supongamos que (x ₁ , y ₁ ) son las coordenadas del punto de intersección del eje y la directriz.

=> (x ₁ , y ₁ ) = (0, 2)

Supongamos que el foco sea (x ₂ , y ₂ ).

Ahora,

(x ₂ + 0)/2 = 0 y (y ₂ + 2)/2 = 0

=> x2 = ₀ y y2 ₌ -2

Las coordenadas del foco son (0, -2).

Primero dibujamos PM perpendicular a y = 2.

Entonces tenemos:

SP = P.M.

SP ² = PM ²

(x – 0) ² + (y + 2) ² = $\left(\frac{y-2}{\sqrt{1}} \right)^2$

(x – 0) ² + (y + 2) ² = (y – 2) ²

x2 + ^{y2 +}⁴ + 4y = y2 ⁺ 4 – 4y

x2 = ^-4y – 4y

=> x2 = ^-8y

Por lo tanto, la ecuación de la parábola es x ² = -8y.

Publicación traducida automáticamente

Artículo escrito por prabhjotkushparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 11 Soluciones RD Sharma – Capítulo 25 Parábola – Ejercicio 25.1 | Serie 1

Pregunta 1. Encuentra la ecuación de la parábola cuya:

(i) El foco es (3, 0) y la directriz es 3x + 4y = 1

(ii) El foco es (1, 1) y la directriz es x + y + 1 = 0

(iii) El foco es (0, 0) y la directriz 2x − y − 1 = 0

(iv) El foco es (2, 3) y la directriz x − 4y + 3 = 0.

Pregunta 2. Encuentra la ecuación de la parábola cuyo foco es el punto (2, 3) y la directriz es la recta x − 4y + 3 = 0. Además, encuentra la longitud de su lado recto.

Pregunta 3. Encuentra la ecuación de la parábola si

(i) El foco está en (−6, −6) y el vértice está en (−2, 2)

(ii) El foco está en (0, −3) y el vértice está en (0, 0)

(iii) El foco está en (0, −3) y el vértice está en (−1, −3)

(iv) El foco está en (a, 0) y el vértice está en (a’, 0)

(v) El foco está en (0, 0) y el vértice está en la intersección de las líneas x + y = 1 y x − y = 3.

Pregunta 4. Encuentra el vértice, el foco, el eje, la directriz y el latus-rectum de la siguiente parábola:

(i) y ² = 8x

(ii) 4x ² + y = 0

(iii) y ² − 4y − 3x + 1 = 0

(iv) y ² − 4y + 4x = 0

(v) y ² + 4x + 4y − 3 = 0

(vi) ^y2 = 8x + 8y

(vii) 4 (y − 1) ² = − 7 (x − 3)

(viii) y ² = 5x − 4y − 9

(ix) x ² + y = 6x − 14

Pregunta 5. Para la parábola, y ² = 4px encuentra los extremos de una ordenada doble de longitud 8p. Demostrar que las líneas desde el vértice hasta sus extremos son ángulos rectos.

Pregunta 6. Halla el área del triángulo formado por las rectas que unen el vértice de la parábola x ² = 12y con los extremos de su latus rectum.

Pregunta 7. Encuentra las coordenadas del punto de intersección del eje y la directriz de la parábola cuyo foco es (3, 3) y la directriz es 3x − 4y = 2. Encuentra también la longitud del latus-rectum.

Pregunta 8. ¿En qué punto de la parábola x ² = 9y la abscisa es el triple de la coordenada?

Pregunta 9. Encuentra la ecuación de una parábola con vértice en el origen, el eje a lo largo del eje x y que pasa por (2, 3).

Pregunta 10. Encuentra la ecuación de una parábola con vértice en el origen y la directriz, y = 2.

Deja una respuesta Cancelar la respuesta

Pregunta 1. Encuentra la ecuación de la parábola cuya:

(i) El foco es (3, 0) y la directriz es 3x + 4y = 1

(ii) El foco es (1, 1) y la directriz es x + y + 1 = 0

(iii) El foco es (0, 0) y la directriz 2x − y − 1 = 0

(iv) El foco es (2, 3) y la directriz x − 4y + 3 = 0.

Pregunta 2. Encuentra la ecuación de la parábola cuyo foco es el punto (2, 3) y la directriz es la recta x − 4y + 3 = 0. Además, encuentra la longitud de su lado recto.

Pregunta 3. Encuentra la ecuación de la parábola si

(i) El foco está en (−6, −6) y el vértice está en (−2, 2)

(ii) El foco está en (0, −3) y el vértice está en (0, 0)

(iii) El foco está en (0, −3) y el vértice está en (−1, −3)

(iv) El foco está en (a, 0) y el vértice está en (a’, 0)

(v) El foco está en (0, 0) y el vértice está en la intersección de las líneas x + y = 1 y x − y = 3.

Pregunta 4. Encuentra el vértice, el foco, el eje, la directriz y el latus-rectum de la siguiente parábola:

(i) y 2 = 8x

(ii) 4x 2 + y = 0

(iii) y 2 − 4y − 3x + 1 = 0

(iv) y 2 − 4y + 4x = 0

(v) y 2 + 4x + 4y − 3 = 0

(vi) y2 = 8x + 8y

(vii) 4 (y − 1) 2 = − 7 (x − 3)

(viii) y 2 = 5x − 4y − 9

(ix) x 2 + y = 6x − 14

Pregunta 5. Para la parábola, y 2 = 4px encuentra los extremos de una ordenada doble de longitud 8p. Demostrar que las líneas desde el vértice hasta sus extremos son ángulos rectos.

Pregunta 6. Halla el área del triángulo formado por las rectas que unen el vértice de la parábola x 2 = 12y con los extremos de su latus rectum.

Pregunta 7. Encuentra las coordenadas del punto de intersección del eje y la directriz de la parábola cuyo foco es (3, 3) y la directriz es 3x − 4y = 2. Encuentra también la longitud del latus-rectum.

Pregunta 8. ¿En qué punto de la parábola x 2 = 9y la abscisa es el triple de la coordenada?

Pregunta 9. Encuentra la ecuación de una parábola con vértice en el origen, el eje a lo largo del eje x y que pasa por (2, 3).

Pregunta 10. Encuentra la ecuación de una parábola con vértice en el origen y la directriz, y = 2.

Deja una respuesta Cancelar la respuesta

(i) y ² = 8x

(ii) 4x ² + y = 0

(iii) y ² − 4y − 3x + 1 = 0

(iv) y ² − 4y + 4x = 0

(v) y ² + 4x + 4y − 3 = 0

(vi) ^y2 = 8x + 8y

(vii) 4 (y − 1) ² = − 7 (x − 3)

(viii) y ² = 5x − 4y − 9

(ix) x ² + y = 6x − 14

Pregunta 5. Para la parábola, y ² = 4px encuentra los extremos de una ordenada doble de longitud 8p. Demostrar que las líneas desde el vértice hasta sus extremos son ángulos rectos.

Pregunta 6. Halla el área del triángulo formado por las rectas que unen el vértice de la parábola x ² = 12y con los extremos de su latus rectum.

Pregunta 8. ¿En qué punto de la parábola x ² = 9y la abscisa es el triple de la coordenada?