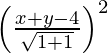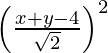Clase 11 Soluciones RD Sharma – Capítulo 25 Parábola – Ejercicio 25.2

Pregunta 1. Encuentra el eje de simetría de la parábola y ² = x.

Solución:

Se nos da,

=> y ² = x

Sabemos que esta parábola se encuentra en el eje y.

Por lo tanto, su vértice se encuentra en el eje y.

Ahora sabemos que la parábola siempre tiene un eje que mantiene su simetría.

En este caso, el eje es un eje x, que divide la parábola en dos partes iguales.

Por lo tanto, el eje requerido es el eje x.

Pregunta 2. Encuentra la distancia entre el vértice y el foco de la parábola y ² + 6y + 2x + 5 = 0.

Solución:

Dado que,

y ² + 6y + 2x + 5 = 0

(y + 3) ² + 2x – 4 = 0

(y + 3) ² = -2 (x – 2)

Supongamos que Y = y + 3 y X = x – 2.

De la ecuación obtenemos,

Y ² = – 2X

Al poner 4a = 2, obtenemos

=> un = 1/2

Enfoque = (X = -1/2, Y = 0) = (x = 3/2, y = -3)

Vértice = (X = 0, Y = 0) = (x = 2, y = -3)

Así, obtenemos

Enfoque = (3/2, -3)

Vértice = (2, -3)

La distancia entre el vértice y el foco es,

re = $\sqrt{\left( \frac{3}{2} - 2 \right)^2 + \left( - 3 + 3 \right)^2}$

= $\sqrt{\left( \frac{1}{2} \right)^2}$

= 1/2 unidades

Por lo tanto, la distancia requerida es 1/2 unidades.

Pregunta 3. Encuentra la ecuación de la directriz de la parábola x ² − 4x − 8y + 12 = 0.

Solución:

Dado que,

x2 − 4x − 8y + 12 = ⁰

(x – 2) ² – 4 – 8y + 12 = 0

(x-2) ² = 8 (y-1)

Sean Y = y − 1 y X = x – 2.

De la ecuación anterior, obtenemos,

X2 ⁼ 8Y

Al comparar con x ² = 4ay, obtenemos

=> un = 2

Directriz = Y = −a

=> y − 1 = −a

=> y = −a + 1

=> y = −2 + 1

=> y = −1

Por lo tanto, la ecuación de la directriz es y = -1.

Pregunta 4. Escribe la ecuación de la parábola con foco (0, 0) y directriz x + y − 4 = 0.

Solución:

Supongamos que P (x, y) es cualquier punto de la parábola cuyo foco es S (0, 0).

Y la ecuación de la directriz es x + y= 4.

Primero dibujamos PM perpendicular a x + y = 4.

Entonces tenemos,

SP = P.M.

SP ² = PM ²

(x – 0) ² + (y – 0) ² = $\left( \frac{x + y - 4}{\sqrt{1 + 1}} \right)^2$

x ² + y ² = $\left( \frac{x + y - 4}{\sqrt{2}} \right)^2$

2x ² + 2y ² = x ² + y ² + 16 + 2xy – 8y – 8x

=> x2 + ^{y2 –}^2xy + 8x + 8y – 16 = 0

Por lo tanto, la ecuación de la parábola es x ² + y ² – 2xy + 8x + 8y – 16 = 0

Pregunta 5. Encuentra la longitud de la cuerda de la parábola y ² = 4ax que pasa por el vértice y está inclinada respecto al eje en π/4.

Solución:

Consideremos que OP es la cuerda y las coordenadas de P son (x ₁ , y ₁ ).

Tenemos,

=> PO ² = x ₁² + y ₁²

Y, tan π/4 = y ₁ /x ₁

=> 1 = _y1_/ x1

=> _x1 = _y1

y (x ₁ , y ₁ ) se encuentra en la parábola.

∴ y ₁² = 4ax ₁

Entonces, obtenemos

=> x ₁² = 4a x ₁

=> x1 ₌ 4a

Por lo tanto, tenemos

OP ² = (4a) ² + (4a) ²

OP ² = 32a ²

OP = 4√2a

Por lo tanto, la longitud de la cuerda es 4√2 a.

Pregunta 6. Si b y c son las longitudes de los segmentos de cualquier cuerda focal de la parábola y ² = 4ax, entonces escribe la longitud de su latus-rectum.

Solución:

Supongamos que S (a, 0) sea el foco de la parábola dada y que los puntos finales de la cuerda focal sean P(at ² , 2at) y Q (a/t ² }, -2a/t).

Ahora, SP y SQ son segmentos de la cuerda focal con longitudes b y c.

∴ SP = b, SQ = c

Además, SP = $\sqrt{\left( a - a t^2 \right) + 4 a^2 t^2}$

= un (1 + t ² )

Y, SQ = $\sqrt{\left( a - \frac{a}{t^2} \right) + \frac{4 a^2}{t^2}}$

= a (1 + 1/t ² )

Ahora, obtenemos,

$\frac{1}{SP} + \frac{1}{SQ} = \frac{1}{a\left( 1 + t^2 \right)} + \frac{t^2}{a\left( 1 + t^2 \right)}$

$\frac{1}{SP} + \frac{1}{SQ} = \frac{1}{a}$

$\frac{1}{b} + \frac{1}{c} = \frac{1}{a}$

$\frac{b + c}{bc} = \frac{1}{a}$

=> un = $\frac{bc}{b + c}$

Por lo tantoc, la longitud del latus rectum es 4a = $\frac{4bc}{b + c}$

Pregunta 7. PSQ es una cuerda focal de la parábola y ² = 8x. Si SP = 6, entonces encuentre SQ.

Solución:

De acuerdo a la pregunta se da que PSQ es una cuerda focal de la parábola y ² = 8x y SP = 6

Entonces, las coordenadas de la cuerda focal son P (en ² , 2 en) y Q (a/t ² , – 2a/t).

Al comparar y ² = 8x con y ² = 4ax, obtenemos,

=> 4a = 8

=> un = 2

Por lo tanto, las coordenadas del foco S son (2, 0).

SP = 6

$\sqrt{\left( 2 - 2 t^2 \right)^2 + \left( 4t \right)^2} = 6$

t ⁴ + 2 t ² – 8 = 0

=> t ² = 2

Así, obtenemos,

SQ = $\sqrt{\left( 2 - \frac{2}{t^2} \right)^2 + \left( \frac{4}{t^2} \right)}$

= $\sqrt{\left( 2 - \frac{2}{2} \right)^2 + \left( \frac{4}{2} \right)}$

= $\sqrt{(1)^2 +(2)^2}$

= √5

Por lo tanto, SQ es √5.

Pregunta 8. Escribe las coordenadas del vértice de la parábola cuyo foco está en (−2, 1) y la directriz es la recta x + y − 3 = 0.

Solución:

Dado que, el foco S está en (−2, 1) y la directriz es la recta x + y − 3 = 0 y la pendiente de la recta perpendicular a x + y − 3 = 0 es 1.

Ahora, el eje de la parábola es perpendicular a la directriz y pasa por el foco.

Entonces, la ecuación del eje de la parábola se convierte en,

=> y – 1 = 1 (x + 2)

Ahora, el punto de intersección de la directriz y el eje es el punto de intersección de la parábola y x + y − 3 = 0.

Supongamos que el punto de intersección sea K.

Entonces, las coordenadas de K son (0, 3).

Supongamos que el punto (h, k) son las coordenadas del vértice, que es el punto medio del segmento de recta que une K y el foco.

=> h = (0 – 2)/2, k = (3 + 1)/2

=> h = -1, k = 2

Por lo tanto, las coordenadas del vértice son (−1, 2).

Pregunta 9. Si las coordenadas del vértice y el foco de una parábola son (−1, 1) y (2, 3) respectivamente, entonces escribe la ecuación de su directriz.

Solución:

Dado que, el vértice y el foco de una parábola son (−1, 1) y (2, 3).

Entonces, la pendiente del eje de la parábola = $\frac{3 - 1}{2 + 1}$ = 2/3

Pendiente de la directriz = -3/2

Supongamos que la directriz corta el eje en el punto K (r, s).

Entonces, (r + 2)/2 = -1, (s + 3)/2 = 1

=> r = -4, s = -1

Ahora, la ecuación requerida de la directriz es,

y + 1 = (-3/2) (x + 4)

=> 3x + 2y + 14 = 0

Pregunta 10. Si la parábola y ² = 4ax pasa por el punto (3, 2), entonces encuentra la longitud de su lado recto.

Solución:

Dado que, y ² = 4ax y la parábola pasa por el punto (3, 2)

Entonces, esto satisfará la ecuación de la parábola.

22 = 4(a)(3)

=> un = 1/3

La longitud del latus ractum = 4a

= 4 (1/3)

= 4/3

Por lo tanto, el latus ractum es 4/3

Pregunta 11. Escribe la ecuación de la parábola cuyo vértice está en (−3, 0) y la directriz es x + 5 = 0.

Solución:

Dado que el vértice (h, k) es (-3, 0) y la directriz es x + 5 = 0

Entonces, la ecuación general de la parábola = (y − k) ² = 4a (x − h).

Ahora, la directriz es

x = h – un

Como x + 5 = 0, obtenemos

=> −5 = −3 − un

=> un = 2

Entonces, la ecuación de la parábola es

(y – 0) ² = 4 (2) (x + 3)

=> y ² = 8 (x + 3)

Publicación traducida automáticamente

Artículo escrito por prabhjotkushparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1. Encuentra el eje de simetría de la parábola y 2 = x.

Pregunta 2. Encuentra la distancia entre el vértice y el foco de la parábola y 2 + 6y + 2x + 5 = 0.

Pregunta 3. Encuentra la ecuación de la directriz de la parábola x 2 − 4x − 8y + 12 = 0.

Pregunta 4. Escribe la ecuación de la parábola con foco (0, 0) y directriz x + y − 4 = 0.

Pregunta 5. Encuentra la longitud de la cuerda de la parábola y 2 = 4ax que pasa por el vértice y está inclinada respecto al eje en π/4.

Pregunta 6. Si b y c son las longitudes de los segmentos de cualquier cuerda focal de la parábola y 2 = 4ax, entonces escribe la longitud de su latus-rectum.

Pregunta 7. PSQ es una cuerda focal de la parábola y 2 = 8x. Si SP = 6, entonces encuentre SQ.

Pregunta 8. Escribe las coordenadas del vértice de la parábola cuyo foco está en (−2, 1) y la directriz es la recta x + y − 3 = 0.

Pregunta 9. Si las coordenadas del vértice y el foco de una parábola son (−1, 1) y (2, 3) respectivamente, entonces escribe la ecuación de su directriz.

Pregunta 10. Si la parábola y 2 = 4ax pasa por el punto (3, 2), entonces encuentra la longitud de su lado recto.

Pregunta 11. Escribe la ecuación de la parábola cuyo vértice está en (−3, 0) y la directriz es x + 5 = 0.

Deja una respuesta Cancelar la respuesta

Pregunta 1. Encuentra el eje de simetría de la parábola y ² = x.

Pregunta 2. Encuentra la distancia entre el vértice y el foco de la parábola y ² + 6y + 2x + 5 = 0.

Pregunta 3. Encuentra la ecuación de la directriz de la parábola x ² − 4x − 8y + 12 = 0.

Pregunta 5. Encuentra la longitud de la cuerda de la parábola y ² = 4ax que pasa por el vértice y está inclinada respecto al eje en π/4.

Pregunta 6. Si b y c son las longitudes de los segmentos de cualquier cuerda focal de la parábola y ² = 4ax, entonces escribe la longitud de su latus-rectum.

Pregunta 7. PSQ es una cuerda focal de la parábola y ² = 8x. Si SP = 6, entonces encuentre SQ.

Pregunta 10. Si la parábola y ² = 4ax pasa por el punto (3, 2), entonces encuentra la longitud de su lado recto.